(1)
| Реферат | Библиотека | Ссылки | Биография | Индивидуальное задание |
Выполнил:
Ст. гр. СУА-06м
Титков С.Ю.
По мере развития машиностроения, прежде всего, автоматизировались наиболее сложные и трудоемкие операции, связанные с изменениями формы и размеров изделий. Загрузка и разгрузка технологического оборудования осуществлялась обычно вручную или простейшими средствами механизации. В последнее время большое внимание уделяется автоматизации операций манипулирования - перемещения и ориентации изделий и инструмента
Современное автоматизированное сборочное оборудование (АСО) представляет собой комплекс сложных динамических систем. Сложность их обусловлена высокими требованиями к производительности и точности работы сборочного оборудования, а также разнообразием выполняемых им функций. Одним из важнейших вопросов, которые необходимо решать при проектировании и эксплуатации таких следящих систем, является вопрос об устойчивости системы. Другой не менее важный вопрос разработки - это обеспечения безскачкообразного режима работы системы и плавности переходных процессов с системе управления.
В данной работе рассматриваются вопросы синтеза законов управления, дающих возможность на базе построенных динамических моделей осуществлять эффективное управление манипулятором. Это обусловлено тем, что в основу современных методов управления положены математическая теория оптимальных процессов, теория пространства состояния и модальное управление. Применение методов пространства состояний дискретных динамических систем для математического описания манипулятора является более предпочтительным в сравнении с методами управления непрерывных систем, так как реальное управление любым манипулятором осуществляется с помощью цифровой ЭВМ. В связи с этим, рассмотрение динамики манипулятора в дискретном времени позволяет избежать ошибок, связанных с квантованием сигналов в АЦП.
Для описания дискретной следящей системы шарнира манипулятора в пространстве параметров состояний задается математическая модель в виде системы векторно-матричных уравнений:
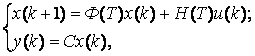(1)
где x(k) - вектор состояния;
u(k) - вектор управления;
Ф(T) - матрица перехода состояния дискретной системы;
Н(Т) - вектор управляемого перехода дискретной системы;
Т - период дискретизации.
Задача аналитического конструирования регулятора для дискретного объекта управления заключается в выборе структуры и параметров регулятора, вырабатывающего управление u(k). Данное управление обеспечивает проектируемой системе требуемую совокупность показателей качества:
(2)
где К - матрица линейных стационарных ОС по состояниям ОУ;
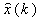- вектор оценки переменных состояния системы.
Для нахождения матрицы К по заданным значениям переходного процесса tп и перерегулированию δ назначена эталонная модель в виде динамической системы:
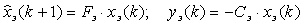(3)
где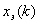 
- вектор состояния эталонной модели;
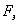- переходная матрица эталонной модели;
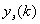- вектор выхода эталонной модели;
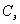- матрица выхода эталонной модели.
Заданием матрицы 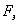определяются желаемые полюса замкнутой системы. Эти полюса удовлетворяют характеристическому уравнению переходной матрицы эталонной модели.
Для синтеза модального регулятора задана эталонная модель с биноминальным распределением корней характеристического уравнения, поскольку желаемый переходный процесс в этом случае протекает без перерегулирования:
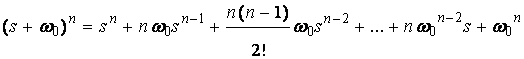(4)
где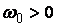 
- изменяемый параметр, который выбирают исходя из заданного времени переходного процесса.
Стандартный полином определяет характеристическое уравнение матрицы 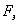, то есть
(5)
Для задания матриц 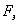использована каноническая форма в виде матрицы Фробениуса.
Матрица линейных стационарных ОС по состояниям ОУ равна:
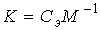(6)
Алгебраическое матричное уравнение:
(7)
Решив относительно М уравнение (6), получены выражения:
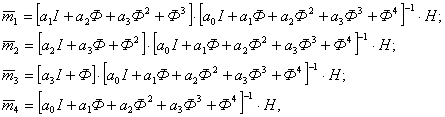(8)
где 
- векторы, содержащие столбцы матрицы М.
Регулятор, вырабатывающий закон управления (2), является динамическим регулятором, так как в его структуру входит модальный регулятор и дополнительное динамическое звено – эстиматор состояния.
Поскольку в данной следящей системе одна из компонент вектора состояния измерима и известна, то оставшиеся переменные состояния восстанавливаются с помощью синтезированного эстиматора состояния пониженного порядка. В общем случае векторно-матричное уравнение динамики эстиматора имеет вид:
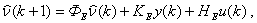(9)
где 
В результате выполнения данной работы:
Получены уравнения движения электропривода шарнира манипулятора сборочного робота;
Синтезирован модальный регулятор на основе желаемых полюсов, заданных с помощью биномиального закона распределения корней;
Получен алгоритм работы эстиматора состояния для восстановления неизмеряемых координат;
На основе синтезированных модального регулятора и эстиматора состояния разработан динамический регулятор, обеспечивающий заданные показатели качества следящей системы управления шарниром манипулятора сборочного робота.
| Реферат | Библиотека | Ссылки | Биография | Индивидуальное задание |