(1)
| Реферат | Библиотека | Ссылки | Биография | Индивидуальное задание |
АКОР в России впервые был разработан профессором Летовым. Заслуга профессора Летова состоит в том , что он процесс синтеза оптимального управления поставил на математическую основу выраженную в аналитической форме. Для этого профессор Летов обоснованно в своем методе выбирал критерий оптимальности и на основании математической модели объекта управления и выбранного критерия оптимальности аналитически находил выражение для алгоритма оптимального управления или выражение для оптимального регулятора. Одновременно с профессором Летовым америк. математиком Калманом был разработан метод подобный АКОРу , который назывался Метод пространства состояния, который явился основой современной теории управления. Заслуга Калмана состоит в том , что он разработал методы синтеза алгоритма оптимального управления, не только для детерминированной динамической системы , но и для стохастических динамических систем (со случайным переходным процессом).
(1)
где
– матрица коэффициентов объекта управления,
коэффициенты зависят от времени;
- прямоугольная матрица распределения управляющих воздействий. Коэффициенты этой матрицы также зависят от времени;
- n-мерный вектор состояния;
- m-мерный вектор управления.
(2)
- p-мерный вектор выхода;
- матрица выхода динамической системы коэффициентов, которые зависят от времени.
В постановке задачи АКОР очень важное место занимает выбор критерия оптимальности или выбор функционала качества.
В общем случае для обоснованного выбора критерия оптимальности выбирается
желаемый вектор выходных координат 
, задача АКОР
состоит в том, чтобы текущее значение выхода вектора было близко к желаемому:
(3)
Мы хотим чтобы в 
, при 
, 
В этом случае, учитывая рассуждения критерия оптимальности в общем виде можно представить так:
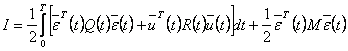(4)
Задача АКОР с критерия вида (4) называется задачей слежения, текущая выходная
координата отслеживания желаемых выходных координат.
Физический смысл слагаемых:
1-ое слагаемое представляет собой просуммированную ошибку и в этом слагаемом матрица Q(t) это матрица квадратичной формы 
. Весовые коэффициенты этой матрицы выбираются с тем расчетом чтобы в конечном итоге первое слагаемое имело минимальное значение.
1-ое слагаемое характеризует точность работы системы.
2-ое слагаемое - квадратичная форма. физически характеризует затраты энергии на управление, косвенным образом это слагаемое характеризует и быстродействие системы ,чем больше затраты энергии на
управление, тем более быстродейственнее является система. Выбирая компромисс между затратами энергии на управление и полученным быстродействием:
Второй случай решения задачи АКОР.
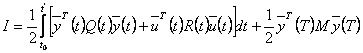(5)
Целью управления является удержание выходных координат объекта
Если начальное отклонение выходных координат относительно 0 велико, то управляющее устройство должно в начале выходные координаты приблизить к нулю, а затем удерживать их около нуля, при этом не расходуя много энергии на управление.Подобную задачу называют задачей о рег. выхода
Рассмотрим третий случай
Третий случай решения задачи Акор связано с задачей удержания около нуля не выходного вектора и его компонентов, а компонентов вектора состояния.
Критерий оптимальности будет выглядеть следующим образом
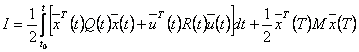(6)
В этом случае оптимальное управление должно минимизировать критерий вида, а соответственно задачу называют задачей о регуляторе состояния.
Четвертый случай.
Во всех трех случаях предполагается , что матрицы A(t), B(t), Q(t), R(t)– зависят от времени.
(7)
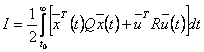(8)
Второй особенностью четвертого случая является то , что верхний предел интеграла имеет бесконечность. При этом М=0. Предполагая при этом, что на вектор управления U(t) не наложено никаких ограничений.
(9)
Выражение (9) эквивалентно асимптотической устойчивости синтезированной системы. В четвертом случае задача сводится к поиску такого вектора управления 
под действием кот. критерий вида (8) достигает min значения и при этом выполняется условие асимптотической устойчивости.
Кроме рассмотренных 4-х случаев на практике встречаются задачи с оптимизацией нелинейных объектов и с ограничением на управляющее воздействие.
В этом случае решение задачи Акор осуществляется на основе принципа Понтрягина, кот. приспособлен специально для решения подобного рода задач, т.е. для решения задач оптимизации с нелинейным объектом и с ограничением на управляющее воздействие и фазовые координаты.
| Реферат | Библиотека | Ссылки | Биография | Индивидуальное задание |