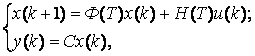(1)
| Реферат | Библиотека | Ссылки | Биография | Индивидуальное задание |
Тезисы к докладу на международную конференцию "Автоматика - 2007",
которая состоится в г.Севастополь в сентябре 2007г.
Авторы:
Титков Сергей Юрьевич, ст. гр СУА-06м, ДонНТУ.
Рафиков Гыяз Шагиевич, к.т.н., доц. кафедры АТ ДонНТУ
Для выполнения опасных, однообразных простых или шаблонных операций при сборке бытового или промышленного оборудования особую важность приобретают автоматические устройства. Машины для автоматической сборки позволяют повысить точность сборки, безопасность, экономичность и производительность труда.
Современное автоматизированное сборочное оборудование (АСО) представляет собой комплекс сложных динамических систем. Сложность их обусловлена высокими требованиями к производительности и точности работы сборочного оборудования, а также разнообразием выполняемых им функций. Одним из важнейших вопросов, которые необходимо решать при проектировании и эксплуатации таких следящих систем, является вопрос об устойчивости системы. Другой не менее важный вопрос разработки - это обеспечение безскачкообразного режима работы системы и плавности переходных процессов в системе управления.
Добиться эффективного управления манипулятором сборочного робота позволяет использование в качестве математического аппарата управления современных методов теории управления – теории пространства состояний,теории оптимальных процессов и модального управления. Поскольку реальное управление манипулятором осуществляется с помощью цифровой ЭВМ дискретным способом, то использование методов пространства состояний для дискретных динамических систем является более предпочтительным, чем для непрерывных.Таким образом, рассмотрение динамики манипулятора в дискретном времени позволяет избежать ошибок, связанных с квантованием сигналов в аналогово-цифровых преобразователях, включаемых в систему управления.
Для описания дискретной следящей системы шарнира манипулятора в пространстве параметров состояний задается математическая модель в виде системы векторно-матричных уравнений:
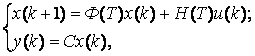(1)
где x(k) - вектор состояния;
u(k) - вектор управления;
Ф(T) - матрица перехода состояния дискретной системы;
Н(Т) - вектор управляемого перехода дискретной системы;
Т - период дискретизации.
Поскольку текущее значение вектора состояния x(k) объекта управления, дает полную информацию об объекте управления и внешних воздействиях в данный момент времени и включает в себя предысторию о поведении в прошлом, поэтому закон управления, вырабатываемый регулятором является функцией состояния ОУ. Если все переменные вектора состояния ОУ доступны для измерения, то говорят об объекте управления с полной информацией. В этом случае регулятор вырабатывает закон управления как линейную функцию состояний:
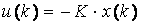(2)
где К - матрица линейных стационарных обратных связей (ЛСОС) по состояниям ОУ размерности (m x n).
В реальных условиях не все компоненты вектора состояний измеримы. В этом случае располагают объектом управления с неполной информацией и для реализации закона управления используют оценки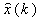 
состояний ОУ и закон управления в этом случае приобретает вид:
(3)
где 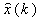- оценки вектора состояния.
Задача синтеза регулятора для дискретной системы вида (1) заключается в выборе структуры и параметров регулятора, который по информации, поступающей от измерителя состояния вырабатывает управление u(k). Это управление обеспечивает системе требуемую совокупность показателей качества, таких как: время переходного процесса tп, время нарастания переходного процесса tн, перерегулирование δ и др.
Под модальным управлением понимается изменение собственных движений замкнутой системы, а следовательно и полюсов системы с помощью управляющих воздействий с целью достижения требуемых показателей качества. При модальном синтезе проектируется ООС по переменным состояния таким образом, чтобы полюса системы находились в наперед заданной области и их расположение определяло бы необходимое качество управления. Связь полюсов замкнутой системы с требуемыми показателями качества основывается на использовании стандартных полиномов, определяющих коэффициенты характеристического уравнения проектируемой системы. Стандартные полиномы задают эталонную модель системы, обладающую желаемыми показателями качества. Поэтому синтез регуляторов с помощью метода модальных управлений состоит в задании эталонной модели с желаемыми свойствами и нахождении матрицы ЛСОС по состояниям ОУ - закона управления, обеспечивающего в замкнутой системе те же самые полюса, что и в эталонной модели:
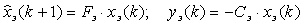(4)
где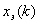 
- вектор состояния эталонной модели;
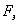- переходная матрица эталонной модели;
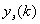- вектор выхода эталонной модели;
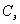- матрица выхода эталонной модели.
Для синтеза модального регулятора задана эталонная модель с биноминальным распределением корней характеристического уравнения, поскольку желаемый переходный процесс в этом случае протекает без перерегулирования:
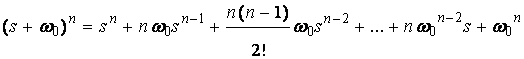(5)
где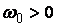 
- изменяемый параметр, который выбирают исходя из заданного времени переходного процесса.
Регулятор, вырабатывающий закон управления (3), является динамическим регулятором, так как в его структуру входит модальный регулятор и дополнительное динамическое звено – эстиматор состояния (наблюдатель состояния полного или пониженного порядка).
Поскольку в данной следящей системе одна из компонент вектора состояния измерима и известна, то оставшиеся переменные состояния восстанавливаются с помощью синтезированного эстиматора состояния пониженного порядка. В общем случае векторно-матричное уравнение динамики эстиматора имеет вид:
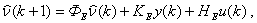(6)
где 
Уравнение эстиматора найдено по желаемому расположению его корней. Они выбраны равными нулю из тех соображений, что при таких корнях эстиматор является достаточно быстродействующим и позволяет восстанавливать переменные состояния с достаточной точностью за время равное 3..5 интервалам дискретности обьекта управления.
В данной работе проведен анализ следящей системы с динамическим регулятором путем оценки поведения выходной координаты системы – угла поворота звена манипулятора, при отклонении некоторых параметров системы от расчетных значений. При изменении момента инерции, коэфициента вязкого трения и периода дискретности системы в интервале от -50% до +50% статическая ошибка, время регулирования и время перерегулирования не превышают заданных значений.
| Реферат | Библиотека | Ссылки | Биография | Индивидуальное задание |