Реферат

Библиотека

Ссылки

Биография

Индивидуальное задание

Рафиков Г.Ш. Цифровые системы управления. Конспект лекций. – Донецк 1999 г.

6.2 Синтез модального регулятора дискретной динамической системы на основе метода Аккермана

        Пусть задано уравнение состояния дискретной динамической системы вида:

 ,                                                                                          (6.12)

        а уравнение управления задано в виде:

.                                                                                                   (6.13)

        Подстановка уравнения (6.13) в (6.12) дает:

.                                                                                          (6.14)

        Введем обозначение:

,                                                                                                   (6.15)

        где - матрица перехода состояний замкнутой системы.

        Желаемое характеристическое уравнение, получаемое в результате желаемого размещения полюсов замкнутой системы на Z-плоскости, имеет вид:

                                            (6.16)

        где  - собственные числа замкнутой системы, произвольным образом размещенные на Z-плоскости;

         - коэффициенты характеристического уравнения замкнутой системы.

        Далее введем в рассмотрение характеристический полином замкнутой дискретной системы  и полиномиальную матрицу

;                                                                                          (6.17)

.                                                                           (6.18)

        Теорема Кейли-Гамильтона утверждает, что матрица удовлетворяет своему собственному характеристическому уравнению, поэтому запишем:

.                                                                           (6.19)

        В дальнейшем используем уравнение (6.19) для того, чтобы вывести формулу Аккермана.

        Чтобы упростить вывод формулы Аккермана, рассмотрим случай, когда . (Для другого положительного целого числа n проведение вывода может быть легко обобщено).

        Рассмотрим следующие тождества:

;                                                      (6.20)

.

        Умножение этих уравнений на  соответственно и последующее сложение полиномов дает нам следующее:

.                                                        (6.21)

        Что касается уравнения (6.19), мы имеем:

.                                                                                   (6.22)

        Также, мы имеем:

.                                                                                      (6.23)

        При подстановке последних двух уравнений в уравнение (6.21), получим:

.                                             (6.24)

        Поскольку , то получим:

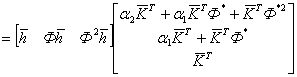.                                                                                       (6.25)

        Так как  и система вполне управляема, то обратная матрица достижимости существует и может быть записана в виде:

.

        Домножив обе части уравнения (6.25) слева на обратную матрицу достижимости, получим:

;                                                                           (6.25)

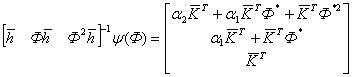.                                                                            (6.26)

        Наконец, умножив обе части этого уравнения слева на вектор , получим:

.                                              (6.27)

        Выражение (6.27) может быть переписано следующим образом:

.                                                                                           (6.28)

        Последнее выражение определяет требуемую матрицу обратной связи по состоянию .

        Для произвольного положительного целого числа n можно получить подобное выражение для обратной связи по состоянию:

,                                             (6.29)

        где .

.                                                                           (6.30)

        Уравнение (6.29) известно как формула Аккермана для определения матрицы обратной связи по состоянию.
        Выводы по синтезу модального регулятора на основе желаемого размещения полюсов замкнутой системы.
        Матрица обратных связей по состоянию определена таким образом, что ошибка, вызванная погрешностями, уменьшается до нуля достаточно быстро. Следует иметь в виду, что матрица не однозначна для данной системы и зависит от желаемого положения выбранных полюсов замкнутой системы (которые определяют быстродействие). Выбор желаемых полюсов замкнутой системы или желаемого характеристического уравнения – компромисс между быстротой реакции вектора ошибки и чувствительностью к шумам и помехам. То есть, если мы увеличиваем быстродействие ответа ошибки, влияние помех  и шумов увеличивается. При определении матрицы  для данной системы исследуют отдельные матрицы , образованные из различных желаемых характеристических уравнений и выбирают ту, которая обуславливает высокую эффективность системы.

1. Рафиков Г.Ш. Цифровые системы управления. Конспект лекций. – Донецк 1999 г.

Реферат

Библиотека

Ссылки

Биография

Индивидуальное задание