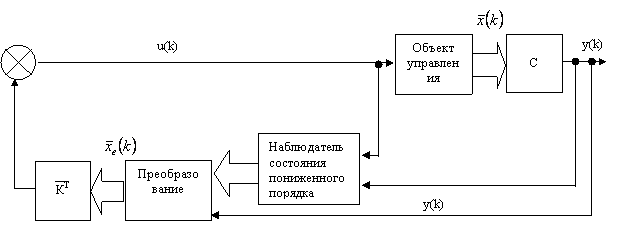
 Рисунок 1 - Линейная дискретная система с наблюдателем пониженного порядка
Рисунок 1 - Линейная дискретная система с наблюдателем пониженного порядка
| Реферат | Библиотека | Ссылки | Биография | Индивидуальное задание |
Наблюдатели, рассмотренные до сих пор, разработаны для того чтобы восстанавливать все переменные состояния. Однако в реальных условиях некоторые из переменных состояния могут не оцениваться.
Наблюдатель, который оценивает меньше, чем n переменных состояния, где n размерность вектора состояния называется наблюдателем состояния пониженного порядка (или просто наблюдателем пониженного порядка). Если порядок наблюдателя пониженного порядка минимально возможный, то такой наблюдатель называется наблюдателем состояния минимального порядка (или наблюдатель с минимальным порядком).
 Рисунок 1 - Линейная дискретная система с наблюдателем пониженного порядка
Рисунок 1 - Линейная дискретная система с наблюдателем пониженного порядка
Предположим, что вектор состояния является n-мерным вектором, а вектор выхода ![]() - m-мерным вектором, который может измеряться. Поскольку m выходных переменных являются линейной комбинацией переменных состояния, то m переменных состояния могут не оцениваться. Должно оцениваться только
- m-мерным вектором, который может измеряться. Поскольку m выходных переменных являются линейной комбинацией переменных состояния, то m переменных состояния могут не оцениваться. Должно оцениваться только ![]() переменных состояния. По этой причине наблюдатель приведенного порядка становится наблюдателем
переменных состояния. По этой причине наблюдатель приведенного порядка становится наблюдателем ![]() -порядка. Такой наблюдатель
-порядка. Такой наблюдатель ![]() - порядка является наблюдателем минимального порядка. Рис.1 иллюстрирует блок-схему системы с наблюдателем минимального порядка.
- порядка является наблюдателем минимального порядка. Рис.1 иллюстрирует блок-схему системы с наблюдателем минимального порядка.
Важно отметить, однако, что если измерение переменных выхода включает значительные шумы и относительные
неточности, то использование наблюдателя состояния полного порядка может приводить к лучшей эффективности системы.
Наблюдатель минимального порядка может быть получен путем разделения вектора состояния ![]() на две части следующим образом:
на две части следующим образом:
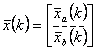 ,
(12.1)
,
(12.1)
где ![]() - та часть вектора состояния, которая может непосредственно измеряться, т.е.
- та часть вектора состояния, которая может непосредственно измеряться, т.е. ![]() - это
m-мерный вектор;
- это
m-мерный вектор;
![]() - не измеряемая часть вектора состояния, т.е.
- не измеряемая часть вектора состояния, т.е. ![]() - это
- это ![]() -мерный вектор.
-мерный вектор.
Тогда разбитые на блоки уравнения состояния и выхода могут быть представлены в следующем виде
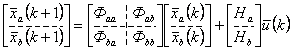 ,
(12.2)
,
(12.2)
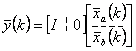 ,
(12.3)
,
(12.3)
где Фaa- ![]() матрица;
матрица;
Фab - ![]() матрица;
матрица;
Фba - ![]() матрица;
матрица;
Фbb - ![]() матрица.
матрица.
![]() -
- ![]() матрица;
матрица;
![]() -
- ![]() матрица.
матрица.
Представим каждое из уравнений (12.2) и (12.3) в виде двух уравнений: уравнения измеряемой части и уравнения не измеряемой части.
Уравнение для измеряемой части состояния будет иметь вид
![]()
![]() ,
(12.4)
,
(12.4)
где компоненты левой части уравнения (12.4) – могут измеряться. Уравнение (12.4) – это уравнение выходного сигнала. При синтезе наблюдателя минимального порядка левую часть уравнения (12.4) рассматриваем как известные величины. Фактически, уравнение (12.4) связывает измеримые величины и неизмеримые величины состояния.
Из уравнения (12.2) уравнение для не измеряемой части вектора состояния можно представить в следующем виде
![]() .
(12.5)
.
(12.5)
Уравнение (12.5) описывает динамику не измеряемой части вектора состояния. Следует обратить внимание на то, что
![]() и
и ![]() - известные векторные величины.
- известные векторные величины.
Синтез матрицы обратной связи для наблюдателя с минимальным порядком можно значительно упростить, если использовать метод синтеза, разработанный для наблюдателя состояния полного порядка.
Сравним уравнение состояния для наблюдателя состояния полного порядка с «уравнением состояния» для наблюдателя минимального порядка
![]() .
(12.6)
.
(12.6)
Уравнение состояния для наблюдателей минимального порядка
![]() .
(12.7)
.
(12.7)
Уравнение выхода для наблюдателя полного порядка
![]() .
(12.8)
.
(12.8)
Уравнение выхода для наблюдателя минимального порядка
![]() .
(12.9)
.
(12.9)
Введем в рассмотрение список необходимых замен для записи уравнения наблюдателя состояния минимального порядка и представим его в виде таблицы.
Таблица 12.1
|
Наблюдатель состояния полного порядка |
Наблюдатель состояния минимального порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
Синтез наблюдателя состояния минимального порядка может выполняться подстановкой параметров из табл. 12.1 в уравнение наблюдателя полного порядка вида
![]() .
(12.10)
.
(12.10)
Произведя подстановку из таблицы 12.1 в уравнение (12.10), получим
![]() ,
(12.11)
,
(12.11)
где ![]() - матрица обратной связи размерности
- матрица обратной связи размерности ![]() .
.
Что касается уравнения (12.3), то имеем такое равенство
![]() .
(12.12)
.
(12.12)
Подставляя уравнение (12.12) в (12.11) получим
![]() .
(12.13)
.
(12.13)
Следует обратить внимание на то, что при оценке вектора ![]() возникает необходимость в измерении вектора
возникает необходимость в измерении вектора ![]() . Это очень неудобно, так как необходимо измерения производить на один шаг вперед.
. Это очень неудобно, так как необходимо измерения производить на один шаг вперед.
Однако это неудобство легко устраняется, т. к. в случае наблюдателя состояния полного порядка, вектор ![]() можно оценить, используя измерения
можно оценить, используя измерения ![]() и не требуя измерения
и не требуя измерения ![]() (см. уравнение (12.10)).
(см. уравнение (12.10)).
Представим уравнение (12.13) в следующем виде:
![]()
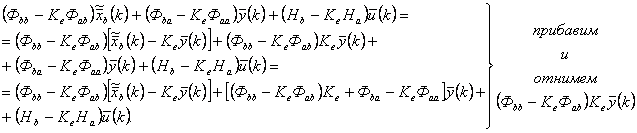
Введем обозначения:
![]() ,
(12.15)
,
(12.15)
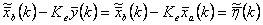 .
(12.16)
.
(12.16)
С учетом введенных обозначений уравнение (12.14) можно представить следующим образом:
![]() .
(12.17)
.
(12.17)
Уравнения (12.15), (12.16) и (12.17) определяют динамику наблюдателя минимального порядка. Следует обратить внимание на то, что для получения ![]() отпадает необходимость в измерении вектора
отпадает необходимость в измерении вектора ![]() .
.
Далее вычитая уравнение (12.16) из уравнения (12.15), получим вектор ошибки ![]() который равен:
который равен:
![]() .
(12.18)
.
(12.18)
При вычитании уравнения (12.11) из уравнения (12.5) получим
![]() .
(12.19)
.
(12.19)
Подставляя уравнение (12.4) в уравнение (12.19), получим:
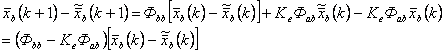 .
(12.20)
.
(12.20)
С учетом введенных обозначений (12.18) уравнение (12.20) можно представить в упрощенном и компактном виде
![]() .
(12.21)
.
(12.21)
Это уравнение вектора ошибки наблюдателя состояния минимального порядка. Следует обратить внимание на то, что вектор ошибки ![]() является
является ![]() -мерным вектором.
-мерным вектором.
Динамическая ошибка может быть определена методикой, разработанной для наблюдателя состояния полного порядка, если ранг матрицы наблюдаемости равен ![]() .
.
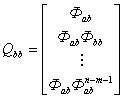 .
(12.22)
.
(12.22)
Эти условия полной наблюдаемости применимы и к наблюдателю состояния минимального порядка, полученного из уравнения (12.21) следующим образом:
![]() .
(12.23)
.
(12.23)
| Реферат | Библиотека | Ссылки | Биография | Индивидуальное задание |