Томилин Е.М., Чичикало Н.И., Ларин В.Ю. Наукові праці Донецького національного технічного університету. Серія: "Обчислювальна техніка та автоматизація". Випуск 106. - Донецьк: ДонНТУ 2006.-213с.

АНАЛИЗ ХАРАКТЕРА ПОВЕДЕНИЯ Э.Д.С. ХРОМЕЛЬ-КОПЕЛЕВОЙ ТЕРМОПАРЫ ПРИ ПОВЫШЕНИИ ТЕМПЕРАТУРЫ ЕЁ ХОЛОДНОГО КОНЦА

 

Томилин Е.М.

руководитель: д.т.н., проф. Чичикало Н.И.

 

         Аннотация. В данной статье приведен анализ  изменения термо э.д.с. различных  термопар, при повышении температуры холодного конца спая, с целью установления закона её  изменения.

Введение. Современный, высокий уровень развития науки и техники требует соответствующего уровня развития приборостроения. На данный момент промышленность использует огромное количество различных технологических процессов в которых необходимо измерять температуру. Одним из широко распространённых методов измерения данного параметра является контактный метод с применением термопар. При этом одним из основных источников погрешностей измерений является погрешность от ненулевого значения температуры холодного конца спая.

 

В соответствии с ГОСТ 30440-94 номинальная статическая передаточная характеристика, для термоэлектрического преобразователя типа ТХК, описывается полиномом следующего вида:

 

 

где Т – текущие значения температуры в градусах Цельсия.

Кроме того в данном стандарте имеются градуировочные характеристики, учитывающие изменение термо э.д.с. при изменении температуры холодного конца спая. Данные характеристики хорошо аппроксимируются полиномом четвёртой степени в пакете MathCAD 2001 Professional Edition. Здесь F0(х) – матрица аппроксимирующей функции, linfit – функция, которая выполняет аппроксимацию методом наименьших квадратов между Т – матрицей температуры и Е00 – матрицей значений

 

термо э.д.с. приведенной в ГОСТ 3044-94, h00 – матрица коэффициентов, стоящих при элементах матрицы F0(х), полученная в результате аппроксимации. U0(Т) – полином четвёртой степени, которым мы аппроксимируем значения функции термо э.д.с.:

 

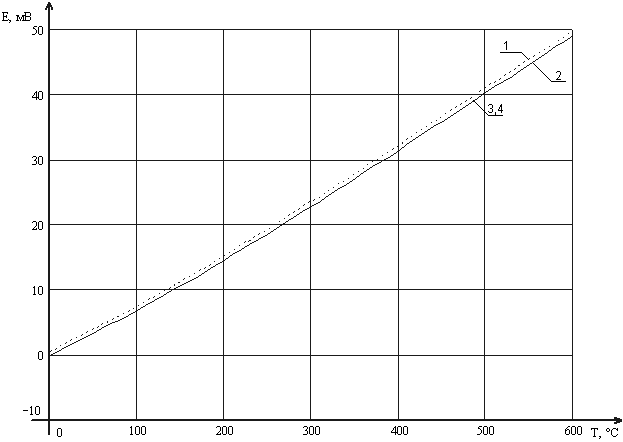
Рисунок 1 – Аппроксимация НСХ ТХК (L)

 

Здесь 2 – НСХ термопары при диапазоне измеряемых температур от 0 до 600 °С и температуре холодного конца спая равной 0 °С; 1 - … 9 °С;          3 – аппроксимирующий полином 8-й степени при температуре холодного конца спая равной 0 °С; 4 – вновь установленный по градуировочной характеристике полином 4-й степени при температуре холодного конца спая равной 0 °С.

Если объединить коэффициенты в полиномах при одинаковых степенях, для температур холодного конца спая от 0 до 9 °С то можно прийти к выводу, что данные коэффициенты изменяются случайным образом. Однако из-за малого числа наблюдений (10) невозможно оценить закон, по которому изменяются значения данных коэффициентов:

 

Таблица 1 – Коэффициенты аппроксимирующих полиномов

Температура холодного конца спая, °С	Коэффициенты при степенях аппроксимирующих полиномов 4-й степени
	1
0	-3.28922E-3	0.06357	5.54027E-5	-4.81157E-8	1.0878E-11
1	0.06014	0.06369	5.52049E-5	-4.79198E-8	1.07477E-11
2	0.1239	0.0638	5.50959E-5	-4.80087E-8	1.08822E-11
3	0.18858	0.06383	5.58156E-5	-5.05338E-8	1.31279E-11
4	0.25162	0.06402	5.48156E-5	-4.79392E-8	1.08975E-11
5	0.3235	0.06377	5.79331E-5	-5.75648E-8	1.95959E-11
6	0.37965	0.06424	5.45117E-5	-4.78445E-8	1.09182E-11
7	0.43775	0.06469	5.07501E-5	-3.57246E-8	-8.77645E-13
8	0.50802	0.06446	5.42369E-5	-4.78196E-8	1.09872E-11
9	0.57237	0.06457	5.40811E-5	-4.77522E-8	1.09702E-11

 

         Однако можно сделать предположение, что при изменении температуры холодного конца спая происходит лишь сдвиг НСХ данной термопары вверх по оси термо э.д.с. Эта зависимость хорошо аппроксимируется полиномами с первой по шестую степень включительно в пакете MathCAD 2001 Professional Edition в диапазоне 0…9 °С. Однако вне данного диапазона наблюдается сильный разброс характеристик для полиномов 5-й степени и выше:

 

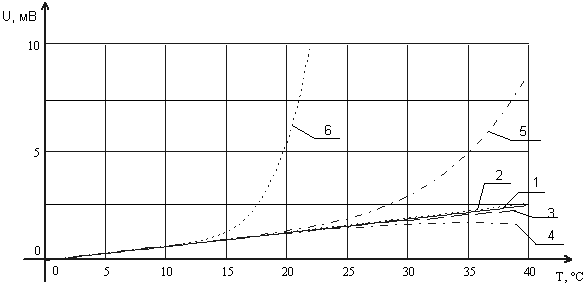
Рисунок 2 – Аппроксимация сдвига НСХ (L) по оси т.э.д.с.

 

Здесь 1 – аппроксимирующий полином 1-й степени, 2 – полином 2-й степени, 3 – полином 3-й степени и т.д.

Для аппроксимации НСХ хромель-алюмелевой термопары в          ГОСТ 3044-94 предусмотрена функция следующего вида:

 

 

Здесь Т – текущее значение температуры в градусах Цельсия, с1 – коэффициент равный 1.185976·10², 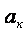- элементы матрицы:

 

 

Данная функция отличается от функции применяемой для аппроксимации НСХ хромель-копелевой термопары. В ней присутствует экспонента, которая позволяет получить максимальную точность, соответствующую первому классу, в отличие от максимальной точности соответствующей второму классу для термопары типа хромель-копель. Причём контролируемый диапазон температур, в котором мы можем получить такой высокий класс точности, для данной термопары градуировки К шире, чем для термопары градуировки L. Это свойство наряду с  относительно низкими ценами на термоэлектрические преобразователи данного типа обуславливает их широкое применение.

На рис. 3 изображена аппроксимация НСХ ТХА (К) представленной выше функцией. Здесь 1 – это НСХ ТХА (К) при температуре холодного конца спая равной 0 °С, 2 – это НСХ ТХА (К) при температуре холодного конца равной 9 °С, 3 – это аппроксимированная НСХ ТХА (К).

 

 

Таблица 2 – Классы точности различных термопар

Тип термо-электрического преобразовате-ля	Буквенное обозначение НСХ	Класс	Диапазон измерений, °С	Предел допустимых отклонений ±Δt, °С
ТХК	L	3	От –200 до –100 От –100 до 100	0.015·|t| 2.5
ТХК	L	2	От –40 до 300 От 300 до 800	2.5 0.0075·t
ТХА	К	3	От –200 до –167 От –167 до 40	0.015·|t| 2.5
ТХА	К	2	От –40 до 333 От 333 до 1200	2.5 0.0075·t
ТХА	К	1	От –40 до 375 От 375 до 1000	1.5 0.004·t

 

 

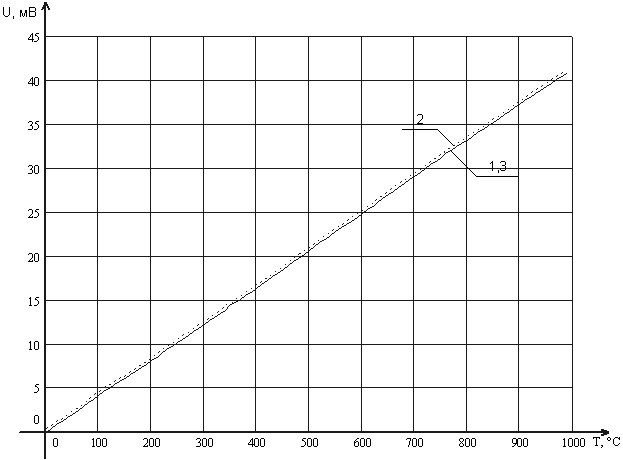
Рисунок 3 – Аппроксимация НСХ ТХА (К)

 

Основными причинами погрешностей термоэлектрических преобра­зователей температуры являются неоднородность материалов термо­электродов, изменения температуры свободных концов, шунтирующее влияние сопротивления межэлектродной изоляции, временные изме­нения свойств термоэлектродов и т.п.

Стандартом нормируется лишь погрешность градуировки. В то же время иные ее составляющие могут оказать существенное влияние на результат изменения температуры. Особенно существенными могут оказаться погрешности, вызванные временным изменением свойств термоэлектродов, обусловленным загрязнением термоэлектродов в зоне градиента температур примесями из окружающей среды или защитных оболочек, изменением процентного соотношения между компонентами термоэлектродов в результате испарения некоторых компонентов и т. д. Эти погрешности могут быть исключены лишь путем определения дей­ствительной функции преобразования и введения поправок.

Погрешность от изменения температуры свободных концов умень­шают путем ее термостабилизации или автоматическим введением по­правок, а погрешность от шунтирующего действия сопротивления меж­электродной изоляции — подбором соответствующих изоляционных материалов.

         Измерительные цепи термоэлектрических преобразователей могут быть самыми разнообразными. Простейшая измерительная цепь (рисунок 4.1, а) имеет ряд недостатков. В частности, при измерении термо-э.д.с. сравнительно низкоомным милливольтметром значительное влияние на результат измерения могут оказывать сопротивления соеди­нительных линий и материала чувствительного элемента (термопары). Действительно, показания милливольтметра связаны с термо-э.д.с. термопары зависимостью [4.1, 4.2]

 

             (4.1)

 

где Rе — сопротивление термопары; R_л = R_л1 + R_л2 — сопротивле­ние соединительных линий; R_mv — сопротивление милливольтметра.

Из последнего выражения следует, что погрешностью от влияния сопротивлений R₀ и R_л можно пренебречь лишь в том случае, когда R₀+R_л<<R_mv. Полностью устранить влияние этих сопротивлений на результат измерения можно лишь при измерении компенсационным методом.

Градуировка термопар осуществляется при температуре свобод­ных концов, равной нулю. Если в процессе измерения температура сво­бодных концов отличается от нуля, то это ведет к появлению дополни­тельных погрешностей, устранить которые можно путем термостатирования свободных концов либо схемным способом. Следует отметить, что термоэлектроды не всегда можно сделать достаточно длинными,

 

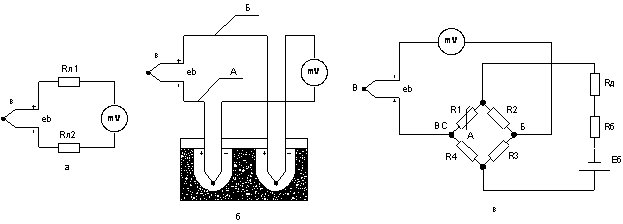
Рисунок 4.2 - Измерительные цепи термоэлектрических преобразователей.

 

чтобы можно было осуществить термостатирование свободных концов. Кроме того, для термопар из благородных металлов делать длинными термоэлектроды экономически нецелесообразно. В этих случаях ис­пользуют так называемые удлинительные термоэлектроды А и Б (рисунке 4.2, б), идущие от зажимов в головке термопары до места нахож­дения свободных концов в термостате.

Материалы удлинительных термоэлектродов должны быть термо­электрически идентичны с основной термопарой, и места их присоеди­нения к основным термоэлектродам должны иметь одинаковую темпе­ратуру. Для термопары платинородий-платина применяют удли­нительные термоэлектроды из меди и сплава ТП, для термопары хромель-алюмель - из меди и константана, а для термопары хро­мель-копель - из тех же материалов, что и основные термо­электроды.

На рисунке 4.2, в приведена схема, применение которой позволяет автоматически осуществлять коррекцию температуры свободных кон­цов. В этой схеме между термопарой и вторичным прибором включен неуравновешенный мост, состоящий из манганиновых резисторов R2, R3, R4 и медного резистора R1, который находится в таких же температурных условиях, как и свободные концы термопары. Пара­метры моста подбирают таким образом, чтобы при значении температу­ры свободных концов, равном нулю, мост находился в равновесии, а при отклонении температуры свободных концов от нуля между вер­шинами А — Б моста возникала разность напряжений U_К, равная по значению изменению термо-э.д.с. термопары, вызванному изме­нением температуры свободных концов. Значение ΔU_к может быть опре­делено из выражения

 

   (4.2)

 

где Eб и R_б — э.д.с. и внутреннее сопротивление источника пита­ния моста; R_l0 — значение сопротивления R1 при температуре 0°С; α — температурный коэффициент сопротивления резистора R1; R_д — добавочное сопротивление; θ_с — температура свободных концов (и ре­зистора R1).

 

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

 

1. Скрипник Ю.А. – Повышение точности измерительных устройств. – Изд-во. «Техніка», Киев, 1986

2.     Головко Д.Б., Скрипник Ю.О., Хімічева Г.І. Структурно-алгоритмічні методи підвищення точності вимірювання температури. – К.: ФАДА, ЛТД, 1999. – 206 с.

3.     Ким Нарзан. Исследование усовершенствованного градиентометрического метода измерения температуры // Наукові праці Донецького державного технічного університету. Серія: Обчислювальна техніка та автоматизація. – Вип.3. – Донецьк.

4.     Орнатский П.П. Теоретические основы информационно-измерительной техники. – 1983. – 304 с.

5.     Полищук Е.С. “Измерительные преобразователи” Киев, Вища Школа. Головное издательство 1981г. - 296с.