Навигация

   




 

Анализ вибрации вращающихся механизмов при изменении скорости вращения

Михаил Манжелий
http://www.acs-inc.ru/technology/compar00.shtml

Сравнение порядкового анализа и гармонического анализа

В классическом гармоническом анализе хорошо известно, что основная частота не изменяется во времени. Вмете с тем фазы и амплитуды отдельных спектральных составляющих изменяются во времени, а центральные частоты каждой гармрнической составляющей постоянны.Другими словами, гармонический анализ подходит только тогда, когда скорость вращения деталей машины постоянна.

При постоянной частоте вращения номер гармоники (order) может быть хорошо идентефицирован одновременно с общепринятым спектром мощности и грфиком зависимости частоты от времени.

Во многих случаях существенный интерес представляет анализ вибраций при наборе скорости вращения или замедлении. Одной из наиболее важных задач решаемых при помощи Order Analysis является извлечение информации о порядках гармоник которые могут содержаться в спектре мощности во время изменения скорости. Т.е. в случае когда центральные частоты гармоник меняются во времени.

Applications of Order Analysis
Применения Order Analysis

1. Сопоставление свойств сигналов вибрации и шума с характеристиками машин.
2. Идентификация характеристик которые изменяются во времени, что важно при проектировании или поике неисправностей.

Signal Processing
Обработка сигналов

Метод Re-Sampling

Re-Sampling один из наиболее широко применяющихся методов при Order Analysis (анализе порядка гармоник). На figure 3-1 показан этот метод.


Этот метод предполагает преобразование измерений проводящихся через одинаковые промежутки времени в измерения проводящиеся через одинаковые приращения угла. В дальнейшем сигнал может быть подвергнут преобразованию Фурье.

Получить зависимость амплитуды спектральных компонент от оборотов можно двумя способами.

Первый способ - использовать сигнал от датчика оборотов как старт-стоп для аналогово цифрового преобразования сигнала от датчика вибрации.

Второй способ - одновременно оцифровывать сигналы от датчика оборотов и датчика вибрации с одинаковой скоростью. Затем интерполировать и апроксимировать сигнал от датчика ускорений, беря за узловые точки те которые соответствуют одинаковому приращению угла. Для первого способа нужно дополнительное устройство, для второго нет. После того как измерения при одинаковом приращении угла выполнены можно делать преобразование Фурье, при этом время пересчитывается в приращение угла , а частота в порядок гармоники.

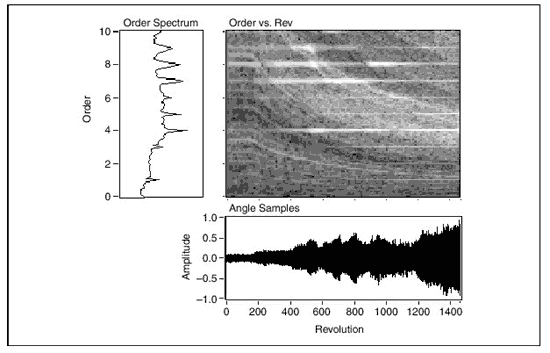
На figure 3-2 показана спектрограмма, полученная при взятии отсчетов через одинаковые приращения угла. Нижний график (angle-samples) является сигналом полученным через одинаковые значения приращения угла. (angle - угол, samples-отсчеты). График слева вверху (Order Spectrum) показывает спектр порядка гармоник, вычисленный как преобразование Фурье сигнала, взятого через одинаковые приращения угла. На графике Order Spectrum значимые пики появляются в порядке возрастания номера гармоники. Справа вверху график Order vs. Rev (Порядок гармоники от оборотов) как результат вычисления STFT (short-time Fourier transform) короткого преобразования Фурье, где вместо оси частоты показана ось порядка гармоники. (Пересчитать порядок гармоники в частоту очень просто. Для этого нужно разделить обороты детали в минуту на 60 и результат умножить на порядок гармоники) Каждая горизонтальная светлая линия показывает величину сигнала во всем диапазоне оборотов. После этих преобразований восстановление исходного сигнала может вызвать затруднения.



Adaptive Filter
Адаптивная фильтрация

Несмотря на то, что частоты гармоник изменяются в зависимости от скорости вращения во времени, можно предположить ,что скорость вращения и частоты могут быть постоянными за короткий интервал времени.

В методе адаптивной фильтрации используются полосовые фильтры, при помощи которых выделяютя интересующие гармоники. Фильтры Калмана могут быть хорошим примером решения этой задачи. Фильтр Калмана (Vold-Kalman Order Tracking Fiter) может извлекать два номера гармоник, которые очень хорошо различаются.

Gabor Transform
Преобразование Габора

Преобразование Габора одно из обратимых (invertible) частотно временных преобразований. Это значит, что любой сигнал зависящий от времени может быть восстановлен путем применения инверсного преобразования Габора. Результатом преобразования являются коэффициенты Габора а инверсное преобразование известно как расширение (expansion) Габора.

Преобразование Габора может быть вычислено при помощи преобразования STFT или Фурье преобразования массива на который наложено окно, например Ханнинга. Однако, для обеспечения реконструкции сигнала, вы должны очень аккуратно работать с окном, сдвигом окна, фронтом сигнала. Следующие методы используют для обеспечения реконструкции сигнала:

1. Отношение между длиной анализируемого окна и сдвигом должно быть больше или эквивалентно единице. Это отношение определяет временное перекрытие. По умолчанию в наборе инструментов Order Analysis Toolset это отношение равно четырем. Например, если длина окна равна 2048 то величина сдвига равна 512.
2. Анализируемое окно нужно перемещать так, чтобы не было потери информации, особенно в начале и в конце сигнала.

Overview of the Order Analysis Toolset Algorithm
Введение в порядковый анализ

Базирующийся на преоразовании Габора набор инструментов для порядкового анализа (Order Analisis Toolset) для LaBVIEW представляет новый метод, применяя который можно полностью решить следующие задачи:

1. Анализировать компоненты сигнала вибрации или шума
2. Реконструировать нужные компоненты во временной области

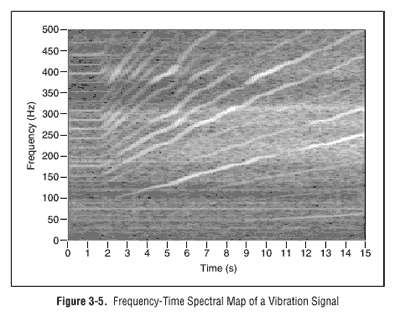
Преобразование Габора может давать распеделение мощности исходного сигнала как функцию одновременно времени и частоты. На figure 3-5 показана частотно-временная карта, полученная после вычисления преобразования Габора для простого сигнала вибрации вращающегося механизма. Горизонтальная ось определяет время, а вертикальная ось определяет частоту. Величина коэффициентов определяет цвет, для черно белой шкалы белый цвет соответствует максимальной величине, черный минимальной.

Так как скорость вращения изменяется не сильно в каждый промежуток времени, спектр каждой составляющей хорошо различим. Вместае с изменением скорости вращения центральная частота каждой составляющей также изменяется во времени. Таким образом, хорошо видно, что светлые линии , соответствующие каждой составляющей искривляются на частотно временной карте, как показано на figure 3-5. Светлые кривые имеют большую величину чем более темные в их окрестности. Эти светлые кривые показывют порядок компонент (гармоник) и соответствуют каждая своему порядковому номеру.


Из частотно-временной карты мы можем выделить порядки гармоник, или другие части сигнала, которые ас интересуют. Далее мы можем восстановить эти части сигнала в координатах амплитуда-время, используя преобразование Габора.

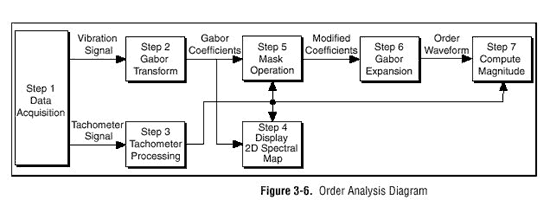
На figure 3-6 показан весь процесс работы порядкового анализа Order Analysis.

Этот процесс состоит из следующих шагов:

1. Измерение сигналов тахометра и синхронно сигналов вибродатчика с одинаковой скоростью оцифровки сигнала. [Step 1 Data Acquisition]
   Vibration Signal - сигнал датчика вибрации
   Tachometer Cignal - сигнал датчика оборотов(тахометр)
2. Выполнение преобразования Габора первоначальное определение коэффициентов Габора. [Step 2 Gabor Transform]
3. Вычисление скорости вращения по сигналу тахометра [Step 3 Tachometer Processing]
4. Создание двумерной спектральной карты из первоначально определенных коэффициентов Габора для просмотра полной картины в координатах частота-время, частота- обороты в минуту, порядок(гармоники)- обороты в минуту, обороты в минуту - порядок. [Step 4 Display 2D Spectral Map]
5. Повторное вычисление коэффициентов Габора, с учетом интересующего диапазона скорости и гармоники, путем выполнения операции маскирования. [Step 5 Mask Operation]
6. Генерация сигнала во временной области путем выполнения преобразования Габора над вычисленными коэффициентами. [Step 6 Gabor Expansion]
7. Вычисление амплитуды сигнала как функции оборотов.