Навигация

   




 

ОСНОВЫ ИЗМЕРЕНИЯ ВИБРАЦИИ

Источник:http://www.vibration.ru/osn_vibracii.shtml

Что такое вибрация?

    Вибрация - это механические колебания тела.
    Самый простой вид вибрации - это колебание или повторяющееся движение объекта около положения равновесия. Этот тип вибрации называется общей вибрацией, потому что тело перемещается как единое целое и все его части имеют одинаковую по величине и направлению скорость.Положением равновесия называют такое положение, в котором тело находится в состоянии покоя или положение которое оно займет, если сумма действующих на него сил равна нулю.
    Колебательное движение твердого тела может быть полностью описано в виде комбинации шести простейших типов движения: поступательного в трех взаимно перпендикулярных направлениях (х, у, z в декартовых координатах) и вращательного относительно трех взаимно перпендикулярных осей (Ох, Оу, Оz). Любое сложное перемещение тела можно разложить на эти шесть составляющих. Поэтому о таких телах говорят, что они имеют шесть степеней свободы.
    Например, корабль может перемещаться в направлении оси "корма-нос" (прямо по курсу), подниматься и опускаться вверх-вниз, двигаться в направления оси правый борт-левый- борт, а также вращаться относительно вертикальной оси и испытывать бортовую и килевую качку.
    Представим себе некий объект, перемещения которого ограничены одним направлением, например, маятник настенных часов. Такая система называется системой с одной степенью свободы, т.к. положение маятника в любой момент времени может быть определено одним параметром- углом в точке закрепления. Другим примером системы с одной степенью свободы является лифт, который может перемещаться только вверх и вниз вдоль ствола шахты.
    Вибрация тела всегда вызывается какими-то силами возбуждения. Эти силы могут быть приложены к объекту извне или возникать внутри него самого. Далее мы увидим, что вибрация конкретного объекта полностью определяется силой возбуждения, ее направлением и частотой. Именно по этой причине вибрационный анализ позволяет выявить силы возбуждения при работе машины. Эти силы зависят от состояния машины, и знание их характеристик и законов взаимодействия позволяет диагностировать дефекты последней.

Простейшее гармоническое колебание

    Самыми простыми из существующих в природе колебательных движений являются упругие прямолинейные колебания тела на пружине (рис.1).

   
    Рис. 1. Пример простейшего колебания.

    Такая механическая система обладает одной степенью свободы. Если отвести тело на некоторое расстояние от положения равновесия и отпустить, то пружина вернет его в точку равновесия. Однако тело приобретет при этом определенную кинетическую энергию, проскочит точку равновесия и деформирует пружину в противоположном направлении. После этого скорость тела начнет уменьшаться, пока оно не остановится в другой крайней позиции, откуда сжатая или растянутая пружина опять начнет возвращать тело назад в положение равновесия. Такой процесс будет повторяться вновь и вновь, при этом происходит непрерывное перетекание энергии от тела (кинетическая энергия) к пружине (потенциальная энергия) и обратно.
    На рис.1 представлен также график зависимости перемещения тела от времени. Если бы в системе отсутствовало трение, то эти колебания продолжались бы непрерывно и бесконечно долго с постоянными амплитудой и частотой. В реальных механических системах такие идеальные гармонические движения не встречаются. Любая реальная система обладает трением, которое приводит к постепенному затуханию амплитуды и превращает энергию колебаний в тепло. Простейшее гармоническое перемещение описывается следующими параметрами:
    Т - период колебаний.
    F - частота колебаний, = 1/Т.
    Период - это интервал времени, который необходим для завершения одного цикла колебания, то есть это время между двумя последовательными моментами пересечения нулевой точки в одном направлении. В зависимости от быстроты колебаний, период измеряют в секундах или миллисекундах.
    Частота колебаний - величина обратная периоду, определяет количество циклов колебания за период, она измеряется в герцах (1Гц= 1/секунду). Когда рассматриваются вращающиеся машины, то частота основного колебания соответствует частоте вращения, которая измеряется в об/мин (1/мин) и определяется как:

= F х 60,

    где F- частота в Гц,
    т.к. в минуте 60 секунд.

Уравнения колебаний

    Если по вертикальной оси графика отложить положение (смещение) объекта, испытывающего простые гармонические колебания, а по горизонтальной шкале- время (см. рис.1), то результатом будет синусоида, описываемая уравнением:
    d=D sin(t),
где d-мгновенное смещение;
    D-максимальное смещение;
    = 2F - угловая (циклическая) частота, =3,14.

Это та самая синусоидальная кривая, которая всем хорошо известна из тригонометрии. Ее можно считать простейшей и основной временной реализацией вибрации. В математике функция синуса описывает зависимость отношения катета к гипотенузе от величины противолежащего угла. Синусоидальная кривая при таком подходе является просто графиком синуса в зависимости от величины угла. В теории вибраций синусоидальная волна также является функцией времени, однако один цикл колебания иногда рассматривают также как изменение фазы на 360 градусов. Об этом мы еще поговорим подробнее при рассмотрении понятия фазы.
    Упомянутая выше скорость движения определяет быстроту изменения положения тела. Скорость (или быстрота) изменения некоторой величины относительно времени, как известно из математики, определяется производной по времени:

=dd/dt= Dcos(t),
    где n - мгновенная скорость.
    Из этой формулы видно, что скорость при гармоническом колебании также ведет себя по синусоидальному закону, однако, вследствие дифференцирования и превращения синуса в косинус, скорость сдвинута по фазе на 90 (то есть на четверть цикла) относительно смещения.
    Ускорение - это скорость изменения скорости:

a=d /dt= -² Dsin(t),
    где а - мгновенное ускорение.
    Следует отметить, что ускорение сдвинуто по фазе еще на 90 градусов, на что указывает отрицательный синус (то есть на 180 градусов относительно смещения).

Из приведенных уравнений видно, что скорость пропорциональна смещению, умноженному на частоту, а ускорение - смещению, умноженному на квадрат частоты.
    Это означает, что большие смещения на высоких частотах должны сопровождаться очень большими скоростями и чрезвычайно большими ускорениями. Представьте, например, вибрирующий объект, который испытывает смещение 1 мм с частотой 100 Гц. Максимальная скорость такого колебания будет равна смещению, умноженному на частоту:
    =1 х 100 =100 мм с
    Ускорение равно смещению, умноженному на квадрат частоты, или
    а = 1 х (100)² = 10000 мм с² = 10 м с²
    Ускорение свободного падения g равно 9,81м/ с2. Поэтому в единицах g полученное выше ускорение приблизительно равно
    10/9,811 g
    Теперь посмотрим, что произойдет, если мы увеличим частоту до 1000 Гц
    =1 x 1000 = 1000 мм с =1 м/с,
    а = 1 x (1000)² = 1000000 мм /с² = 1000 м/ с² = 100 g
    Таким образом, мы видим, что высокие частоты не могут сопровождаться большими смещениями, поскольку возникающие в этом случае огромные ускорения вызовут разрушение системы.

Динамика механических систем

    Небольшое компактное тело, например кусочек мрамора, можно представить как простую материальную точку. Если приложить к ней внешнюю силу, она придет в движение, которое определяется законами Ньютона. В упрощенном виде, законы Ньютона гласят, что покоящееся тело будет оставаться в покое, если на него не действует внешняя сила. Если же к материальной точке приложена внешняя сила, то она придет в движение с ускорением, пропорциональным этой силе.
    Большинство механических систем является более сложными, чем простая материальная точка, и они совсем не обязательно будут перемещаться под воздействием силы как единое целое. Роторные машины не являются абсолютно твердыми и отдельные их узлы имеют различные жесткости. Как мы увидим далее, их реакция на внешнее воздействие зависит от природы самого воздействия и от динамических характеристик механической конструкции, причем эту реакцию очень тяжело предсказать. Проблемы моделирования и предсказания реакции конструкций на известное внешнее воздействие решаются с помощью метода конечных элемнтов (МКЭ) и модального анализа. Здесь мы не будем подробно останавливаться на них, так как они достаточно сложны, однако для понимания сущности вибрационного анализа машин полезно рассмотреть, как взаимодействуют между собой силы и конструкции.

Измерения амплитуды вибрации

    Для описания и измерения механических вибраций используются следующие понятия:
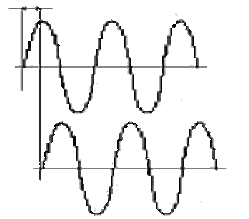
    Максимальная Амплитуда (Пик) - это максимальное отклонение от нулевой точки, или от положения равновесия.
    Размах (Пик-Пик) - это разница между положительным и отрицательным пиками. Для синусоидального колебания размах в точности равен удвоенной пиковой амплитуде, так как временная реализация в этом случае симметрична. Однако, как мы скоро увидим, в общем случае это неверно.
   

    Среднеквадратическое значение амплитуды (СКЗ) равно квадратному корню из среднего квадрата амплитуды колебания. Для синусоидальной волны СКЗ в 1,41 раза меньше пикового значение, однако такое соотношение справедливо только для данного случая.
    СКЗ является важной характеристикой амплитуды вибрации. Для ее расчета необходимо возвести в квадрат мгновенные значения амплитуды колебаний и усреднить получившиеся величины по времени. Для получения правильного значения, интервал усреднения должен быть не меньше одного периода колебания. После этого извлекается квадратный корень и получается СКЗ.

   

    СКЗ должно применяться во всех расчетах, относящихся к мощности и энергии колебания. Например, сеть переменного тока 117В (речь идет о северо-американском стандарте). 117 В - это среднеквадратичное значение напряжения, которое применяется для расчета мощности (Вт), потребляемой включенными в сеть приборами. Напомним еще раз, что для синусоидального сигнала (и только для него) среднеквадратичная амплитуда равна 0,707 х пик.

Понятие фазы

    Фаза есть мера относительного сдвига во времени двух синусоидальных колебаний. Хотя по своей природе фаза является временной разностью, ее почти всегда измеряют в угловых единицах (градусах или радианах), которые представляют собой доли цикла колебания и, следовательно, не зависят от точного значения его периода.

 

Задержка 1/4 периода = сдвигу по фазе на 90 градусов.................