 |
Библиотека
Инженер. Студентський науково-технічний журнал. – Донецьк: ДонНТУ, 2005 № 6 – С. 87 – 90.
СРАВНЕНИЕ УСТОЙЧИВОСТИ СТЕРЖНЯ И СВЕРЛА ПОД ДЕЙСТВИЕМ ОСЕВОЙ
СИЛЫ И КРУТЯЩЕГО МОМЕНТА
Федосов Н.Н., Коваленко В.И.
(каф.ТМ, ДонНТУ, г. Донецк, Украина)
Одной из важнейших проблем, возникающих в процессе сверления,
является устойчивость сверл, нагруженных силами резания. На первоначальном этапе
для расчета устойчивости сверл принимаем вместо поперечного сечения обычного
спирального сверла, которое имеет сложную форму, сечение стержня, которое имеет
простую форму круглого сечения.
Произведем расчет устойчивости стержня и сверла, находящихся под действием
осевой сжимающей силы (рис. 1).

Из формулы для вычисления критической осевой сжимающей силы для стержня с
шарнирно опертыми концами [1, с.626], если критическую силу заменить на
Pо, найдем критическую длину стержня lРо, при
увеличении которой его прямолинейная форма теряет устойчивость:

где Bx и By - наибольшая и наименьшая жесткость
сечения стержня [2, с.346]:

где E - модуль продольной упругости первого рода; Imax и
Imin - наибольшый и наименьшый момент инерции сечения стержня.
Для стержня, имеющего симметричное круглое сечение [2, с.346]:

Для сверла [1, с.626]:
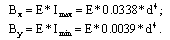
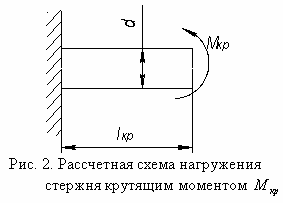
Произведем расчет устойчивости стержня и сверла, находящихся под действием
крутящего момента Мкр (рис. 2).
Из формулы для вычисления критического крутящего момента для стержня с
шарнирно опертыми концами [1, с.633], если критический момент заменить
Мкр, найдем критическую длину стержня lМкр, при
увеличении которой его прямолинейная форма теряет устойчивость:
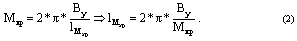
Для пояснения полученных зависимостей выполним числовой пример. Произведем
расчет устойчивости стержня и сверла, находящихся под действием осевой сжимающей
силы и крутящего момента. Для расчета примем следующие исходные условия:
номинальный диаметр d=5мм; материал стержня и сверла – быстрорежущая сталь Р6М5;
модуль упругости для этой стали Е=2*105 Н/мм. При обработке сверлом
d=5мм, изготовленным из быстрорежущей стали Р6М5, рекомендуемые по справочнику
[3] режимы резания составляют: s=0,047мм/об, n=2250 об/мин; при этом возникает
осевая сжимающая сила Ро=455.66Н и крутящий момент
Мкр=0.64*103Нмм. Указанные значения Ро и
Мкр примем в качестве расчетных при определении критической длины как
стержня, так и сверла.
Выполним расчет устойчивости стержня и сверла, находящихся под действием
осевой сжимающей силы Ро=455.66Н для случая сверления отверстия
диаметром d=5мм.
Жесткость сечения стержня:

Используя выражение (1) и подставляя в него численные значения, найдем
критическую длину стержня:

Жесткость сечения сверла:

Используя выражение (1) и подставляя в него численные значения, найдем
критическую длину сверла:
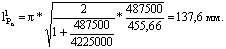
Произведем расчет устойчивости стержня и сверла, находящихся под действием
крутящего момента Мкр=0.64*103Нмм. Используя выражение (2)
и подставляя в него численные значения, найдем критическую длину стержня:
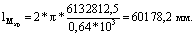
Используя выражение (2) и подставляя в него численные значения, найдем
критическую длину сверла:

Используя полученные выше зависимости, произведены расчеты для наиболее
широко используемого диапазона диаметров сверл 5 - 50 мм. В результате
выполненных расчетов получены криволинейные зависимости, представленные на
диаграмме (рис. 3).
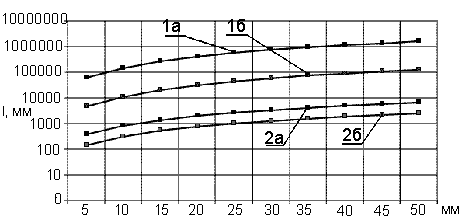 |
Рис.3 Движение критической длины стержня сверла в зависимости от их размера:
1- критическая длина при кручении 1а-стержня, 1б -сверла
2 -критическая длина при сжатии 2а-стержня, 2б -сверла |
Для большей наглядности полученных результатов для сверл (при кручении и
сжатии) определено критическое отношение длины сверла к его диаметру l/d;
результаты сведены в табл.1.
Таблица 1. Отношение длины сверла к диаметру при кручении и
сжатии сверл
| Диаметр сверла d, мм |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
| l/d при кручении |
956,7 |
1100,8 |
1365,2 |
1575,7 |
1784,5 |
1960,8 |
2113,3 |
2247,1 |
2396,7 |
2533,1 |
| l/d при сжатии |
27,5 |
30,5 |
34,4 |
37,3 |
39,9 |
42,1 |
44,9 |
45,5 |
47,1 |
48,6 |
По результатам, приведенным в табл. 1, построены графики
изменения отношений l/d при кручении и сжатии сверла (рис. 4); (числовые данные,
соответствующие ломаной линии 2, увеличены в 50 раз для сопоставления обеих
линий, приведенных на графике).
 |
| Рис.4 Зависимость V от d 1- при кручении, 2 - при сжатии |
По полученным данным можно сделать следующие выводы
1. Устойчивость стержня выше, чем сверла, вследствие его большего по площади
поперечного сечения.
2. На потерю устойчивости стержня и сверла осевая сила оказывает большее
влияние, чем крутящий момент.
3. С ростом расчетного диаметра d критическое отношение l/d увеличивается.
4. Увеличение отношения l/d является более крутым при сжатии и более пологим
– при кручении.
Список литературы:
1. Пономарев С.Д. Основы современных методов
расчета на прочность в машиностроении./М: Машгиз, 1952. – 864с.
2. Сопротивление
материалов/Под ред. Писаренко Г.С. – 5-е изд. – К: Вища шк. Головное изд-во,
1986. – 775с.
3. Справочник технолога-машиностроителя. В 2-х т. Т. 2. Под ред.
А.М. Дальского. - М.: Машиностроение -1, 2001. - 944 с.
|
 |





