Особенности динамического моделирования формообразующих
движений при сверлении глубоких отверстий малого диаметра.
Назаренко Д.В. Панов Е.Ю. Потапенко П.Н.
При изучении процессов сверления наиболее важным этапом
является построение динамических моделей. В данной работе рассматривается анализ
разработанных алгоритмов математического моделирования, показаны их преимущества
и недостатки. Приведены результаты моделирования и сделаны выводы об
устойчивости системы.
Сверление глубоких отверстий малого диаметра выполняется на
силовых сверлильных станках, с управляемыми приводами подачи и вращения шпинделя
[1,2]. Схема силовой сверлильной головки приведена на рис. 1.

Рис. 1. Схема силовой сверлильной головки.
Использование управляемых двигателей необходимо для организации
циклов обработки с периодическим выводом инструмента из зоны резания по
необходимым траекториям формообразующих движений. Вектор управления подбираются
таким образом, чтобы обеспечить обработку без поломок режущего инструмента при
удовлетворении заданных показателей производительности, качества и прежде всего
точности оси обрабатываемого отверстия.
Известные схемы обработки базируются на управлении скоростью
подачи режущего инструмента при неизменной частоте вращения шпинделя. Однако
можно существенно увеличить эффективность процесса, если обеспечить векторное
управление путем одновременного варьирования скорости подачи и частоты вращения
шпинделя. Это связано с тем, что скорость резания существенно влияет на
особенности динамики процесса и особенно на интенсивность нарастания крутящего
момента сверла, который непосредственно связан с вероятностью его поломки.
Векторное управление отличается от скалярного тем, что относительно независимые
приводы подачи и частоты вращения шпинделя становятся связанными через процесс
резания. Если не учитывать упругие деформации механической части системы и
считать механическую часть привода абсолютно жесткой, то уравнение движения
системы с учетом векторного управления можно представить в матричном виде:
|

|
(1) |
где 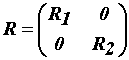 ,
,
 ,
,
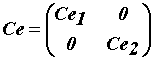 ,
,
 ,
,
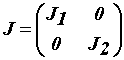 - матрицы сопротивлений, индуктивностей, постоянных двигателей и моментов
инерции,
- матрицы сопротивлений, индуктивностей, постоянных двигателей и моментов
инерции, 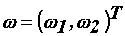 ,
,
 ,
,
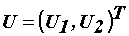 – вектора частот вращения, токов и напряжений якорей двигателей подачи и
вращения сверла;
– вектора частот вращения, токов и напряжений якорей двигателей подачи и
вращения сверла; 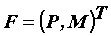 – осевая сила и крутящий момент - вектор составляющих силы, действующей на
инструмент.
– осевая сила и крутящий момент - вектор составляющих силы, действующей на
инструмент.
Для раскрытия динамической модели необходимо выяснить
зависимость момента сопротивления от траектории движения, то есть от скорости
подачи и частоты вращения двигателя.
|
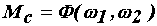
|
(2) |
В общем случае сила, действующая на инструмент в зоне резания,
пропорциональна площади срезаемого слоя. В случае сверления, сила резания может
быть выражена следующим соотношением:
|
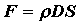
|
(3) |
где D – диаметр сверла, S – путь,
пройденный инструментом за оборот в течении времени Т=1/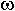 ,
то есть величина подачи на оборот;
,
то есть величина подачи на оборот; 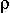 - коэффициент пропорциональности.
- коэффициент пропорциональности.
Величина S может быть представлена в следующем
виде:
|
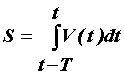
|
(4) |
Возможны два подхода представления реакции со стороны
обработки. Первый основан на разложении в ряд Тейлора:
|
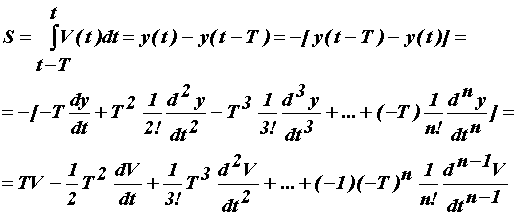
|
(5) |
Второй основан на динамическом моделировании, в котором в
текущем времени вычисляется величина оборотного запаздывания в зависимости от
текущих значений частоты вращения шпинделя. Для динамического моделирования
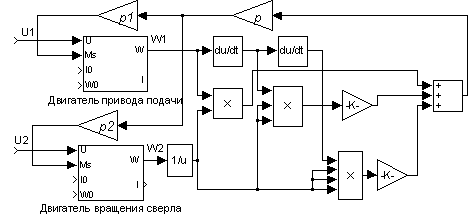
использовалась оболочка Simulink пакета MatLab 5.2. На рис. 2
приведена блок-схема, организующая оба алгоритма.
а)

б)
Рис. 2. Блок-схемы процесса сверления. (а - Алгоритм 1 б -
Алгоритм 2)
Практика работы с предложенными моделями показала, что для
увеличения точности машинного моделирования с использованием первого алгоритма
необходимо использовать полиномы Тейлора достаточно высокой степени. Однако для
обеспечения заданной точности моделирования на основе этого разложения
приходиться прибегать к операции численного дифференцирования высокого порядка,
что приводит к накоплению ошибок вычисления. (рис. 3б, 3в)

а)
|
|
|
|
б) |
в) |
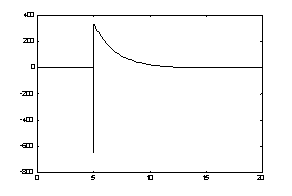
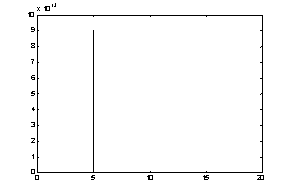
Рис. 3. Реакции скорости на единичные воздействия со стороны
управления (а – сравнительные характеристики скоростей двух методов (1-скорость
двигателя вращения сверла по методу 1, 2-скорость двигателя вращения сверла по
методу 2, 3-скорость двигателя подачи по методу 1, 4-скорость двигателя подачи
по методу 2); б – производная скорости подачи в методе 1; в – вторая производная
скорости подачи)
На рис. 3 приведены результаты вычислений реакции скорости на
единичные воздействия со стороны управления. Указанные обстоятельства привели к
необходимости использования модели 2.
Остановимся коротко на результатах динамического моделирования.
Анализ уравнений показывает, что на динамику существенно оказывает влияние
коэффициент 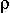 .
.
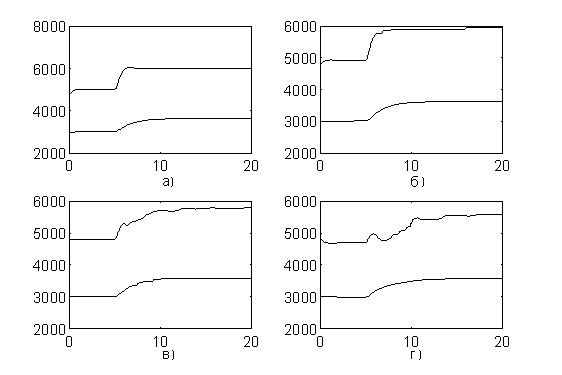
Рис. 4. Характер изменения переходных процессов (а – при 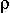 =0;
б – при
=0;
б – при 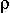 =0.1;
в – при
=0.1;
в – при 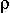 =0.3;
г - при
=0.3;
г - при 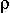 =0.5)
=0.5)
На рис. 4 приведены примеры изменения переходных процессов по
мере увеличения 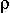 .
Осциллограммы наглядно показывают что с увеличением
.
Осциллограммы наглядно показывают что с увеличением 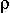 в системе возникают дополнительные колебания, генерируемые взаимосвязанными
двигателями, т.е. с увеличением
в системе возникают дополнительные колебания, генерируемые взаимосвязанными
двигателями, т.е. с увеличением 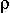 система теряет устойчивость. Механизм потери устойчивости объясняется
взаимосвязью скорости вращения инструмента, подачи и площади срезаемого слоя,
что в совокупности определяет силы в системе. При увеличении частоты вращения
инструмента площадь срезаемого слоя уменьшается и, как следствие уменьшается
сила влияющая на скорость шпинделя. Тем самым формируется прямая обратная связь,
способствующая потере устойчивости.
система теряет устойчивость. Механизм потери устойчивости объясняется
взаимосвязью скорости вращения инструмента, подачи и площади срезаемого слоя,
что в совокупности определяет силы в системе. При увеличении частоты вращения
инструмента площадь срезаемого слоя уменьшается и, как следствие уменьшается
сила влияющая на скорость шпинделя. Тем самым формируется прямая обратная связь,
способствующая потере устойчивости.
Список литературы
1. Заковоротный В.Л., Перлин О.С., Чубукин А.В. Оптимальное
управление процессом глубокого сверления. Сб. "Труды III областной конференции
молодых ученых", Ростов-на-Дону, 1973. с. 137-139.
2. Назаренко Д.В. Оптимизация процесса сверления глубоких
отверстий малого диаметра: дис. канд. техн. наук: 05.03.01 / ДГТУ. - Ростов
н/Д, 1998.- 236с.: ил.





