БИБЛИОТЕКА

ДЛИНА ДУГИ КОНТАКТА ЕДИНИЧНОГО ЗЕРНА С ЗАГОТОВКОЙ
ПРИ ПЛОСКОМ ШЛИФОВАНИИ С ОСЕВЫМИ КОЛЕБАНИЯМИ КРУГА
Матюха П.Г., Габитов В.В., Полтавец В.В.
(ДонНТУ, г. Донецк, Украина)
ИНЖЕНЕР: студенческий научно-технический журнал / Донецк: ДонНТУ, 2007
При шлифовании производительность и качество обработки зависят от условий контактирования зерна с
обрабатываемой поверхностью, определяемые формой единичных срезов и его параметров – толщиной среза,
длиной дуги контакта с заготовкой, а также количеством зерен, участвующих в процессе шлифования.
Изменить форму единичных срезов можно при помощи сообщения шлифовальному кругу колебательного движения
в направлении, перпендикулярном или параллельном оси круга. В первом случае, контактирование алмазных зерен
осуществляется в условиях переменной глубины резания. В итоге, при перемещении рабочей поверхности круга
(РПК) в направлении обрабатываемой поверхности, увеличиваются параметры единичных срезов и их количество.
При перемещении РПК от обрабатываемой поверхности, наоборот, уменьшаются как параметры среза,
так и количество одновременно работающих зерен. В результате радиальные колебания являются вредными,
их необходимо устранять, снижая до минимума их влияние на параметры шероховатости [1].
Процесс шлифования с колебаниями исследован, в основном, экспериментально. При этом установлено
повышение производительности и качества обработки как при наложении осевых колебаний на круг
[2], так
и создания эксцентрично расположенного относительно оси круга алмазоносного слоя, в результате чего при
обработке возникает осциллирующее движение РПК.
При выводе уравнения траектории движения абразивного зерна шлифовального круга, относительно
детали, при плоском шлифовании с осевыми колебаниями круга воспользуемся общим матричным уравнением,
описывающем движение детали и шлифовального круга [3].
Пусть репер 1 (система координат X1Y1Z1) связан со шлифовальным кругом,
вращается вокруг оси Z1 с
угловой скоростью и поступательно перемещается в плоскости X2О2Y2
относительно репера 2
(система координат X2Y2Z2), связанного с обрабатываемой поверхностью (рис.4).

Рисунок 4 -Положение репера 1 относительно репера 2 при плоском встречном шлифовании:
а - в начальный момент времени;
б – после поворота на некоторый угол и поступательного перемещения вдоль оси О2Z2 на
величину Sz и на величину Sx
за счет колебательного движения вдоль оси O1X1.
Уравнение движения единичного зерна шлифовального круга при плоском шлифовании в общем виде опишется равенством:

Перемещение детали Sz за время поворота круга на величину  для встречного шлифования:
для встречного шлифования: 
для попутного шлифования:
где Vд - скорость детали, м/мин;
Vк - скорость шлифовального круга, м/с;
f - частота колебаний круга вдоль его оси, Гц;
Aк - амплитуда колебаний круга, мм.
Подставив в формулу (1) соответствующие значения величин, получим матричное уравнение вида:
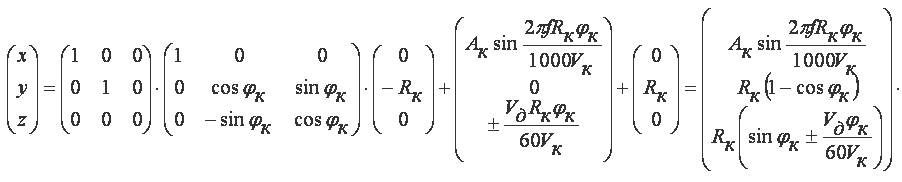
Таким образом, траектория движения абразивного зерна шлифовального круга при плоском шлифовании
представляет собой трохоиду, у которой центр образующей окружности движется по синусоидальному
гармоническому закону. Уравнение траектории движения зерна окончательно имеет вид:

Верхние знаки относятся к случаю попутного шлифования, нижние – встречного.
С использованием полученных уравнений (2) выведем формулу для определения длины дуги контакта
единичного зерна шлифовального круга с обрабатываемой деталью.
Длина дуги контакта представляет собой определенный интеграл вида:

Пределы интегрирования соответствуют моменту входа и выхода зерна из детали. После подстановки
соответствующих значений производных и необходимых преобразований интеграл (3) примет вид:
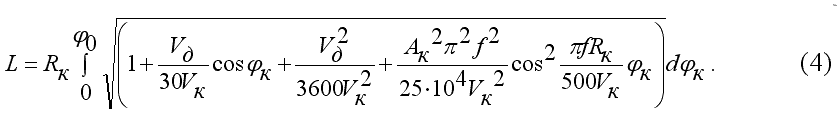
Решая интеграл (4), получим формулу для определения длины дуги контакта с использованием точной
траектории движения зерна. При этом метод решения интеграла (путем разложения подинтегрального
выражения в биноминальный ряд и использования первых трех его членов) обеспечит точность
вычислений до 0,5%:
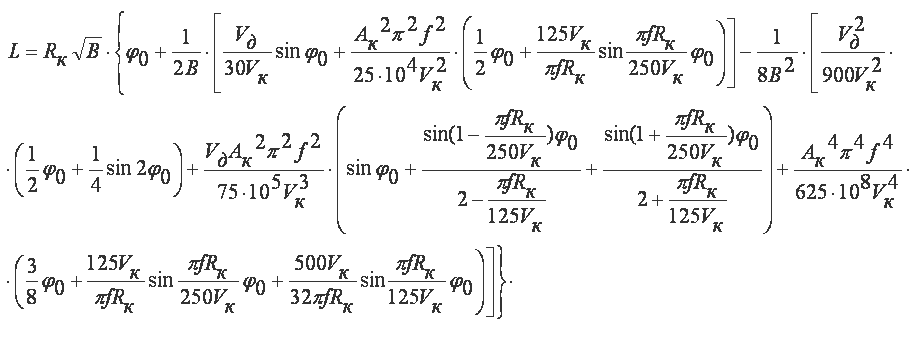

Рисунок 5 -Схема для определения длины дуги контакта единичного зерна с деталью:
а - в случае образования запятообразного среза;
б - в случае образования сегментообразного среза.
Определим значения коэффициентов, стоящих перед скобками, при следующих режимах обработки:
Aк= 1 мм, Vк= 35м/с, Rк=125 мм, f= 25 Гц, Vд= 6м/мин :
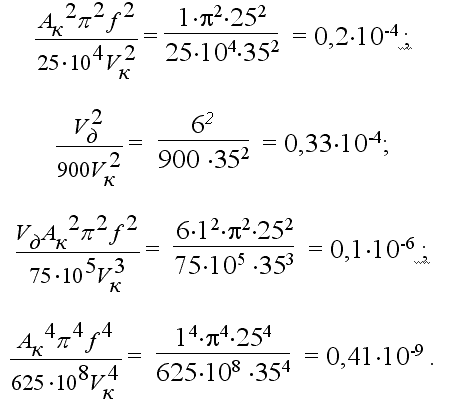
Значениями двух последних коэффициентов можно пренебречь в силу их малого влияния на величину
длины дуги контакта. Таким образом, окончательно уравнение для определения длины дуги контакта
при попутном и встречном характере подачи в случае образования запятообразного среза имеет вид:

Угол контакта зерна круга  можно определить, решив совместно уравнение
траектории движения единичного
зерна (2) и уравнение обработанной поверхности y=tф для случая образования
запятообразного среза,
где tф – фактическая глубина шлифования:
можно определить, решив совместно уравнение
траектории движения единичного
зерна (2) и уравнение обработанной поверхности y=tф для случая образования
запятообразного среза,
где tф – фактическая глубина шлифования:

Для вышеприведенных режимов обработки и tф =0,01мм значение угла контакта составляет
0,012649 рад.
Выясним возможность определения длины дуги контакта единичного зерна шлифовального круга с деталью,
используя для упрощения расчетов в качестве уравнения траектории движения зерна круга – окружность.
Траектория движения зерна круга в пределах угла контакта с обрабатываемой деталью представляет собой
результирующую двух движений: вращения круга и осевого перемещения круга lx за время поворота на
угол контакта (рис.6). Найдем эти составляющие и определим их геометрическую сумму на примере
запятообразного характера среза.

Рисунок 6 – Схема к определению длины дуги контакта единичного
абразивного зерна с обрабатываемой деталью:
1 – дуга контакта единичного зерна с деталью без осевых колебаний круга;
2 - дуга контакта единичного зерна с деталью с учетом осевых колебаний круга
Длина дуги контакта зерна без колебаний шлифовального круга определится по формуле:

Величину осевого перемещения шлифовального круга lx за время поворота на угол контакта определим,
исходя из уравнения траектории движения зерна (2) и ранее найденного значения угла контакта, равна:

Рассмотрим криволинейный треугольник ABA' (рис.6). Развертка этого треугольника на плоскость будет
представлять собой прямоугольный треугольник с известными катетами lx и l0 .
Таким образом длина дуги
контакта единичного зерна круга с обрабатываемой деталью с учетом осевых колебаний круга будет иметь вид:

Ниже (табл.1) приведены результаты расчетов значений длин
дуги контакта единичного зерна
шлифовального круга для плоского шлифования с колебаниями и без колебаний круга при тех же режимах,
что и при выводе формулы (5), а также оценка величины относительной погрешности при расчете длины дуги
контакта по упрощенной траектории.
Таблица 1 – Влияние наличия осевых колебаний шлифовального круга и их частоты на величину длины
дуги контакта единичного зерна с обрабатываемой деталью при плоском шлифовании

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Абразивная и алмазная обработка материалов. Справочник.
Под. Ред. Д-ра техн. наук проф. А.Н. Резникова. М., “Машиностроение”, 1977.
2. Шепелєв А.О. Інтенсифікація процесів шліфування інструментальних матеріалів
кругами із синтетичних алмазів і кубічного нітриду бору. Автореф. Дис... докт. тех. Наук:
05.03.01.- Харків, 2002. – 36с.
3. Матюха П.Г. Теоретические и экспериментальные исследования кинематики
процесса и рельефа круга при алмазно-искровом шлифовании: Дис… канд. тех. наук: 05.03.01.
– Донецк, 1979. – 230 с.




 для встречного шлифования:
для встречного шлифования: 

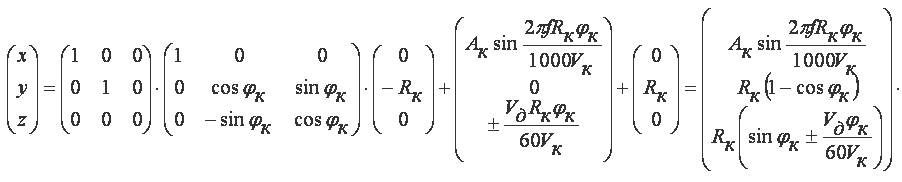


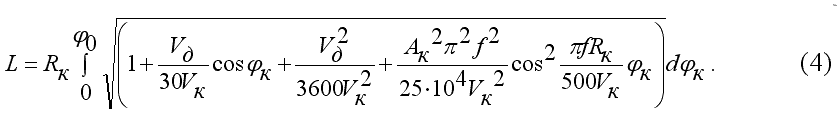
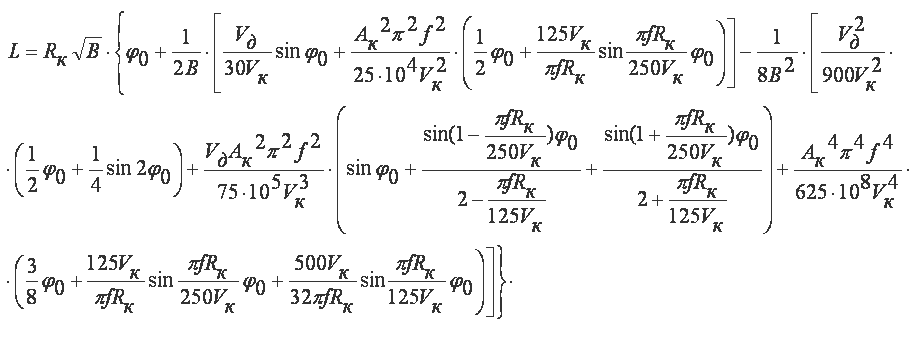

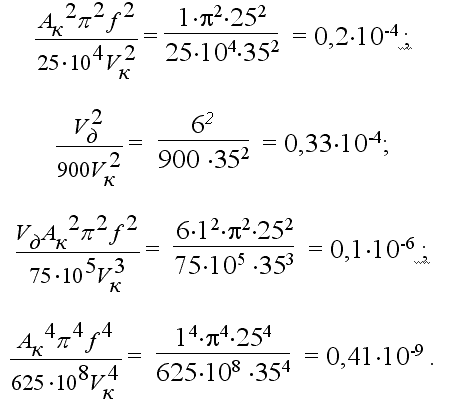

 можно определить, решив совместно уравнение
траектории движения единичного
зерна (2) и уравнение обработанной поверхности y=tф для случая образования
запятообразного среза,
где tф – фактическая глубина шлифования:
можно определить, решив совместно уравнение
траектории движения единичного
зерна (2) и уравнение обработанной поверхности y=tф для случая образования
запятообразного среза,
где tф – фактическая глубина шлифования:





