В настоящее время для применяемых при точении станков характерна высокая степень автоматизации. Системы ЧПУ последних поколений строятся на базе микропроцессорных систем, часто обладающих избыточными вычислительными мощностями. Однако задача определения режимов резания до сих пор решается вручную вне системы ЧПУ. Это связано с тем, что существующие методы подготовки технологической информации мало поддаются формализации и дают неточные результаты, требующие последующей корректировки.

      Неточность основных зависимостей для расчета составляющих сил резания и скорости является причиной недостаточной достоверности математических моделей процесса токарной обработки. Применяемые алгоритмы и программы расчета режимов резания на ЭВМ не дают точных результатов, так как не учитывают реальных условий обработки, состояние и материал резца и детали.

      Практически невозможным остается применение существующих математических зависимостей в алгоритмах автоматизированного определения параметров процесса резания на станках с ЧПУ. Причиной тому является необходимость проведения предварительных механических испытаний образцов обрабатываемых материалов, с целью определения поправочного коэффициента на свойства этого материала. Что касается учета разброса свойств и, соответственно, режущих способностей инструментального материала в пределах одной марки, то в существующих методиках он вообще отсутствует.

      По этой проблеме более двадцати лет ведутся работы на кафедре АПП в ВолгГТУ. Коллективом авторов предложено и обосновано использование для расчета режимов резания формул, использующих сигнал обратной связи, снимаемый непосредственно в зоне резания. Было доказано, что сигнал термоЭДС естественной термопары, инструмент-деталь является комплексным показателем свойств контактирующих материалов. На этой основе были предложены формулы для определения скорости и сил резания (1) :

      Согласно проведенным исследованиям, данные формулы обеспечивают точное соблюдение заданного периода стойкости инструмента, что создает предпосылки для их использования в алгоритмах расчета режимов резания на станках с ЧПУ.

      Определение оптимального режима обработки заготовки на металлорежущих станках состоит в том, чтобы на основе знания свойств заготовки, режущего инструмента, физических законов их взаимодействия в процессе обработки, кинематических и динамических возможностей станка, на котором будет производиться обработка, и свойств системы “станок–приспособление–инструмент–заготовка” назначить такие скорость резания и подачу, которые обеспечат формообразование детали в соответствии с техническими условиями на ее приемку при наименьших затратах общественного труда. При этом глубина резания принимается заданной, определенной на предыдущих этапах проектирования технологического процесса, т. е. каждый проход нормируется отдельно. Это условие соответствует наиболее прогрессивному методу обработки в один проход в каждой операции.

      Каждое из ограничений может быть представлено в виде:

      Т. е. мы получили систему линейных алгебраических уравнений, ограничивающих область допустимых значений n и S.

  Были выведены математические зависимости для следующих технических ограничений, влияющих на режимы обработки.

      Ограничения 1, 2. Устанавливают взаимосвязь расчетной величины подачи с подачей, допускаемой кинематикой станка. Расчетная величина подачи не может быть меньше, чем минимальная и больше, чем максимальная, которая имеется в ряду подач станка.

      Ограничения 3, 4. Устанавливают взаимосвязь расчетной скорости резания с кинематикой станка. Скорость резания не может быть выбрана меньше, чем возможная, исходя из наименьшего числа оборотов станка и больше, чем возможная, исходя из наибольшего числа оборотов станка.

      Ограничение 5. Устанавливает взаимосвязь между скоростью резания, обусловленной принятой стойкостью инструмента, глубиной резания, подачей, с одной стороны, и скоростью резания, определяемой кинематикой станка, с другой стороны.

      Ограничение 6. Устанавливает взаимосвязь расчетной скорости резания с технологически допустимой наименьшей скоростью резания.

      Ограничение 7. Устанавливает взаимосвязь между эффективной мощностью, затрачиваемой на процесс резания, и мощностью электропривода главного движения станка.

      Ограничение 8. Учитывает взаимосвязь расчетных скорости резания и подачи с заданной производительностью станка.

      Ограничение 9. Устанавливает взаимосвязь расчетных скорости резания и подачи с допустимыми по прочности режущего инструмента.

      Ограничение 10. Устанавливает взаимосвязь расчетных скорости резания и подачи с допусoимыми по жесткости режущего инструмента.

      Ограничение 11. Устанавливает взаимосвязь расчетных скорости резания и подачи с точностью обработки, обусловленною жесткостью системы “станок – приспособление – инструмент – деталь”.

      Ограничение 12. Устанавливает взаимосвязь расчетных скорости резания и подачи со скоростью и подачей, допускаемыми требованиями, предъявляемыми к шероховатости обработанной поверхности.

      Графически система ограничений представлена на следующем рисунке.

Рисунок 1 - Графическая интерпретация системы технических ограничений

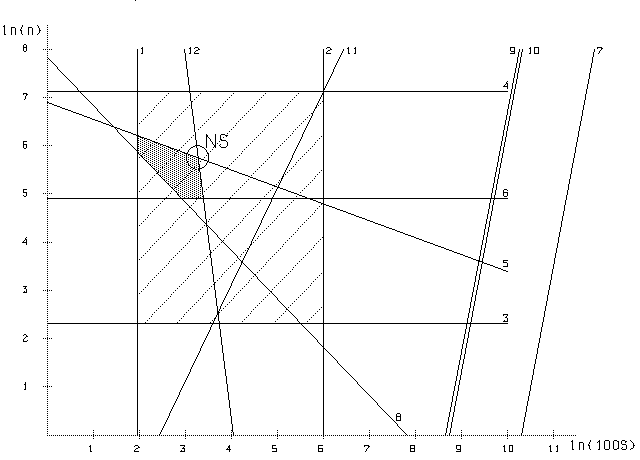
      Редкой штриховкой обозначена область значений n и S, допускаемых кинематикой станка. Частой штриховкой обозначена область значений n и S, удовлетворяющая всем техническим ограничениям.

      Для ограничений 5, 7, 9–12 величина bi есть функция термоЭДС. В процессе обработки величина термоЭДС изменяется, следовательно, изменяются и границы исследуемой области. Задача заключается в нахождении точки оптимальных значений скорости резания и подачи, удовлетворяющих техническим ограничениям, а также в определении траектории этой точки в зависимости от текущего значения термоЭДС.

      Глубина резания, геометрия инструмента и его материал предполагаются постоянными и известными величинами. Проектирование реальных операций обработки резанием в этом случае необходимо проводить последовательно в несколько этапов, включающих назначение инструмента (материала режущей части и геометрических параметров); разбиение общего припуска на каждый рабочий ход и назначение технологических требований для каждого из этих рабочих ходов; определение оптимальных режимов для каждого рабочего хода с помощью решения задачи линейного программирования.

      Допустимая область решений задачи линейного программирования является выпуклым многогранником с конечным числом вершин. Это значит, что экстремум целевой функции всегда является глобальным и достигается в одной из вершин такого многогранника. Поэтому нахождение экстремума задачи производится направленным перебором крайних точек области определения задачи или вершин многогранника (точка NS на рисунке).

      С этой целью предлагается использовать симплекс-метод, как наиболее отработанный и распространенный метод решения задач линейного программирования, позволяющий найти крайнюю точку допустимой области (или вершину многогранника) и определить, является ли она точкой экстремума целевой функции. Конечность метода поиска экстремума для задачи линейного программирования является важной его особенностью, так как методы решения задач нелинейного программирования не являются конечными, а, следовательно, дают лишь приближенные значения.

      Особое внимание в работе уделено исследованию дрейфа точки NS, имеющему место в процессе резания. При чистовой и получистовой обработке экстремум в большинстве случаев находится на пересечении линии 5 (ограничение по периоду стойкости инструмента) и линии 12 (ограничение по заданной величине шероховатости обрабатываемой поверхности). В случае, когда эта точка не удовлетворяет условию 6 (обработка сдвигается в зону наростообразования), рекомендуется пересмотреть величину периода стойкости инструмента.

      Величина термоЭДС не входит в формулу определения точности обработки, следовательно, линия 12 статична и зависит только от заданной шероховатости. Период же стойкости инструмента весьма чувствителен к изменениям, происходящим в зоне стружкообразования и регистрируемым датчиком термоЭДС. Это значит, что линия 5 будет перемещаться параллельно самой себе. Таким образом, точка NS будет “скользить” вдоль прямой 12.

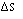      С помощью программы “Regime”, разработанной авторами, на ПЭВМ был смоделирован процесс резания и определены крайние положения точки экстремума целевой функции. На основе этих данных был предложен метод поднастройки параметров процесса резания и рассчитаны оптимальные значения констант и , корректирующих соответствующие параметры в процессе обработки. Предлагаемый метод заключается в коррекции режимов обработки в зависимости от сигнала обратной связи из зоны стружкообразования. В качестве такого сигнала принимается величина термоЭДС естественной термопары “инструмент-деталь”, которая используется не как традиционная характеристика уровня температур в зоне резания, а как интегральный показатель физико-механических свойств контактирующих пар.

      Первоначально режим обработки рассчитывается исходя из термоЭДС пробного прохода Eпр. В процессе резания величина термоЭДС должна поддерживаться на постоянном уровне. С этой целью при ее повышении, что свидетельствует об ухудшении условий резания, подача остается неизменной, а частота вращения шпинделя циклически уменьшается на величину . При понижении термоЭДС режим корректируется в обратную сторону.

      На основе математической модели разработаны алгоритмы решения задачи линейного программирования и автоматического расчета оптимальных параметров режимов резания для системы ЧПУ. Оба алгоритма реализованы на ПЭВМ и показали высокую производительность при минимальных затратах времени.

      Применение математической модели и предложенных алгоритмов ее реализации на производстве позволит существенно сократить основное технологическое время операций точения, время простоя, связанное с поломками инструмента, повысить живучесть гибких производственных систем за счет увеличения времени безотказной работы.