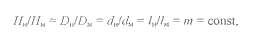
Физическое моделирование – один из методов научных исследований, предполагающий замену изучения интересующего натурного образца объекта или реализуемого с его помощью технологического процесса проведением экспериментов на модели с обеспечением условий протекания явлений, имеющих ту же физическую природу.В данной работе приведены краткие сведения из теории подобия.критерии газодинамического подобия.
Как известно, гидродинамические, тепловые и химические процессы, протекающие в металлургических агрегатах, характеризуются высокими температурами, воздействием агрессивных шлаков и выделением большого количества вредных газов и абразивных пылевидных частиц. Выполнение экспериментальных работ, связанных, прежде всего, с изучением явлений тепломассопереноса, в таких условиях практически невозможно по соображениям безопасности персонала. Кроме того, серьезным препятствием для проведения исследований на действующих промышленных агрегатах является такой фактор, как потеря производственного времени.
В подобной ситуации, а также при создании новой техники на стадии проработки конструкции проектируемой машины или агрегата наиболее приемлемым способом решения возникающих проблем следует считать применение физического моделирования.
Физическое моделирование - один из методов научных исследований, предполагающий замену изучения интересующего натурного образца объекта или реализуемого с его помощью технологического процесса проведением экспериментов на модели с обеспечением условий протекания явлений, имеющих ту же физическую природу.
2.1. Краткие сведения из теории подобия
Две физические системы будут геометрически подобными, если между их соответствующими линейными размерами существует постоянное соотношение
где in - линейный масштаб, показывающий во сколько раз размеры модели уменьшены по сравнению с размерами натуры
Следует отметить, что у геометрически подобных систем должны быть постоянными соотношения площадей и объемов:
Кинематическое подобие подразумевает подобие полей скоростей и ускорений натуры и модели, выполняемое в том случае, когда скорости у и им и ускорения ан и ям в сходственных точках натуры и модели находятся в одинаковых соотношениях:
Вполне понятно, что кинематическое подобие обязательно включает в себя геометрическое подобие.
При динамическом подобии все соответствующие силы, действующие в подобных точках натуры и модели, имеют одинаковые направления, а их отношения постоянны, т. е. силовые многоугольники, построенные для натуры и модели, должны быть геометрически подобными.
В соответствии со сложившейся терминологией теории подобия отношения величин в пределах изучаемой физической системы принято называть вариантами или критериями подобия.Основополагающие признаки подобия процессов (явлений) сформулированы в трех теоремах.
Согласно первой теореме подобными процессами (явлениями) считаются те, которые имеют идентичные соответствующие критерии подобия. Эта теорема позволяет выделить физические величины, которые нужно измерять при проведении опытов. К ним относятся величины, входящие в состав критерия.
Вторая теорема подобия, получившая название тс-теоремы, отражает тот факт, что практический интерес представляют не сами критерии (числа) подобия, а соотношения между ними (о чем подробно будет сказано ниже). Данная теорема предполагает обобщение результатов измерений в виде дифференциальных уравнений, в которых переменными являются критерии подобия. Благодаря этому сокращается число переменных и упрощается обработка получаемых результатов измерений.
Следует отметить, что названные две теоремы не позволяют установить необходимые и достаточные условия динамического подобия. Указанные условия оговорены третьей теоремой подобия, в соответствии с которой два явления будут считаться подобными, если они имеют идентичные определяющие критерии (числа) подобия, составленные из параметров систем, а также подобные условия однозначности.
2.2. Критерии гидрогазодинамического подобия
Условием гидрогазодинамического подобия является равенство на модели и в натуре отношений всех действующих на физическую систему сил: тяжести, давления, инерции, поверхностного натяжения. На практике достичь подобия всех сил не удается, что связано с физическими особенностями этихсил. Поэтому приходится рассматривать частные случаи, для которых из всей совокупности действующих сил выделяется одна, считающаяся при данных условиях эксперимента преобладающей [4].
Соотношения различных сил устанавливаются числами (критериями) гидрогазодинамического подобия, имеющими соответствующие названия.
Критерий Рейнолъдса представляет собой отношение сил инерции к силам внутреннего трения:
где v – скорость движения среды; d – характерный геометрический размер; р – плотность среды; г| – динамическая вязкость среды.
Критерий Фруда характеризует соотношение сил инерции и сил тяжести:
где g – ускорение силы тяжести
Критерий Эйлера представляет собой отношение разности сил статического давления к силе инерции:
где АР – разность сил статического давления, вызывающего движение среды.
Критерий Маха представляет собой отношение скорости движения газа в определенной точке к скорости распространения звука в этой же точке:
где с – скорость распространения звука.
Поскольку безразмерные комплексы Re, Fr, Sh, M в своем составе имеют скорость v, то они обладают свойством взаимозаменяемости, в связи с чем их можно умножать или делить друг на друга, получая при этом новые критерии.
Перемножив критерии Рейнольдса и Эйлера, получают критерий Ла-гранжа, который характеризует отношение сил давления к силам вязкости:
где РО и VQ – масштабные (базовые) значения давления и скорости потока.
Существуют и другие критерии, которые относятся к частным случаям: число Архимеда, число Прандтля и другие.
2.3. Метод анализа размерностей
Метод анализа размерностей применяется тогда, когда неизвестны уравнения, определяющие исследуемый процесс. Этот метод позволяет обработать, а затем и обобщить данные, полученные опытным путем.
Все физические величины, входящие в определяющее уравнение и являющиеся существенными для изучаемого процесса, подразделяются на две группы.
К первой группе относятся величины, размерности которых являются первичными (базовыми): масса, длина, время и температура. Из таких величин нельзя образовать безразмерные комплексы.
Во вторую групп)7 входят величины, размерности которых компонуются из размерностей базовых величин: площадь, объем, скорость, ускорение, давление и т.д. Величины этой группы позволяют составлять при различных комбинациях безразмерные комплексы – числа подобия (критерии).
Связь между числами физических параметров первой и второй группы, характеризующих течение процесса, позволяет установить я-теорема, составляющая основу теории метода анализа размерностей.
Данная теорема, доказанная в 1911 г. Г. А. Федерманом, может быть сформулирована следующим образом. Всякое уравнение, выражающее некоторую физическую закономерность и связывающее собой / величин, из которых k имеют независимые размерности, можно преобразовать в уравнение, связывающее (i-k) независимых безразмерных комплексов (критериев), составленных из физических величин.
Критериальное уравнение может быть представлено как
В качестве примера использования я-теоремы при составлении критериального уравнения рассмотрим последовательность вычислений, которую необходимо выполнить в случае установления зависимости для числа Рейнольдса.
Число Рейнольдса является критерием, определяющим режим движения, который зависит от средней скорости v, динамической вязкости ц и плотности р жидкости, а также от диаметра d трубы. Нетрудно заметить, что определяющее уравнение в данном случае связывает четыре физические величины/(и, ц, р, d) = 0, а минимальное число первичных размерностей, из которых образованы размерности всех четырех параметров уравнения, равнотрем (размерности массы, длины и времени). Таким образом / = 4, & = 3. Отсюда в соответствии с тс-теоремой следует, что число безразмерных параметров, характеризующих явление, i-k = 4-3 = 1.
Составляя произведение степеней параметров и применяя к нему условие нулевой размерности, получаем
где х, y,z,k – показатели степени, подлежащие определению.
Учитывая, что размерности параметров могут быть представлены в виде [v] = Li~l\ [\Ji]=ML~ т"1; [p]=ML 3; [d] = L, составленное произведение степеней параметров при замене их размерностями можно преобразовать в выражение (Li-1)* (MrV1/ (ML'3)2 (Lk) = A/W
Приравняв показатели степеней у одинаковых оснований в левой и правой частях полученного выражения, можно составить систему трех уравнений
Решение этой системы уравнений дает результат x = -y9x = z',x = k. Тогда искомый безразмерный комплекс П = (vpJ/ц)"7, где т может иметь любое значение, отличающееся от нуля. При т = 1 получаем число Рейнольдса П = Re = (vprf/ц).
Таким образом, метод анализа размерностей позволяет находить числа подобия при отсутствии математического описания исследуемого явления. Для этого необходимо только точно установить параметры, от которых зависит данное явление. Однако следует отметить, что для полной уверенности в справедливости результатов выполненного анализа необходимо проведение дополнительной опытной или теоретической проверки. Значимость получаемых результатов будет зависеть от глубины проникновения в суть исследуемого вопроса и от опыта практического использования теоретических положений [19, 90].
2.4. Основные этапы физического моделирования
Физическое моделирование как метод исследования включает в общем случае пять основных этапов [56]: постановку задачи; вывод и анализ условия подобия; выбор конструкции и расчет параметров модели объекта исследования; проведение экспериментов на модели; обработка полученных результатов.
При постановке задачи необходимо исходить из того, что главная цель моделирования заключается в изучении основных закономерностей исследуемого процесса, а результаты, полученные в ходе эксперимента, после обобщений могли бы быть использованы в реальных промышленных условиях. Достичь намеченной цели можно в том случае, если проведение опыта будет осуществляться с учетом основных положений теории подобия.
Цель исследования в каждом конкретном случае может быть разной: от стремления получить эмпирические данные, полезные для использования в инженерной практике или позволяющие выполнить проверку теоретических положений, до изучения в общих чертах физической картины разработанного процесса. Однако даже когда не требуется получение особо точных результатов (приближенное или качественное моделирование), необходим анализ условий подобия. На этом этапе на основании совокупности выбранных критериев рассматривается возможность упрощения условий подобия. При этом оцениваются численные значения критериев и определяется их значимость, что позволяет часть из них отнести к разряду несущественных, т.е. не требующих обеспечения равенства для модели и оригинала.
Выбор конструкции модели во многом зависит от характерных особенностей моделируемого процесса, а также от того, в каком виде необходимо получить интересующую информацию. К примеру, если исследуемый процесс обусловлен интенсивным движением жидкостных потоков и в итоге требуется получение картин их распределения в различных зонах перемешиваемой ванны, модель конструктивно должна обеспечивать возможность визуального контроля и фотографирования потоков.
Модель изготавливается геометрически подобной натуральному образцу по внутренним контурам. При этом используются всевозможные материалы, но чаще всего применяют органическое стекло.
Подготовка модели к проведению исследований заключается в выборе варианта рационального размещения применяемой аппаратуры, обеспечении возможности быстрой замены моделирующей расплав жидкости, поддержании требуемой освещенности объектов, подлежащих фотографированию, и так далее.
Проведению исследований на модели предшествует планирование эксперимента, настройка регистрирующей аппаратуры и при необходимости тарировка преобразователей измерительных систем.
Собственно физическое моделирование в зависимости от решаемых задач может проводиться по уже известным или специально разработанным методикам с применением широкого набора контрольных датчиков и электронных приборов, предназначенных для регистрации параметров процессов, протекающих в моделях.
Обработку полученных результатов осуществляют с использованием методов математической статистики и привлечением средств вычислительной техники. При этом необходимо выделить впервые зафиксированные данные, попытаться дать им полное объяснение и сопоставить их с уже известными результатами [20].
После обобщения данные должны быть представлены в виде таблиц и графиков.
[4].Большаков В.А.,Попов В.Н. Гидравлика. Общий курс:Учеб.для вузов. – К.:Вища шк.,1989. – 215с.
[19].Дейч М.Е.,Зарянкин А.Е.Гидрогазодинамика:Учеб. пособие для вузов. – М.:Энергоатомиздт,1984. – 384с.
[90].Седов Л.И. Методы подобия и размерности в механике. – М.:Наука,1981. – 447с.