УДК
621.311.153.22:519.2.001.24ІМІТАЦІЯ КОРЕЛЬОВАНИХ ВИПАДКОВИХ ПРОЦЕСІВ В ЕЛЕКТРИЧНИХ МЕРЕЖАХ МЕТОДОМ ЕЛЕМЕНТНИХ ПРОЦЕСІВ
Курінний Е.Г., Циганкоеа Н.В.
Праці Донецького державного технічного університету "Електротехніка і енергетика".- Донецьк, випуск 17, 2000.- С. 142-145
Донецький державний технічний університет
Іе
d@,dgtu.donetsk. иа
The problem of imitation of system of correlative random processes has been considered. It has been suggested to imitate every process as the sum of easy element processes some part of which is connection. The method of imitation can be used for decision of unlinear problems of electrical engineering.
Постановка задачі.
Широкий клас задач електропостачання промислових підприємств є нелінійними. По-перше, це зумовлено тим , що параметри режиму є векторами. По-друге, вплив цих параметрів на електроприймачі і мережі залежить від відповідних втрат потужності, що потребує аналізувати квадрати процесів. Наприклад, це притаманне такому показнику ЕМС, як доза флікеру [І], який визнано міжнародною спільнотою - на відміну від дози коливань напруги [2]. По-третє, деякі показники являють собою нелінійні функції випадкових аргументів, як, наприклад, функція поділу двох величин, яка відтворює питомі витрати енергоносіїв і тангенс фі.Література по методам імітації окремих випадкових процесів дуже велика, проте публікації не містять даних про імітацію корельованих процесів. Метою роботі є розробка метода імітації корельованих процесів Х(t) і У(і) відповідно до типової задачі електропостачання, яка полягає в підсумовуванні навантажень електроприймачів.
Для визначеності розглядається система двох нормальних стаціонарних процесів, яка більш за все зустрічається у практичних задачах: наприклад, процеси активної і реактивної потужностей викликають нагрів елементів мережі, а також втрати і коливання напруги, які негативно впливають на електроприймачі. Розповсюдження результатів на більшу кількість процесів і інші імовірнісні розподіли, які відповідають схемі суми, не викликає труднощів.
Ідея методу. Для імітації процесів Х(і) і У(t) застосуємо метод елементних процесів (ЕП) [З]. Він полягає в тому, що реалізація процесу Х(t) з заданою кореляційною функцією KC ( t ) знаходиться як сума п незалежних ЕП х(t), кожний з яких має кореляційну функцію
![]() (1)
(1)
Імовірнісні розподіли ЕП не мають значення, бо при підсумовуванні великої кількості п процесів розподіл суми збігається з нормальним. Такім же чином знаходиться і реалізація Y(t).
Для отримання ЕП застосовуються послідовності випадкових чисел x, які виробляються датчиком випадкових величин. Ці послідовності піддаються перетворенням Lx і Lу за умовою відтворення кореляційних функцій kx(t) і ky(t) відповідних ЕП.
Ідея методу, що пропонується, полягає в тому, що т із п
послідовностей випадкових чисел x 1,...,x
m приймаються
однаковими для обох процесів: зі знаком, який збігається зі знаком заданого
коефіцієнту кореляції R. Відповідні “парні” ЕП (знак ~)
![]() ,...,
,...,![]()
![]() ,...,
,...,![]() будуть"корельованими, а
останні процеси Хm+1,...,C n
і Ут+1,--Уп- ні.
будуть"корельованими, а
останні процеси Хm+1,...,C n
і Ут+1,--Уп- ні.
Наявність парних ЕП робить процеси Х(t) і У(t) також корельованими. Задача полягає у визначенні кількості т парних ЕП.за умовою відтворення R.
Кількісні співвідношення. Як відомо [4 ], випадковий процес, який надходить на вхід системи зі сталою часу Tc, можна розглядати як білий шум за умовою, що його стала кореляції буде на порядок менше, ніж Tc. Генератор випадкових чисел дає послідовності з нормованою кореляційною функцією у вигляді прямокутного трикутника з вершиною одиниця і основою, яка дорівнює інтервалу часу D між суміжними значеннями послідовності. Стала кореляції t kx такого процесу дорівнює D /2, тому послідовність x можна вважати білим шумом,якщо
D <<2Tc , (2)
Оскільки імітується декілька процесів, то в нерівності (2) береться найменша стала часу.
Стандарти s x усіх послідовностей однакові. За умовою (1) параметр білого шуму становить:
c =2s x 2t kx =s x 2D , (3)
Кореляційна функція білого шуму
kx (t )=p cd (t ) (4)
визначається через дельта-функцію d (t ).
Для подальшого скористуємося фундаментальним положенням теорії ймовірностей про те, що стаціонарний процес х(t) є результат проходження білого шуму через умовну лінійну систему з ваговою gx(t) і амплітудною частотною Ax(w) функціями, параметри яких залежать від кореляційної функції kx(t) або відповідної спектральної щільності Sx (w ).
Оскільки параметр с є спектральною щільністю білого шуму, вигляд умовної системи зручно вибрати по амплітудній частотній функції згідно з рівнянням
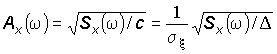 (5)
(5)
Суттєво, що незалежно від способу отримання ЕП, їх зв'язок з білим шумом визначається інтегралами Дюамеля
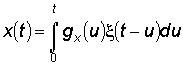 ,
, 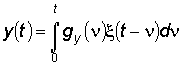 , (6)
, (6)
Згідно з формулою (6.2.10) з [4] знайдемо кореляційний момент між парними ЕП в стаціонарному стані
(при t® ¥ ):
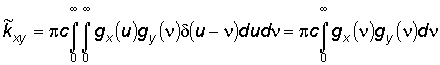 (7)
(7)
Згідно з (1) стандарти ЕП:
![]() ,
, 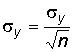 ,
,
в ![]() менше за стандарти
s x і s
у шуканих процесів.
менше за стандарти
s x і s
у шуканих процесів.
Коефіцієнт кореляції між парними ЕП
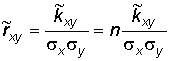 . (8)
. (8)
Перейдемо до характеристик шуканих процесів. Позначення сум приймемо за способом Гауса:
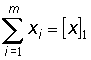 ,
, 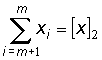 .
.
Реалізації шуканих процесів знаходяться шляхом підсумовування ЕП зі своїми знаками:
X=[ x] 1+[ x] 2, Y=± [ y] 1+[ y] 2.
Взаємні кореляційні функції між
X і
![]() дорівнюють нулю, бо між
відповідними білими шумами x ,< не має зв'язку, а тому
кореляційна функція суми ЕП x(t) збігається з заданою Kx(t).
Покажемо, що це виконується і для другого
процесу. Дійсно, оскільки у і
дорівнюють нулю, бо між
відповідними білими шумами x ,< не має зв'язку, а тому
кореляційна функція суми ЕП x(t) збігається з заданою Kx(t).
Покажемо, що це виконується і для другого
процесу. Дійсно, оскільки у і
![]() не корельовані, то згідно з
теоремою про кореляційну функцію суми або різниці некорельванік процесів знайдемо
не корельовані, то згідно з
теоремою про кореляційну функцію суми або різниці некорельванік процесів знайдемо
![]() .
.
Позначивши через M операцію знаходження математичного очікування, визначимо взаємний кореляційний момент:
![]() .
.
У цьому виразі лише математичне очікування добутку ![]() 1
сум парних ЕП відрізняється від нуля. В свою чергу, у останньому добутку лише добутки
1
сум парних ЕП відрізняється від нуля. В свою чергу, у останньому добутку лише добутки
![]() з однаковими індексами
мають однакові кореляційні моменти, які визначаються формулою (7).Тому остаточно
знайдемо
з однаковими індексами
мають однакові кореляційні моменти, які визначаються формулою (7).Тому остаточно
знайдемо
![]()
За визначенням коефіцієнт взаємної кореляції між процесами
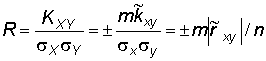 , (9)
, (9)
де враховане співвідношення (8).Воно відноситься до додатних ЕП, тому в формулі (9) потрібно брати абсолютне значення коефіцієнта кореляції.
Формула (9) дає змогу знайти шукану кількість
![]() . . (10)
. . (10)
Якщо імітуються процеси з однаковими нормованими кореляційними функціями, то у цьому випадку
![]() ,
, ![]() =1 а потрібна кількість
парних ЕП m=nï Rô .
=1 а потрібна кількість
парних ЕП m=nï Rô .
Реалізація методу. Імітація стаціонарних ергодичних процесів може бути здійснена як “по реалізації” великої тривалості, так і “по ансамблю” з великою кількістю N реалізацій. В обох випадках потрібно вилучити з розгляду початковий інтервал Tn часу, в межах якого відбувається перехідний процес від нульових початкових умов. Тривалість цього інтервалу дорівнює 5-6 найбільших сталих часу Тс.
Імітація замінює експеримент, тому якість відтворення характеристик процесів оцінюється відомими методами математичної статистики: по критеріям згоди - для статистичних (знак Ù ) розподілів і довірчим інтервалам - для кореляційних функцій і коефіцієнтів кореляції. Оскільки нульове і одиничне значення коефіцієнту кореляції відтворюється точно, то найбільшу похибку слід очікувати при І К 1 =0,5.
Імітація по ансамблю має деякі переваги. По-перше, з умови визначення кореляційної функції на інтервалі значень аргументу від 0 до t max тривалість імітації достатньо брати рівною Tn+t max. По-друге, зріз по ансамблю буде кратний величині D , тому помилка від дискретності часу зникає. По-третє, метод імітації по своїй суті не гарантує відтворення характеристик для кожної реалізації, тому є вірогідність появи реалізації, яку потрібно виключити з розгляду. При імітації по ансамблю це практично не позначається на результаті усереднення, бо ця ймовірність дуже мала, а значення, які дуже відрізняються від інших, можна виключити згідно із принципом практичної впевненості. Довірчу ймовірність -Ед звичайно приймають рівною 0,9, що відповідає однаковим імовірностям виходу за верхню і нижню межі довірчого інтервалу: по 0,05.
Висновки.
1. Введення парних елементних процесів дозволяє з заданою похибкою імітувати систему взаємно корельованих випадкових процесів.
2. Систему випадкових процесів доцільно імітувати по ансамблям їх реалізації.
ЛІТЕРАТУРА
1. Flickermeter. Functional and design specification.-Geneva: IEC Report, 1986, Publication 868.- p.31.
2. ГОСТ 13109-87. Злектрическая знергия. Требования к качеству злектрической знергии в злектрических сетях общего значення.-Введ.01.01.89.
3. Куренный Э. Г., Дмитриева Е.Н. Статистическое моделирование нормальних случайных процессов в заводских электрических сетях. -Изв. АН СССР. Энергетика и транспорт, 1977, №5.- С.128-140.
4. Тихонов В.И. Статистическая радиотехника. -М.: Советское радио, 1966. - 678 с.
5. Пугачев В.С. Теория вероятностей и математическая статистика.-.М.: Наука, 1979. - 496 с.