Дмитрієва О.М.,Лютий О.П. МЕТОД СИМЕТРУВАННЯ ДЛЯ ВИДІЛЕННЯ СТАЦІОНАРНИХ КОМПОНЕНТ РЕЖИМІВ ВИРОБНИЦТВА І ВИТРАТ ЕНЕРГОНОСІЇВ | Библиотека Баштинской Ю.Н.
К библиотеки

УДК 621.3.003
МЕТОД СИМЕТРУВАННЯ ДЛЯ ВИДІЛЕННЯ СТАЦІОНАРНИХ КОМПОНЕНТ РЕЖИМІВ ВИРОБНИЦТВА І ВИТРАТ ЕНЕРГОНОСІЇВ

Дмитрієва О.М.
Донецкий державний технічний університет
Лютий О.П.
ВАТ «Дніпроспецсталь»

Наукові праці ДонНТУ - Електротехніка і енергетика - 2004 - випуск 79

          It is developed the method of definition of efficient regime of power-consumption by experimental data. Range norms of production's output and consumpjion of power-bearers are established. It is offered to define the underproduction of production and over-expenditure of power-bearers with respect of range norms.

         Постановка задачі. В усталеному ритмі виробництва є неминучими стаціонарні коливанкя продуктивності й витрат енергоносіів відносно іх середніх значень. Ці коливання потрібно враховувати при аналіі параметрів режиму. Окрім стаціонарних бувають i нестаціонарні коливання, які виникають внаслідок роботи з недовантаженням, порушень стану обладнання, тощо. Вони призводять до невиправданого погіршення техніко-економічних показників виробництва,а тому повинні бути виключені з розглядання.
         Ідею виділення стаціонарної компоненти (складовоі) було висловлено в [1]: імовірнісний розподіл тривалостей циклу роботи повинен бути нормальним. Це означає, що малі значення тривалостей циклу потрібно залишити, а великі - скорегувати з таким розрахунком, щоб кінцевий розподіл став нормальним. В [2] було запропоновано кількісну оцінку границі симетрування: по половині функціі розподілу, а не по максимуму щільності розподілу, як у [1].
         Однак у цих роботах розглядався лише одномірний випадок, хоча процеси енергоспоживання не можна розглядати у відриві від виробництва: так, зменшення енергоспоживання ще не означає енергозбереження, якщо воно веде до недовипуску продукціі. Метою статті є узагальнення методу симетрування на систему параметрів режиму. Для визначеності викладення дається на прикладі одного з виробництв, для якого основними енергоносіями є газ i електроенергія.
         Стаціонарний режим. Для режиму проектноі продуктивності встановлюються норма VTн випуску продукції за базовий інтервал часу T (тривалість технологічного циклу, зміну, добу, місяць, рік), а також норми питомих витрат ρн електроенергії і gн газу , які дозволяють розраховувати норми

WTн = ρнVTн,          GTн = gнVTн

витрат енергоноспв. Ці норми назвемо «точковими», осильки вони не враховують cтаціонарні коливання.
          Будемо розрізняти диференційні й інтегральні параметри режиму. До перших відносяться активна потужність p , яка характеризує швидкість споживання електроенергії. Аналогічно введемо поняття потужності газу x і швидкості y виробництва. Інтегральні параметри визначаються за заданий період Т часу. До них відносяться об’єм VT випуску продукції, витрат WT електроенергії і GT газу . Зв'язок між параметрами визначається інтегралами

VT= T0∫ y(t)dt,      WT= T0∫ p(t)dt,      GT= T0∫ x(t)dt/

          На параметри впливає багато факторів, кожен з яких не є вирішальним. Тому в стаціонарному режимі параметри маютъ нормальні розподіли. Система випадкових диференційних параметрів характеризується середніми значеннями ус, рс i xс, стандартами σy, σp, σx , а також кореляційними функціями ky(τ), kp(τ),kx(τ). Останні в практиці звичайно апроксимуються виразами виду

k(τ)=(1/2)σ2[exp(-α-jω0) |τ| +exp(-α+jω0) |τ| ],      (1)

          aбо їх сумою, де α і ω0 - параметри, j=√(-1) .
          Зі збільшенням базового інтервалу середні значення

VTc = ycT,     WTc = pcT,      GTc = xcT.          (2)

          Інтегральних параметрів у іменованих одиницях зростають пропорційно середнім значенням диференційних параметрів. З врахуванням формул (11.58) з [2] і (6.35) з [3] для процесу y(t) з кореляційною функцією (1) отримаємо стандарт випуску продукції

.          (3)

          3i зростанням T стандарт також зростає, але повільніше, ніж середнє значення, оскільки відношення σVT до VTc при T→∞ прямує до нуля. Аналогічні (3) формули слушні i для стандартів σWT, σGT витрат енергоносіїв.
          Перейдемо до системи відносних одиниць (в.о.), у якій до базових величин інтегральних параметрів додамо точкові норми диференційних параметрів:

yн=VTн/T,     pн=WTн/T,      xн=GTн/T.          (3)

які не залежать від базового інтервалу.
          Зручність системи полягае в тому, що у в.о. (індекс *) середні значення диференційних та інтегральних параметрів співпадають i також не залежать від Т:

VTc*=VTc/VTн=yc/yн=yc*,     WTc*=pc*,      GTc*=xc*.          (4)

          Вираз (3) у в.о. приймае вигляд

.

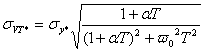          Звідси випливає, що стандарт зменшується зі зростанням базового інтервалу.
          Для нормальної випадкової величини границі діапазону практично достовірних її значень приймаються симетричними відносно середнього значення на відстані ±β , де статистичний коефіцієнт β визначається через задану імовірність виходу величини за границі діапазону. Звичайно імовірність приймають рівною 0,05, якій відповідає β = 1.65.
          Допустимі діапазони статистичних коливань становлять:

VT*max,min=yc*±βσVT*,     WT*max,min=pc*±βσWT* GT*max,min=xc*±βσGT*.          (5)

          Вирази (5) визначають «діапазонні» норми для параметрів режиму. Лише при діапазонні норми вироджуються у точкові. Це означає, що норми для проектного режиму можна використовувати лише при великих значеннях базового iнтервалу.
          Випуск продукції. Початковими можуть бути як диференційні, так i інтегральні параметри режиму. Як приклад розглянемо добові параметри, опускаючи індекс Т у позначеннях. На рис. 1 показано експериментальні графіки (індекс ~) зміни випуску продукції i витрат електроенергії й газу за один місяць.


Рисунок 1

          Енергоспоживання зумовлене процесом виробництва, тому виділення стаціонарного режиму треба виконувати в дві стадії: спочатку симетрувати процесс (t) , а потім зв'язані з ним процеси енергоспоживання.
          Розглянемо першу стадію. Відхилення ординат процесу (t) від гіпотетичного середнього значення Vc у бік більших значень по суті треба віднести до стаціонарних - за винятком тих, що виходять за границю обмеження; якщо вона є. Ідея методу полягає в наступному: експериментальні дані п , що перевищують середнє значення, зберігаються. 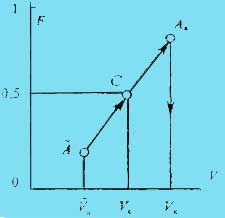В області ж малого випуску продукції замість експериментальних приймаються симетровані значення к, які забезпечують центральну симетрію функції розподілу F(V) відносно центра С симетрування з координатами (Vc ; 0,5). На рис. 2 хід симетрування показано строками для однієї точки Ã , абсциса n якої менша за середнє значення. Через точки Ã i С проводиться пряма лінія. Шукана точка Aк знаходиться на однаковій відстані AкC = ÃC від вертикалі Vc, що і точка Ã. Звідси витікає, що абсциси симетрованих значень визначаються за формулою

Vк = 2Vc - п .    (6)

Рисунок 2

          Визначимо середнє значення. В [1] його запропоновано приймати по максимуму щільності розподілу випуску продукції. Для цього не можна безпосередньо використовувати гістограму, оскільки вона має незакономірні коливання, що не дозволяеє визначати положення максимуму. Тому гістограму потрібно вирівнювати теоретичною функцією: наприклад, згідно з бета-розподілом. Однак положення максимуму визначається числовими характеристиками масиву експериментальних даних, які залежать не тільки від абсцис праворуч від максимуму, a i від абсцис ліворуч. Чим більші нестаціонарні зменшення випуску продукції тим більше зменшується максимум. Ця неоднозначність виключає застосування щільності розподілу.

          В [2] середнє значення знаходиться за статистичною функцією розподілу - при ординаті 0,5. Тут виникає зовсім невелика неоднозначність. Так, якщо кількість N ординат є непарною, то між двома абсцисами _ i +, для яких функція розподілу менша i більша за 0,5, положення середнього значення залежить від того, як провести цю функцію через дві ординати: східчасто або лінійно. Якщо N є парною, то горизонталь 0,5 попадає на ординату для абсциси N/2, але приймати цю ординату за середнє значення не можна, оскільки вона не обов'язково буде знаходитися на однаковій відстані від сусідніх ординат. Опускаючи символ * в.о., для однозначності приймемо

Vc=(_++)/2.     (7)

де при парній N ординати у дужках приймаються для абсцис N/2 + 1. Наприклад, для графіка на рис. 1, де є тридцять діб, візьмемо ординати за 14-те i 16-те числа: 1,013 i 0,934. Тоді середнє значення буде дорівнювати 0,934.
          Стандарт σV гіпотетичного розподілу визначається по об'єднаному масиву значень п ,Vк , який має середнє значения (7). Якщо присутні нестаціонарні відхилення, цей стандарт має бути меншим за стандарт V усього початкового масиву .
          Знайдені середнє значення i стандарт визначають нормальний розподіл випуску продукції, а рівняння (5) дають границі зміни об'емів випуску продукції у стаціонарному режимі. Провали за нижню границю визначають недовідпуск продукції через нестаціонарні відхилення, а викиди -перевищення плановї продуктивності.
          Втрати енергоносіїв. Ti ж caмi міркування щодо (7) дозволяють визначити середні значення витрат енергоносіїв:

Wc=(_++)/2,     Gc=(_++)/2.     (8)

Формули (7) i (8) визначають координати центра симетрування - точку С у тривимірному npocтopi (рис.3). Ідея методу, що пропонується, є такою ж самою: через початкову точку Ãn, i точку С провести пряму. Шукана точка Ак знаходиться на відстані АкC = ÃnC. Координати цієї точки визначаються аналогічно (6):

Wк = 2Wc - п ,     Gк = 2Gc - п .    (9)

          Відміна полягає в тому, що початкові дані беруться з масиву точок з п>Vc. Тому початкові координати енергоносіїв не обов'язково будуть більшими за середні значення (9). У зв'язку з цим більші координати (точка Ãn ) будуть зменшуватися, а менші - збільшуватися.
          Стандарт σW, σG обчислюються по об’єднаних масивах координат п, Wк i п, Gк. 3а аналогією з (5) границі діапазонів стаціонарних коливань становлять:

Wmax,min=<Wc±βσW,      Gmax,min=<Gc±βσG          (10)

Викиди параметрів за верхні границі є перевитратами енергоносіїв. Провали за нижні границі можуть розглядатися як енергозбереження, якщо їм відповідають об'єми випуску продукції в допустимому діапазоні (5). Якщо ж є недовідпуск продукції, то зменшення витрат енергоносіїв очевидно не визначає енергозбереження.
          При кількості n > 3 енергоносіїв або інших параметрів (наприклад, параметрів електромагнітної сумісності) симетрування виконується аналогічно, але в n-мірному просторі.


Рисунок 3

Заключні зауваження.

     1. До цього припускалося, що необмеженість ординат нормального розподілу не заважає його застосуванню: стандарт настільки малий у порівнянні зі середнім значенням, шо функція розподілу практично знаходиться в діапазоні робочих значень пapaмeтpiв режиму. Окрім того, не враховувалися обмеження щодо максимуму продуктивності, перевищення якого веде до швидкого зносу устаткування. У цих випадках симетрування виконується аналогічно, але у якості теоретичного вибирається усічений нормальний розподіл [2].
    2. Гіпотеза щодо нормального розподілу випуску продукції i витрат енергоносіїв витікає з физики задачі. Для питомих витрат енергоносіїв

ρ = W / V , g = G / V

          вона не може бути прийнятою, оскільки функція ділення є нелінійною. З цієї причини межі допустимих змін питомих витрат некоректно визначати по границях випуску продукції i витрат енергоносіїв - для цього потрібно знайти імовірні розподіли відношень двох нормальних величин i по них з імовірностями 0,05 i 0,95 визначити цi границі.
    3. За недовідпуском продукції i перевитратам екергоносіїв оцінюються збитки від порушення раціонального режиму. Окрім того, ці показники дозволяють на ранній стадії знайти погіршення стану технологічного устаткування, тобто їx можна розглядати як непрямі діагностичні ознаки. Якщо перевитрати енергоносіїв починають зростати, то за графіком інтегралу від перевитрат прогнозується вихід з ладу устаткування. Практика показує, що графік інтегралу добре апроксимується параболою, для визначення якої достатньо мати тільки три точки режиму.

Висновки

    1. Визначальною ознакою стаціонарності режиму є симетричність імовірнісних розподілів ординат процесів випуску продукції i витрат енергоносіїв.
    2. Стаціонарну компоненту доцільнот виділяти шляхом симетричного відображення масиву опитних значень o6'eмів випуску продукції на область малих об'емів з наступним симетруванням масивів витрат енергоносіїв.
    3. Математична модель стаціонарного режиму у вигляді системи корельованих нормальних випадкових npoцeciв зміни параметрів режиму дозволяє встановити дiaпaзoннi норми випуску продукції i енергоспоживання, а також недовипуск продукції i перевитрати енергоносіїв.

Література

    1. Брусенцов Л. В. Вычисление осредненого цикла случайного процесса. – Изв. вузов. электромеханика, 1972, № 11. – С.1256-1258.
    2.
    2. Шидловский А.К., Куренный Э.Г. Введение в статистическую динамику систем электроснабжения. – Киев: Наукова думка, 1984. – 271 с.
    3. Свешников А. А. Прикладные методы теории случайных функций. – М.: Наука, 1986. – 463 с.

К библиотеки