|
УДК 621.3.003
КОРЕКЦІЯ НЕЗАКОНОМІРНИХ ВІДХИЛЕНЬ ВІД СТАЦІОНАРНОГО РЕЖИМУ СПОЖИВАННЯ ЕНЕРГОНОСІЇВ
Лютий О.П.
ВАТ «Дніпроспецсталь»
Дмитрієва О.М.
Донецкий державний технічний університет
Наукові праці ДонНТУ - Електротехніка і енергетика - 2004 - випуск 79
Annotation - Тhе task of extraction of stationary component of process
of mode parameters is considered. The methods of correction of graphics
of productions ceiling and consumption of power carriers proposed.
The range norms of mode parameters are determined.
Key words – consumption of power carriers, productions ceiling,
stationary mode, correction, range norms.
ПОСТАНОВКА ЗАДАЧІ
Задачі аналізу
і керування процесами споживання енергоносіїв (електроенергії W, газу G, тощо)
на підприємствах повинні вирішуватися у рамках математичних моделей, які відповідають режиму
стабільної продуктивності. Умовою стаціонарності процесів випуску продукції V
і енергоспоживання є незалежність їх характеристик (середніх значень, дисперсій та інш.) від часу t.
Внаслідок випадкових факторів пара¬метри режиму коливаються навколо своїх середніх значень Vс,
Wс, Gс. Ці коливання слід вважати законо¬мірними, якщо вони не порушують
стаціонарність.
На діючих підприємствах є і незакономірні коливання, які зумовлено затримками і порушеннями технологічного
процесу. Для оцінювання недовипуску продукції і перевитрат енергоносіїв з експериментальних графіків
зміни за часом параметрів режиму потрібно виділити їх стаціонарні компоненти й на основі стаціонарної
моделі виконати корекцію графіків і встановити допустимі діапазони зміни параметрів.
Задача корекції записаного графіка  (t)
випуску продукції є вирішеною: в [1] наведено якісне обґрунтування методу симетрування, а в [2,3] – його
кількісну реалізацію. Цей метод з деяким уточненням прийнято і далі. Проте його розповсюдження
на споживання енергоносіїв зустрічає принципову трудність, зумовлену тим, що процеси енергоспоживання
залежать від (t)
випуску продукції є вирішеною: в [1] наведено якісне обґрунтування методу симетрування, а в [2,3] – його
кількісну реалізацію. Цей метод з деяким уточненням прийнято і далі. Проте його розповсюдження
на споживання енергоносіїв зустрічає принципову трудність, зумовлену тим, що процеси енергоспоживання
залежать від  (t), а тому їх не
можна розглядати окремо. Так, зниження витрат електроенергії не завжди є економією,
бо воно може бути викликане недовипуском продукції. (t), а тому їх не
можна розглядати окремо. Так, зниження витрат електроенергії не завжди є економією,
бо воно може бути викликане недовипуском продукції.
Подолання цієї труднощі може бути здійснено різними шляхами:
наприклад, у [3] запропоновано ви¬конувати симетрування у тривимірному просторі
 , ,  , ,  за умови, що центр симетрування визначається по половинах значень трьох процесів, а зберігаються
лише значення з великими абсцисами
за умови, що центр симетрування визначається по половинах значень трьох процесів, а зберігаються
лише значення з великими абсцисами  . Однак
такий підхід не гарантує відтворення залежностей питомих витрат енергоносіїв від випуску продукції.
Метою статті є розробка методу корекції, який базується саме на таких залежностях. . Однак
такий підхід не гарантує відтворення залежностей питомих витрат енергоносіїв від випуску продукції.
Метою статті є розробка методу корекції, який базується саме на таких залежностях.
КОРЕКЦІЯ ПРОЦЕСУ ВИПУСКУ ПРОДУКЦІЇ
Початковими для
корекції є графіки зміни за часом параметрів режиму. За змістом вони визначають¬ся за
час технологічної операції, зміну, добу, місяць. Чим більше час, тим меншим є
діапазон закономірних відхилень.
Для визначеності виклад
будемо вести на при¬кладі однієї вугільної шахти. Добові значення випуску
продукції, спожитої електроенергії і питомих витрат  за один місяці 2005 р. з N=30 днями приведено в табл. 1 (стовпці 3-5), в якій для
подальшого аналізу значення
за один місяці 2005 р. з N=30 днями приведено в табл. 1 (стовпці 3-5), в якій для
подальшого аналізу значення  (t) розташовано у
порядку зростання: номер i=1,2,…,N. Параметри режими вимірюються у системі
відносних одиниць (в.о.), в якій за одиниці прийнято найбільші значення величин (t) розташовано у
порядку зростання: номер i=1,2,…,N. Параметри режими вимірюються у системі
відносних одиниць (в.о.), в якій за одиниці прийнято найбільші значення величин  i
i  . Статистичні середні значення і стандарти становлять: . Статистичні середні значення і стандарти становлять:
 с=0,731, с=0,731,  с=0,955, с=0,955,
 V=0,177, V=0,177,  W=0,03. W=0,03.
Таблиця 1
Номер
i |
Дні |
 |
 |
 |
 |
F |
ρ |
W |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 1 |
30 |
0,2941 |
0,8634 |
2,9356 |
0,5600 |
0,0333 |
1,6944 |
0,9489 |
| 2 |
28 |
04164 |
0,9459 |
2,2715 |
0,5956 |
0,0667 |
1,5960 |
0,9507 |
| 3 |
21 |
0,5139 |
0,9485 |
1,8455 |
0,5972 |
0,1000 |
1,5920 |
0,9507 |
| 4 |
24 |
0,5139 |
0,9433 |
1,8355 |
0,6126 |
0,1333 |
1,5530 |
0,9514 |
| 5 |
23 |
0,5604 |
0,9356 |
1,6695 |
0,6157 |
0,1667 |
1,5455 |
0,9516 |
| 6 |
17 |
0,5619 |
0,9536 |
1,6971 |
0,6405 |
0,2000 |
1,4876 |
0,9528 |
| 7 |
18 |
0,6037 |
0,9948 |
1,6479 |
0,6560 |
0,23333 |
1,4536 |
0,9535 |
| 8 |
26 |
0,6192 |
0,9485 |
1,5318 |
,6916 |
0,2667 |
1,3813 |
0,9552 |
| 9 |
1 |
0,6238 |
0,9253 |
1,4832 |
0,7117 |
0,3000 |
1,3436 |
0,9562 |
| 10 |
12 |
0,6533 |
0,9433 |
1,4440 |
0,7163 |
0,333 |
1,3352 |
0,9564 |
| 11 |
25 |
0,6533 |
0,9588 |
1,4677 |
0,7535 |
0,3667 |
1,2717 |
0,9582 |
| 12 |
2 |
0,6672 |
0,9407 |
1,4100 |
0,7550 |
0,4000 |
1,2692 |
0,9583 |
| 13 |
4 |
0,6811 |
0,9691 |
1,4228 |
0,7643 |
0,4333 |
1,2544 |
0,9588 |
| 14 |
7 |
0,6827 |
0,8840 |
1,2950 |
0,7674 |
0,4667 |
1,2495 |
0,9589 |
| 15 |
11 |
0,7059 |
0,9871 |
1,3984 |
0,7800 |
0,5000 |
1,2302 |
0,9595 |
| 16 |
3 |
0,7864 |
0,9716 |
1,2356 |
0,7864 |
0,5333 |
1,2206 |
0,9598 |
| 17 |
10 |
0,7926 |
0,9768 |
1,2325 |
0,7926 |
0,5667 |
1,2114 |
0,9601 |
| 18 |
27 |
0,7957 |
1,0000 |
1,2568 |
0,7957 |
0,6000 |
1,2069 |
0,9603 |
| 19 |
16 |
0,8050 |
0,9562 |
1,1879 |
0,8050 |
0,6333 |
1,1935 |
0,9607 |
| 20 |
8 |
0,8065 |
0,9562 |
1,1856 |
0,8065 |
0,667 |
1,1913 |
0,9608 |
| 21 |
20 |
0,8437 |
0,9536 |
1,1303 |
0,8437 |
0,7000 |
1,1410 |
0,9626 |
| 22 |
19 |
0,8483 |
0,9897 |
1,1667 |
0,8483 |
0,7333 |
1,1350 |
0,9628 |
| 23 |
22 |
0,8684 |
0,9227 |
1,0625 |
0,8684 |
0,7667 |
1,1098 |
0,9638 |
| 24 |
9 |
0,9040 |
0,9665 |
1,0691 |
0,9040 |
0,8000 |
1,0680 |
0,9655 |
| 25 |
29 |
0,9195 |
0,9639 |
1,0483 |
0,9195 |
0,8333 |
1,0509 |
0,9663 |
| 26 |
6 |
0,9443 |
0,9716 |
1,0290 |
0,9443 |
0,8667 |
1,0246 |
0,9675 |
| 27 |
15 |
0,9474 |
0,9974 |
1,0528 |
0,9474 |
0,9000 |
1,0214 |
0,9676 |
| 28 |
13 |
0,9628 |
0,9588 |
0,9958 |
0,9628 |
0,9333 |
1,0058 |
0,9684 |
| 29 |
5 |
0,9644 |
0,9639 |
0,9995 |
0,9644 |
0,9667 |
1,0042 |
0,9685 |
| 30 |
14 |
1,0000 |
0,9510 |
0,9510 |
1,0000 |
1,0000 |
0,9702 |
0,9702 |
Першим кроком до корекції є
визначення статистичної функції розподілу F(  )=i / N,
яку представлено на рис. 1 графіком 1. Згідно [2] симетрування потрібно виконувати відносно точки М перетину горизонталі 0,5 з графіком функції розподілу.
Абсциса точки М є середнім значенням Vс гіпотетичної моделі стаціонарного режиму. )=i / N,
яку представлено на рис. 1 графіком 1. Згідно [2] симетрування потрібно виконувати відносно точки М перетину горизонталі 0,5 з графіком функції розподілу.
Абсциса точки М є середнім значенням Vс гіпотетичної моделі стаціонарного режиму.

Рисунок 1 — Симетрування статистичної функції розподілу випуску продукції
Оскільки графік статистичної функції розподілу по суті є
східчастим, потрібно розглядати два випадки. Коли кількість днів є непарною, горизонталь 0.5 попадає на
вертикальний стрибок при абсцисі  (N+1)/2,
яку і потрібно приймати за середнє значення. Якщо кількість днів є парною, то
горизонталь 0,5 попадає на горизонтальну ділянку між абсцисами (N+1)/2,
яку і потрібно приймати за середнє значення. Якщо кількість днів є парною, то
горизонталь 0,5 попадає на горизонтальну ділянку між абсцисами  N/2 i N/2 i
 N/2+1. N/2+1.
У [2] запропоновано приймати середнє значення
Vc = (1/2) • (  N/2 + N/2 +  N/2+1), (1) N/2+1), (1)
але при великій різниці між доданками в (1) воно мо¬же бути декілька заниженим. У такому випадку сере¬днє значення доцільно знаходити по
точці перетину з горизонталлю 0,5 прямої, яка проходить через дві наступні після F( N/2)
ординати. Можна показати, що абсциса цієї точки становить N/2)
ординати. Можна показати, що абсциса цієї точки становить
Vc = 2  N/2+1 + N/2+1 +  N/2+2 , (2) N/2+2 , (2)
Таким чином, при парній кількості днів потрібно брати найбільше зі значень (1) або (2). У прикладі,
що розглядається, на рівні 0,5 є горизонтальний відрізок з кінцевими абсцисами  15=0,7059 i 15=0,7059 i
 16=0,7864, а наступна абсциса 16=0,7864, а наступна абсциса  17=0.7926.
Формули (1) і (2) дають значення 0,746 i 0,78, тому приймаємо Vc = 0.78. Яке є більшим ніж статистичне значення 0,731,
що свідчить про наявність незакономірних зменшень випуску продукції. 17=0.7926.
Формули (1) і (2) дають значення 0,746 i 0,78, тому приймаємо Vc = 0.78. Яке є більшим ніж статистичне значення 0,731,
що свідчить про наявність незакономірних зменшень випуску продукції.
Значення  випуску продукції, більші за
Vc, зберігаються. Для повноти заповнення табл. 1 вони зі стовпця 3 переносяться в стовпець 6
(номери з 17 до 30). При i=N/2=16 замість експериментального значення 0,7864 потрібно записати середнє значення 0,78. Якщо кількість днів непарна, то середнє значен¬ня в стовпець 6 не вноситься. випуску продукції, більші за
Vc, зберігаються. Для повноти заповнення табл. 1 вони зі стовпця 3 переносяться в стовпець 6
(номери з 17 до 30). При i=N/2=16 замість експериментального значення 0,7864 потрібно записати середнє значення 0,78. Якщо кількість днів непарна, то середнє значен¬ня в стовпець 6 не вноситься.
Малі значення випуску продукції коректуються за формулою
 i = 2Vc - i = 2Vc -  N - i+1, (3), N - i+1, (3),
яка забезпечує центральну симетрію відносно точки М функції розподілу F( )
скоректованих значень (графік 2 на рис. 1). В області значень абсцис, більших за Vc, графіки 1 і 2 співпадають. )
скоректованих значень (графік 2 на рис. 1). В області значень абсцис, більших за Vc, графіки 1 і 2 співпадають.
По симетрованому масиві розраховується стандарт випуску продукції у стаціонарному режимі
 , (4) , (4)
У силу симетрії імовірного розподілу
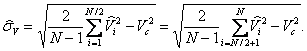 , (5) , (5)
Розрахований стандарт приймається за стандарт σV
теоретичної моделі. Оскільки симетрування змен¬шує діапазони зміни випуску продукції, цей стандарт є меншим за
стандарт  V експериментальних значень:
у прикладі, що розглядається. - 0,124 проти 0.19. V експериментальних значень:
у прикладі, що розглядається. - 0,124 проти 0.19.
Закономірні коливання режиму зчиняються під дією
великої кількості факторів, тому розподіл випуску продукції природно прийняти нормальним з параметрами
Vс i σV. При V*=(V-Vс)/σV
його функція розподілу
Fн(V)= Ф*(V*) , (6)
визначається через функцію Ф*(x) стандартного нормального розподілу (крива 3 на рис. 1).
Корекція графіка  (t)
виконується по нижній половині стовпця 6 шляхом заміни (t)
виконується по нижній половині стовпця 6 шляхом заміни  на на  . .
На рис. 2 тонкими лініями показано початковий графік, а стовщеними – скоректований. Малі значення
випуску продукції коректуються у сторону збільшен¬ня, а великі – зберігаються.
Корекцію можна виконати і по теоретичному розподілу F(V)
за умови її рівності статистичній функції розподілу (стовпець 7 табл. 1)
F(V)=F( t)=i/N , (7) t)=i/N , (7)
За номером i скоректоване значення
Vi=arc{F(Vi)}. (8)
У цьому випадку коректуються усі абсциси: як малі, так і великі.
Нормальний закон безпосередньо не можна використовувати для корекції, а потрібно переходити до
зрізаного нормального закону [2] у межах скоректованих значень.
Максимальне і мінімальне розрахункові значення випуску продукції
Vmax,min = Vc±βV σV, (9)
де βV – статистичний коефіцієнт. Вважаючи, що при досягненні найбільшого випуску продукції  M
технічні умови не порушуються, це значення природно приймати за Vmax, що дозволяє знайти статистичний коефіцієнт M
технічні умови не порушуються, це значення природно приймати за Vmax, що дозволяє знайти статистичний коефіцієнт
βV=( M – Vc)/σV. (10) M – Vc)/σV. (10)
У прикладі найбільше значення становить одиниці, тому згідно (10)
βV=1,8, що відповідає граничній імовірності 0.036 (за відсутності даних імовірність приймають
рівною 0,05. а β = 1,65).
Розрахункові значення (9), які дорівнюють 1 і 0,56,
являють собою діапазонні норми випуску продукції (горизонталі 1 і 2 на рис. 2). Затушовані ділянки графіка,
нижчі за горизонталь 2, є недовипуском продукції внаслідок незакономірних відхилень від стаціонарного режиму.

Рисунок 2 — Експерементальний і скоректований графіки випуску продукції
ПИТОМІ ВИТРАТИ ЕНЕРГОНОСІЇВ
Ідея методу, що пропонується, полягає в тому, що
корекція фафіків витрат енергоносіїв здійснюєть¬ся по скоректованому графіку випуску продукції з
використанням залежностей питомих витрат від V. Ці залежності потрібно встановлювати
експериментальним шляхом або за технологічними даними.
За смислом зі зростанням випуску продукції
зростає і енергоспоживання. Якщо статистичну обробку масивів  і
і  виконати формально, то можна отримати
формули взаємозв'язку між ними будь-якого виду. Доцільніше вибрати вид залежності, виходячи з фізики задачі. виконати формально, то можна отримати
формули взаємозв'язку між ними будь-якого виду. Доцільніше вибрати вид залежності, виходячи з фізики задачі.
Так, якісні міркування щодо вибору нормального розподілу
випуску продукції у стаціонарному режимі є справедливими і для енергоспоживання. Випуск продукції і витрати
електроенергії одночасно можуть бути нормальними, якщо вони зв’язані лінійною залежністю
W = aWV + bW , (11)
з постійними коефіцієнтами aW і bW. Тоді питомі витрати
ρ = W / V = aW +bW/ V. (12)
Якщо експериментальні значення питомих витрат не апроксимуються
функцією (12), то необхідно проаналізувати причини розбіжностей. У першу чергу потрібно вилучити з розгляду надто
великі відхилен¬ня: наприклад, коли підприємство ЗУПИНЯЛОСЯ, ТО хоча V = 0, але є постійна складова
витрат електроенергії, а тому питомі витрати стають нескінченими. Ясно, що такі витрати при статистичній обробці не
треба враховувати. Згідно з відомим правилом трьох сигм можна вилучити усі абсциси, меньші за граничне значення
Vx = Vc - 3σV.
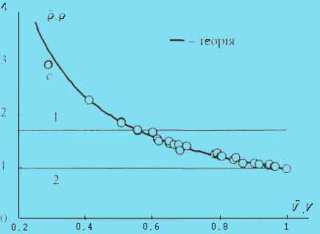
Рисунок 3 — Питомі витрати електроенергії |
|
У прикладі, що розглядається, це значення становить 0.408,
тому перше значення у стовпці 5 враховувати не будемо (точка с на рис. 3). Решта точок добре апроксимується
функцією (12) з коефіцієнтами aW=0,0485 i bW=0,9217 (безперервна крива на рис. 3).
Слід відзначити, що і точка с, яку вилучено, є близькою до теоретичної кривої.
У практиці можливі випадки, коли залежність витрат
електроенергії від випуску продукції не є лінійною, навіть при вилученні даних, що випадають.
У цих випадках приймається фактична залежність.
|
З врахуванням (9) і (12) діапазонні норми питомих витрат
електроенергії становлять
ρmin = aW + bW / Vmax ,
ρmax = aW + bW / Vmin. (13)
У прикладі маємо: ρmin = 0.97 і ρmax = 1,69
(горизонталі 1 і 2 на рис. 3). Перевищення норм спостеріга¬ється для 5 діб – як і на рис. 2.
Аналогічним чином визначаються питомі витрати інших енергоносіїв.
ВИСНОВКИ
1. З фізичних міркувань імовірнісний розподіл
стаціонарної компоненти випуску продукції можна
вважати нормальним. Його характеристики доцільно
знаходити по симетрованій статистичній функції розподілу: шляхом симетричного відображення великих
експериментальних значень об'єму випуску продукції
на область малих значень.
2. Стаціонарні компоненти витрат енергоносіїв
рекомендується розраховувати по стаціонарній компоненті випуску продукції і залежностям питомих
витрат від випуску продукції
3. Діапазонні норми параметрів режиму дозволяють оцінити недовипуск продукції і перевитрати
енергоносіїв.
Література
1. Брусенцов Л. В. «Вычисление осредненого цикла случайного процесса.» – Изв. вузов. электромеханика, 1972, № 11. – С.1256 –1258.
2.
Шидловский А.К., Куренный Э.Г. «Введение в статистическую динамику систем электроснабжения.» – Киев: Наукова думка, 1984. – 271 с.
3.
О.М. Дмитрієва, О.П. Лютий «Метод симетрування для виділення стаціонарних компонент режимів виробництва і витрат енергоносіїв.» – Наукові праці ДонНТУ, серія "Електротехніка і енергетика", випуск 79, Д., 2004. - стр. 100-103.
|