238

1

Abstract—  This  paper  focuses  on  some  important  problems  occurring in designing transformers for static electronic  converters, in low and middle power applications (from few kVA

up to 10-20 MVA); some possible solutions are suggested.

Index  Terms—  Design  of  transformers  for  static  electronic  converters, transformer losses, operation of transformers in non  sinusoidal conditions. 

I.   INTRODUCTION

HE manufacture of transformers used for AC/DC

conversion in high power plants (for example, electrolysis  plants,  with  power  up  to  50  MVA  or  greater)  is  well- established, so the related problems are known and solved in

the design stage. 

Nowadays,   the   growing   spreading   of   static   electronic

converters in many low and middle power applications (from  few kVA up to 10-20 MVA) is forcing transformer

manufacturers  to  take  into  account  some  important  design  features, previously neglected.

This paper focuses on some important problems present in  the cited applications, and suggests some possible solutions. 

II.   SOME SIGNIFICANT CONFIGURATIONS 

To the aim of a right dimension procedure of a transformer,

it is important to know the system in which it works; for this  reason, some examples of conversion systems which need to

be examined with particular care are shown in the following  figures.

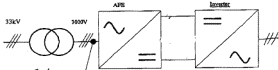
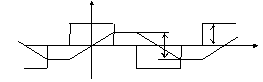
Fig. 1.a shows the scheme of a power supply, in particular  an impressed voltage source 3 level AC/AC static converter,  and Fig. 1.b reports the typical line to line voltage seen from

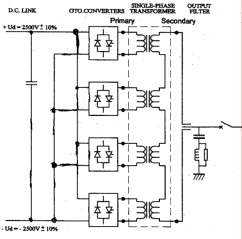
the secondary winding of the input transformer.  

Fig. 2 shows the scheme of a single phase transformer for a

static frequency converter, used for railway vehicle. 

Fig. 3 shows a typical scheme for a three phase transformer

used in a multilevel inverter: on each column one primary and  six secondaries are wound.

Manuscript received June 30, 2006.  

M.Ubaldini   and   G.M.   Foglia   are   with   the   Department   of   Electrical

Engineering, Faculty of Industrial Processes, of Politecnico di Milano, Piazza  Leonardo da Vinci 32, 20133 Milano, Italy; phone: (+39) 02 2399-[3795,3746] 

fax: (+39) 02 23993703; e-mails: [mario.ubaldini, gianmaria.foglia]@polimi.it. 

Fig. 1: a (upper): scheme of an impressed voltage source 3 level AC/AC static  converter;  b  (lower):  typical  line  to  line  voltage  seen  from  the  secondary

winding of the input transformer.

Fig. 2: scheme of a single phase transformer for a static frequency converter,  used for railway vehicle.

III.   MAIN DESIGN PROBLEMS 

The   manufacturers   of   transformers   intended   for   static

energy conversion need to care of some issues, that may bring  to  design  choices which differ deeply from those adopted  in

traditional machines. 

In  particular,  two  types  of  problems  are  very  significant:

one  concerns  the  losses  evaluation  (in  the  magnetic  circuit,  and in the windings), in case of voltages and currents highly

distorted; the other concerns the electromagnetic design of the  machine, which is related to the requirements of the connected

converter.

Design and Reviewing Features in Transformers  used for Power Electronic Converters

Mario Ubaldini, GianMaria Foglia

T


238
2
V1
W1
U2
V2
W2
U3
V3
W3
U4
V4
W4
U5
V5
W5
U6
V6
W6
U
W
U1
V
PRIMARY
SECONDARIES
Fig.  3:  a  typical  scheme  for  a  three  phase  transformer  used  in  a  multilevel  inverter: on each column one primary and six secondaries are wound.
As regards the losses, for a correct transformer design, the   user is requested to provide the manufacturer with some data,  deriving   from   the   analysis   of   the   system   in   which   the
transformer works. Along with the rated values of the machine  quantities  (power,  voltages,  currents,  frequency),  the  main
required data are the following:  - kth order current harmonic amplitude, Ik;    - kth order voltage harmonic amplitude, Vk.
Often,  the  user  fixes  to  the  manufacturer  some  particular  quantities,  for  example  the  maximum  value  of  iron  and/or  winding losses.
Such problems are all present in the schemes of fig. 1, 2, 3.
IV.   JOULE LOSSES IN THE WINDINGS  The evaluation of these losses is similar for all conversion
systems, and does not imply particular difficulties.  Known the current harmonic content (amplitude Ik of the kht
harmonic,  for  all  the  harmonics),  a  finite  element  (FEM)  software is needed to evaluate the additional resistance Radk of
the winding, at the frequency fk .  The  procedure  is  as  follows.  Called  RDC  the  resistance  in
DC, and defined the RMS current value   IRMS = v(Ók Ik2) , 
(1)
the losses in non sinusoidal conditions are  Pns = Ók(RDC + Radk)Ik
2
= RDC ÓkIk
2
+ Ók Radk Ik
2
= PDC + Pad, (2)  where PDC and Pad are DC and additional losses respectively.
V.   IRON LOSSES IN NON SINUSOIDAL CONDITIONS  Let   we   consider   a   transformer   operating   in   no   load
conditions, supplied by a periodic non sinusoidal voltage v(t),  with period T, frequency f = 1/ T, with null average value and
with odd harmonics only. We also assume that during the half  period T/2 the voltage does not reverse (it can be zero, as it
occurs in inverters).  Called Vk  the RMS value of the kht voltage harmonic, the
voltage v(t) can be expressed as Fourier series:  v(t) = Σk v2 V
k
sin(k ù t + ák)       k = 1,3,5,7
....
(3)
The RMS value VRMS of the supplying voltage v(t) is  VRMS = v(Ók Vk2),
(4)
and the average value  Vm of a positive half wave of v(t) is  Vm =(∫T ABSv(t) dt)/T, 
(5)
where ABSv(t) is the absolute value of v(t).  Called ϕc the winding flux linkages, since the voltage v(t)
has a null average value, in steady state the flux varies from  the peak negative value -Öc up to the peak positive value Öc,
without   asymmetrical   hysteresis   loops.   Since   the   voltage  average value can be related to the flux linkages peak value
Vm = 4f Öc , 
(6)
the peak value Öc can be expressed as  Ö
c
= N Afe B = Vm /(4 f ) , 
(7)  where N is the turn number, Afe [m2] is the net section of the  iron core and B [T] the working flux density (peak value).
Called Mfe the iron core mass, the losses can be evaluated.  A.   Hysteresis losses Phy
The same expression of sinusoidal conditions is used:  Phy = Mfe P’hy = Mfe k’i f Bn = ki f Bn ,
(8)  where  P’hy  are  the  losses  per  unit  mass  [W/kg],  k’i  is  a  coefficient (characteristic of the material), n is the Steinmetz
coefficient, equal to 1.5-2.0 for flux density B = 1.0-2.0 T.  Such  expression  is  used,  because  the  hysteresis  losses
depend just on the area of the hysteresis cycle and on the time  interval needed to cover it (equal to the period T = 1/f of the
supplying  voltage/current), so they are  equal to  the losses in  sinusoidal conditions, with the same frequency f and working
flux density B. In other words, the voltage harmonics do not  affect the hysteresis losses, except calling for a working flux
density lower than the value used in sinusoidal conditions.

238
3
B.   Eddy current losses Ped  Unlike  the  hysteresis  losses,  the  eddy  current  ones  are
greatly  dependent  on  the  harmonic  content  of  the  supply  voltage, as we can see from the expression of the RMS value
Vk of the kth harmonic,    Vk = 4.44 N k f Afe Bk ,  
(9)  where N is the turn number, Afe is the area of the core, Bk is  the peak value of the kth harmonic of the flux density. So 
k f Bk = Vk /(4.44 N Afe) = â Vk           â = 1/(4.44 N Afe)   (10)
The eddy current losses Pedk  of the kth harmonic are  Pedk = Mfe  k’c (k f Bk)2
= kc Vk2            kc = Mfe  k’c  â2  
(11)  where  k’c  is  a  coefficient  dependent  on  the  material  and  the  geometric dimension of the laminations. For the fundamental
harmonic (k = 1), the hysteresis losses are  Ped1 = kc (V1)2 . 
(12)  Note  that  the  flux  density  B1  related  to  the  fundamental
voltage V1 is different from the working flux density B in (7).  The total eddy current losses Pedt  are:
Pedt = Ók Pedk = Ó
k
kc (Vk)2 =
Ped1(Ó
k
Vk2 ) / V12  =
Ped1 (VRMS / V1)2 . 
(13)
VI.   IRON LOSSES IN MOST SIGNIFICANT CONDITIONS  Let we know the material losses characteristics, for
sinusoidal conditions at different frequencies.     A.   The waveform of the voltage v(t) is known.
In  this  case,  the  average  value  Vm    of  the  voltage  v(t)  is  calculable, and so the working flux density B (peak value) can      be chosen by (7). From the fundamental RMS value 
V1 = 4.44 N f Afe B1 , 
(14) 
the related fundamental flux density B1 is gained.  If  it  is  possible  to  separate  the  specific  hysteresis  losses
from the eddy current ones, the expressions (7) and (13) can     be  applied.  Otherwise,  some  designers  divide  in  two  equal
parts the specific losses, and operate again with (7) and (13);     other  designers,  evaluate  the  total  specific  iron  losses  P’fe  at
working   flux   density   B   and   frequency   f,   in   sinusoidal  conditions, and they calculate the iron losses in non-sinusoidal
condition with the following expression:  Pfe= Mfe P’fe (VRMS / V1)2 . 
(15)  Such expression is meaningful when the frequency is high
(greater  than  1  kHz),  because  in  this  case  the  eddy  current  losses are much greater than the hysteresis ones.
In  the  following,  two  evaluation  examples  are  shown,  supposing  to  supply  the  transformer  by  a  square  wave  VSI  inverter, with a voltage conduction period of ð or 2ð/3.
1)   Conduction period of ð.  Fig. 4 shows the waveforms of the supply voltage v(t) and
of the linkage flux ϕc(t) (with peak value Öc = N
Afe B). 
v(t)
ϕc(t)
V
Öc
ùt
Fig. 4: waveform of the linkage flux ϕc(t) when the supply voltage v(t) is a  square wave, with a conduction period of ð.
The following results hold:      average value: Vm = V = 4 f Öc = 4 f N
Afe B
RMS value: VRMS = V   fundamental RMS value: 
V1 = 2 v2 V/ð = 0.900 V = ðv2 f N
Afe B1 = 4.44 f N
Afe B1
ratio B/B1 = ð2 / 8 = 1.234  (VRMS  /
V1)2 = (ð / 2v2)2 = 1.234   So,  the  losses  in  non  sinusoidal  condition  are  1.234  times
those in sinusoidal conditions:  Pedt =
Ped1 (VRMS / V
1)2 = 1.234 .  2)   Conduction period of 2ð/3. 
Fig. 5 shows the waveforms of the supply voltage v(t) and  of the linkage flux ϕc(t) (again with peak value Öc= N
Afe B). 
v(t)
ϕc(t)
V
Öc
ùt
Fig. 5: waveform of the linkage flux ϕc(t) when the supply voltage v(t) is a  square wave, with a conduction period of 2ð/3.
The following results hold:  average value: Vm = V (2/3) = 4 f Öc = 4 f N
Afe B
RMS value: VRMS = V v(2/3) = 0.816 V  fundamental RMS value: 
V1 = v6 V/ð = 0.780V = ðv2 f N
AfeB1 = 4.44 f N
AfeB1
ratio B/B1 = ð2 / (6v3) = 0.950  (VRMS  /
V1)2 = (ð / 3)2 = 1.097   So, the losses in non sinusoidal condition are 1.0.97 times
those in sinusoidal conditions:  Pedt =  Ped1 (VRMS / V
1)2 = 1.097 .  B.   The waveform of the voltage v(t) is not known, but the  harmonic contents is defined.
This  is  a  quite  usual  situation:  the  transformer  purchaser  together   with   the   rated   value   of   the   quantities   (voltage,  current,  frequency)  requires  also  the  RMS  value  Vk  of  the
most   important   harmonics.   Since   the   phases   ák   of   the  harmonics  are  not  known,  the  average  value  Vm  can’t  be
evaluated; as a consequence, the flux density working value B  can  be  calculated  with  reference  to  an  equivalent  sinusoidal
voltage, whose RMS value is    VRMS = v (Ó
k
Vk2 ), 
(16)
using the common relation   VRMS = 4.44 N f Afe B .  
(17)  In  this  case,  many  designers  evaluate  the  iron  losses  in
sinusoidal   conditions   Pfes   =   Pfe1,   with   reference   to   the  fundamental voltage (RMS value V1, frequency f, flux density
B1),  and then they evaluate the iron losses  in non  sinusoidal  conditions Pfens by the expression:
Pfens = Pfes (VRMS / V
1)2 .  
(18)
Evaluation example.  The supplying voltage of a three phase power transformer has  the following harmonic contents:
k = fk/f
13
19
25
37
47
Vk/Vn
0.04
0.06
0.25
0.12
0.08

238
4
The voltage RMS value is VRMS = 1.043 V1. Calculated the  iron losses Pfes at the fundamental voltage Vn= V1, the losses    in non sinusoidal conditions are
Pfens = Pfes (VRMS / V
1)2 = 1.09 Pfes .
VII.   TRANSFORMER ELECTROMAGNETIC DESIGN  Three   phase   transformers   devoted   to   supply   multilevel
converters  may  have  a  high  number  of  secondary  windings,  from  4  up  to  more  than  20  windings.  To  obtain  the  desired
phase displacement among the secondary voltages, the  secondary windings cannot be equal, but need some additional
shifter windings.  Fig.   3   shows   the   scheme   of   a   transformer   with   six
secondary  windings,  of  “extended  delta”  type:  each  base  secondary winding is delta connected, but one shifter winding
is linked to each side of the delta. With a suitable turn number  of  the  windings  (both  the  base  and  the  shifter  ones),  the
desired phase shift can be obtained, in the no-load operation:  in the example,  the phase shifts obtained  are -25, -15, -5,  5,
15, 25 electrical degrees.   As a matter of fact, the shift in loaded operation can be very
different  from  the  no-load  one;  this  is  due  to  the  different  values of the leakage reactances between the primary and each
of the secondary windings, or between two secondaries each  other,  which  causes  different  reactive  voltage  drops  in  the
phases under commutation. This problem is usually solved in  two ways, which heavily affect the primary winding design.
One way consists in dividing the primary phase windings in      as  many  parts  as  the  number  of  secondary  windings  (all  the  parts  of  the  primary  are  then  connected  in  parallel);  this
solution is used, for example, in 12-phase conversion systems,  with  two  secondaries,  one  delta  connected,  the  other  wye.
Theoretically  it  is  a  simple  idea,  but  for  constructional  and  cost reasons, it is unfeasible with a high number of secondary
windings.  The other way, uses suited control systems which act on the
valves, and advance or delay their conduction, to correct the  phase shifts. This is a cheaper solution (because the primary
phase windings are made just with a single coil), and so it is  the most adopted.
Sometimes, the cited control system  may not be effective:  in  this  case,  a  trade  off  solution  is  adopted,  dividing  the  primary phase windings in two parallel coils.
To give an example of the discussed issue, Table I shows  the  p.u.  short  circuit  voltage  of  the  transformer  of  Fig.  3,  in  both cases of primary phase windings made of one single coil
or two parallel coils: it is clear how the latter solution allows a  significant reduction of the short circuit voltage.
The  previous  values  of  short  circuit  voltages  have  been  obtained solving (by PSpice) suited circuits. We note that due   to  the  high  number  of  windings  (13  for  each  column),  a
network  based  on  the  binary  short  circuit  impedances  is  not  usable.  For  this  reason,  we  calculated  the  self  and  mutual
inductances of all the windings (3·13·12/2 inductances), by a  FEM  software  (Maxwell  2D),  with  a  fixed  value  of the  iron
permeability;  then,  a  suited  three  phase  equivalent  network  has  been  considered  and   solved  for  each  analysed  short
circuit:  for  example,  to  study  the  short  circuit  between  one  primary  and  one  secondary,  the  network  involves  6  coils  (3
primaries  and  3  secondaries),  each  characterised  by  the  own  self   inductance   and   the   related   mutual   inductances,   the
primary is supplied, the secondary is short circuited.
TABLE I: SHORT CIRCUIT VOLTAGE IN THE TRANSFORMER OF
FIG. 3, SUPPOSING THE PRIMARY PHASE WINDINGS MADE OF ONE  SINGLE COIL OR TWO PARALLEL COILS.  
Supplied   winding
Short  circuited 
winding
Single   primary
coil
Two  parallel 
coils
Primary
All 6  secondaries
0.123
0.123
Primary
One  secondary
min
0.101
0.079
Primary
One  secondary
max
0.202
0.126
One  secondary
One  secondary
min
0.159
0.159
One  secondary
One  secondary
max
0.547
0.238
NOTE:  The  “min”  and  “max”  cases  refer  to  the  minimum  and  maximum  voltage  values  obtained  in  all  the  possible  situations:  6  cases  supplying  the
primary and short circuiting one secondary, 15 cases supplying one secondary  and short circuiting another secondary.
REFERENCES
[1] GianMaria  Foglia,  Mario  Ubaldini,  “D.C.  Component  in  Transformer:  Physical  Behavior  and  Design  Features”,  proceedings  of  ICEM’2004,  International  Conference  on  Electrical  Machines,  Krakow,  Poland,  5-8
September 2004.