Cтатья подготовлена для публикации в трудах Всеукраинской научно-технической конференции студентов «Электротехника, электроника и микропроцессорная техника», ДонНТУ, 2008 год
УДК 621.316.9
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ РАЗРЯДОВ РАЗМЫКАНИЯ В ИСКРОБЕЗОПАСНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ ПОСТОЯННОГО ТОКА
Бондаренко Т.А., магистрант; Бершадский И.А., доц., к.т.н.
(Донецкий национальный технический университет, г. Донецк, Украина) Автоматизация производственных процессов на шахтах, опасных по газу и пыли, во взрывоопасных помещениях предприятий химической, нефтяной и газовой промышленности требует повышения безопасности труда, связанного с применением электрической энергии [1]. Одним из наиболее эффективных и экономически оправданных направлений в решении поставленной задачи является широкое применение искробезопасных устройств.
Теоретической основой методов оценки искробезопасности электрических цепей должна стать математическая модель электрического зажигания взрывоопасных газовых смесей, которая учитывает все важнейшие факторы, определяющие исследуемый процесс.
В теории искробезопасности разрабатывались расчетные методы оценки воспламеняющей способности электрических цепей. При этом прибегали к эквивалентированию, то есть замене реальной сложной цепи более простой с равной вероятностью зажигания взрывоопасной газовой смеси, а, следовательно, соблюдалось равенство энергий разрядов, токов и ЭДС источников питания.
В дальнейших исследованиях методика была усовершенствована. Так, введено понятие критического времени нагрева взрывоопасной газовой смеси τкр и два критерия искробезопасности – энергетический при τр≤ τкр и мощностный при τр >>τ кр [2]. Однако и в этом случае не исключены существенные недостатки.
Поэтому основным методом оценки искробезопасности остается экспериментальный, основанный на испытании электрических цепей во взрывных камерах.
Современные исследования установили, что расчетная оценка искробезопасности должна сводиться к определению энергии Wp, мощности Pp и длительности tp электрического разряда, возникающего при известных параметрах цепи и источников. Основным препятствием на пути создания методик для таких расчетов, на наш взгляд, было отсутствие обобщенной модели, связывающей переходный процесс при заданной скорости размыкания контактов, характеристику разряда и его воздействие на процесс образования ядра пламени.
Осциллографирование показало [3], что разряды размыкания в индуктивных цепях имеют длительный характер и, принимая плавный закон убывания тока, характерный для дугового размыкания цепи, учитываем случай наиболее полной реализации магнитной энергии и энергии источника тока. Допустимость принятой модели подтверждается исследованиями [3,4].
Целью исследования является определение параметров разряда в искробезопасной цепи без учета влияния емкостных элементов и дальнейшая проверка опасности в отношении развития ядра пламени, т.е. взрывобезопасности.
Достаточно полно в количественном отношении электрическая дуга может быть описана выражениями баланса энергии в столбе разряда. Для этого используются соотношения динамической характеристики дуги [5].
Необходимые параметры разряда в искробезопасной цепи заданной конфигурации получаем, используя Simulink – модель программного комплекса MatLAB 6.5.
Блок размыкания электрической цепи (рис.1) встраивается в схему, а постоянная времени τ и отводимая мощность автоматически адаптируются к коммутационному процессу. В основу модели положен управляемый по напряжению источник тока (Controlled Current Source). Измерительный блок (Voltage Measurement) и источник тока взаимодействуют, осуществляя связь между электрическими сигналами (напряжением и током, протекающим в разряде) через переходную функцию (блок Simulink DEE).

Рисунок 1 – Блок размыкания электрической цепи
Система уравнений Майра (1) записана с помощью редактора дифференциальных уравнений DEE. В нем приводится символическая запись вида:


где u(1) – первый вход DEE блока, эквивалентный напряжению на дуге u; u(2) – второй вход DEE блока, представляющий логику размыкания цепи: u(2)=0, когда контакт замкнут и u(2)=1, когда контакт начинает дуговое размыкание; u(3) – обратная связь по току разряда для вычисления; u(4) – модельное время t; u(5) – постоянная времени дуги τ; x0 – начальная величина проводимости дуги g(0); x(1) – переменная состояния диффуравнения, ln(g); y – выход блока DEE, равный току дуги i; Pp – отводимая от дуги мощность.
Параметры v, мм/с, g(0), См, сirc br, c определяются пользователем в диалоговом окне. Simulink – блок «Step» используется для управления моментом размыкания цепи: при замкнутом контакте решается ДУ  . В Simulink блок «Hit Crossing» используется для моделирования нелинейного сопротивления дуги при переходе напряжения через ноль, а блок «Step» – для управления моментом размыкания цепи: при замкнутом контакте решается ДУ .
. В Simulink блок «Hit Crossing» используется для моделирования нелинейного сопротивления дуги при переходе напряжения через ноль, а блок «Step» – для управления моментом размыкания цепи: при замкнутом контакте решается ДУ .
Проверка методики, которая оценивает параметры цепи на искробезопасность осуществляется на примере простейшей омической цепи, индуктивной, индуктивной с линейным омическим шунтом. Опасность заданных параметров разряда характеризуется возникновением устойчивого фронта пламени или разрушением очага воспламенения, т.е. изолиниями температуры в пространстве с учетом влияния диаметра электродов и длины межконтактного промежутка на энергию зажигания.
1. Омическая цепь
Oценка искробезопасности проводилась для последовательно установленного источника питания – батареи E=24 В и неповреждаемого резистора R (R1=33 Ом, R2=15,5 Ом) при токах в цепи I01 = 0,73 А, I02 = 1,55 А. C учетом коэффициента запаса 1,5 получили измененную цепь с I01=1,1А, I02=32А. Энергия разряда Wp, и его длительность Tp при размыкании контактов с различными скоростями (от 0,045 м/с до 6,5 м/с) просчитывалась на компьютерной модели, а затем сравнивалась с аналогичными расчетными данными, приведенными в ГОСТ [6].
2. Индуктивная цепь
Исследования проводились для последовательного соединения источника постоянного тока – батареи E=24 B, 70 B и RL – ветви (L=0,01 Гн, 0,1 Гн). Так как расчетные данные в ГОСТ отсутствуют, воспламеняющая способность определялась по характеристикам искробезопасности I-E-L [6]. Предварительно было установлено, что наиболее опасны высокие скорости размыкания (ν=6500 мм/с).
3. Индуктивная цепь c омическим шунтом
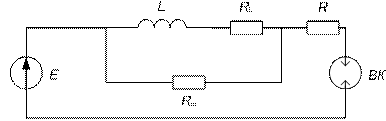
Исследования проводились для данной схемы с напряжением источника питания E=10 B, статической индуктивностью L=0,1 Гн, омическим сопротивлением индуктивного элемента RL=25 Ом, сопротивлением шунта Rш=1000 Ом.
На основе разработанной модели дугового разряда по уравнению Майра с учетом теплофизических свойств столба плазмы показана возможность её использования для расчетной оценки искробезопасности на примере омической и индуктивной цепей. Сравнение результатов расчетов по разработанной методике с известными формулами [6] и характеристиками искробезопасности показывают удовлетворительную сходимость.
ЛИТЕРАТУРА
1. Жданкин В.К. Вид взрывозащиты «искробезопасная электрическая цепь» //Журнал СТА. -1999. - №2.
2. Коган А.Г. Электроизмерительная и расчетная оценка искробезопасности индуктивных электрических цепей на основе математической модели очагового зажигания рудничных газов: Автореф. дис. канд. техн. наук: 05.26.01, Макеевка, 1988.
3. Петренко Б.А. Вопросы теории и расчет искробезопасных электрических цепей // Механизация и автоматизация в горной промышленности: Сборник статей. Вып.2 / ИГД им. А.А. Скочинского. – М.: Госгортехиздат, 1962.
4. Комаров В.С. Искробезопасность рудничного и взрывозащищенного оборудования. М.: Недра, 1972.
5. P.H. Schavemaker and L. Van der Sluis . The arc model blockset//Proceedings of the Second IASTED International Conference POWER and energy systems (EuroPES) June 25-28, 2002, Crete, Greece. pp. 644-648.
6. ГОСТ P 51330.10 – 99 (МЭК 60079 – 11 – 99). Электрооборудование взрывозащищенное, ч.11 – Искробезопасная электрическая цепь. Госстандарт России от 09.12.1999 г. – М.: Изд-во стандартов, 1999.