К ОПРЕДЕЛЕНИЮ ЭКВИВАЛЕНТНОГО ТОКА И КОЛИЧЕСТВА ПОГЛОЩЕННОЙ ЭНЕРГИИ ТЕЛОМ ЧЕЛОВЕКА, ПОПАвшего ПОД НАПРЯЖЕНИЕ СЕТИ с изолированной нейтралью

 Назад

Чорноус Е.В., Ковалев А.П., Чорноус В.П.

Донецкий национальный технический университет

emitoe@yandex.ru

К интегральным показателям, характеризующим степень опасности сети относится эквивалентный ток через тело человека, оказавшегося под фазным напряжением, и количество поглощенной им электромагнитной энергии. Их достоинство заключается в комплексном учете различных факторов (несколько этапов аварийной ситуации с переходными процессами на их границах, работа устройства компенсации, выбег двигателей после защитного отключения сети и др.). Применительно к шахтным низковольтным сетям (U = 660 или 1140 В, нейтраль изолирована, нагрузка – асинхронные электродвигатели мощностью от 100 до 250 кВт) по методике расчета интегральных показателей накоплен определенный опыт [1, 2]. Тем не менее, существует ряд параметров, строгий учет которых затрудняется влиянием случайных факторов или недостатком информации. К ним относятся, прежде всего, электромагнитная Т_Э и механическая Т_М постоянные времени двигателей в режиме выбега. Кроме того, влияние работы компенсирующих устройств в этом режиме также недостаточно исследовано.

Согласно [3] значение постоянной времени Т_Э в зависимости от мощности и количества параллельно работающих двигателей находится в пределах 1.0…1.5 с. Что же касается механической постоянной Т_М, определяющей время замедления двигателя, то она может находится в более широких пределах от 0.5 до 5…8 с.

Задача данного исследования: оценить влияние на интегральные показатели постоянных времени Т_Э и Т_М, а также определение режима компенсации на этапе свободного выбега двигателей, близкого к оптимальному по указанным показателям.

Методика исследования заключается в математическом моделировании трех этапов аварийной ситуации, состоящих в следующем:

-          первый этап длительностью Δt₁ ≈ 0.14 … 0.2 с (с момента касания до отключения сети защитой от утечек);

-          второй этап Δt₂ ≈ 0.2…0.33с начинается моментом отключения сети и длится до отключения контакторов потребителей вследствие снижения генерируемой двигателями эдс;

-          третий этап длительностью Δt₁ ≈ 0.2…0.6с заканчивается, когда после отключения контакторов эдс оставшегося двигателя снижается до безопасного уровня.

Общая длительность трех этапов составляет Δt₁ + Δt₂ + Δt₃ ≈ 0.95…1.15 с [1–3]. Текущее значение эквивалентного тока I_е (среднеквадратичного за время действия t_д) находится из выражения

,                                                                      (1)

где i – мгновенное значение тока утечки;

а количество поглощенной телом человека электромагнитной энергии Q_е(t) из выражения

.                                                          (2)

Принятые допущения:

1.      До повреждения или касания человеком токоведущего звена сеть симметрична.

2.      ЭДС статора двигателя в режиме выбега является синусоидальной, ее амплитуда пропорциональна магнитному потоку ротора и его частоте вращения.

3.      Электрическая цепь ротора эквивалентного генератора является инерционным звеном первого порядка, интенсивность затухания потока которого характеризуется постоянной времени Т_Е.

4.      Закон изменения частоты вращения ротора в режиме свободного выбега является линейным и определяется механической постоянной времени Т_М, равной среднему времени выбега.

5.      Сопротивление тела человека R_h неизменное, активное и равно 1000 Ом.

В силу принятых допущений частоту вращения ротора двигателя можно описать выражением (отсчет времени с момента срабатывания защитного отключения):

                                              (3)

            где ω, ω₀ – текущая и синхронная частоты вращения ротора;

s_n – начальное (номинальное) скольжение двигателя (эквивалентного генератора) в момент отключения сети.

Амплитуда фазной ЭДС двигателя E_max(t) представляется выражением:

,                    (4)

где k_е = 0,9…0,95 – коэффициент, учитывающий отношение начального значения ЭДС двигателя по отношению к напряжению сети U.

Так как закон изменения ЭДС можно считать синусоидальным, хотя и с переменными амплитудой и частотой, ее фазу, однозначно зависящую от угла поворота ротора φ(t), определяем выражением:

,                                          (5)

где ψ_р – значение фазы ЕДС двигателя в момент начала второго этапа.

Таким образом окончательное выражение, моделирующее ЭДС двигателя в режиме выбега, имеет вид:

                    (6)

Эквивалентные схемы замещения участковой шахтной сети с компенсацией емкостных токов утечки приведены на рис. 1 а, б. Они отличаются сопротивлениями, образующими фильтр нулевой последовательности (ФНП) для подключения компенсирующего дросселя. На схеме рис. 1 а для этой цели использованы емкости С_F , а на схеме рис. 1 б – катушки индуктивности L_F, R_F.

На схемах рис. 1 обозначено: R, С – сопротивления изоляции и емкости фаз кабелей по отношению к земле; L_Д, R_Д – индуктивность и активное сопротивление компенсирующего дросселя; C_P – разделительная емкость; i_h , R_h – ток и сопротивление в месте повреждения.

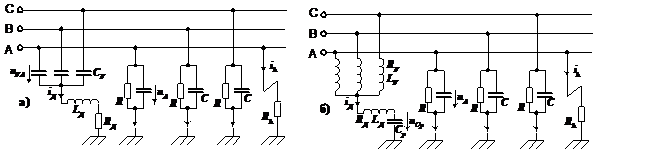
Рисунок 1. Схемы компенсации емкостной составляющей токов утечки с емкостным (а) и индуктивным (б) фильтрами нулевой последовательности.

Цепь рис. 1 а в динамике (первый этап) определяется тремя переменными состояния и представляется следующей математической моделью:

                                                              ;

;                                                          (7)

                                                                ,

где i_Д , u_А , u_FА  –  мгновенные значения переменных состояния (ток дросселя, напряжение фазы А силовой сети, напряжение фазы А ФНП);

e_А = E_m·sin(ωt + ψ) – мгновенное значение эквивалентной ЭДС фазы А источника питания;

ψ – начальная фаза, определяющая момент коммутации.

Математическая модель схемы рис. 1 б имеет вид:

                                                               ;

;                                                                     (8)

                                                                ,

где u_Сp  –  мгновенное значение напряжения на разделительной емкости С_р.

Для второго этапа в системах уравнений (7) и (8) напряжение сети заменяется эквивалентной ЭДС двигателей в режиме выбега согласно (6), причем, значения переменных состояния в конце первого этапа берутся в качестве независимых начальных условий начала второго этапа.

На третьем этапе из систем (7), (8) исключаются параметры, представляющие цепь компенсации и фильтр нулевой последовательности, в 3…5 раз уменьшается емкость С “фаза–земля“ и пропорционально увеличивается сопротивление изоляции R.

Фактическая длительность второго этапа Δt₂ зависит от множества факторов, однако связанная с постоянными времени Т_Е и Т_М может быть определена из выражения (4) для условия, что ЭДС двигателей (эквивалентного генератора) в режиме выбега снижается до значения, необходимого для отключения контакторов.

Результаты выполненных по этому условию расчетов приведены на рис. 2. Механическая постоянная времени изменялась в пределах от 0.5 до 5 с при фиксированных значениях 0.75, 1.0, 1.25, 1.5 с электромагнитной постоянной времени. Значение Δt₂ оказалось в пределах от 0.15 до 0.4 с.

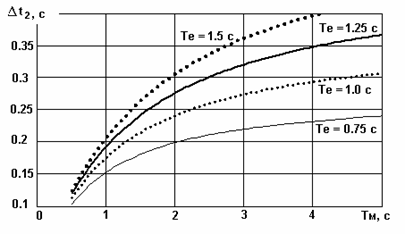
Рис. 2. Расчетные значения длительности второго этапа

в зависимости от значений постоянных времени Т_Е  и  Т_М.

Одна из расчетных осциллограмм численного эксперимента для участковой шахтной сети (U = 660 В, С = 0.75 мкФ, Т_Е = Т_М = 2 с, дроссель неуправляем, ФНП индуктивный), приведена на рис. 3. В данном эксперименте индуктивность компенсирующего дросселя постоянна на первом и втором этапах и равна резонансному значению при f = 50 Гц, т.е. L_Д/L₀ = 1 (L₀ – резонансная индуктивность дросселя на первом этапе). Обращают на себя внимание резкие броски тока и подъемы кривой Q_е(t) при первой (t = 0) и второй (t = 0.2 с) коммутациях. На втором этапе (0.2 < t < 0.45 с), где компенсация нарушена, наблюдается нарастание тока и количества поглощенной телом человека электромагнитной энергии, несмотря на снижение ЭДС двигателей.

Опыты, аналогичные эксперименту рис. 3, проводились при различных значениях отношения L/L₀ для неуправляемого дросселя на первом и втором этапах. Что касается управляемого дросселя, то на первом этапе обеспечивалась полная компенсация (резонанс токов), а на втором этапе имитировался неуправляемый режим при различных значениях отношения L/L₀, являвшегося аргументом исследования.

Рис. 3. Расчетные осциллограммы i(t), Q_е(t), I_е(t) для условий:

U = 660 В, С = 0.75 мкФ, Т_Е = Т_М = 2 с, дроссель неуправляем.

На рис. 4 приведены зависимости количества поглощенной телом человека электромагнитной энергии от значения компенсирующей индуктивности в соответствии с описанной методикой. Как уже отмечалось, при допущении, что сопротивление тела человека неизменно (1000 Ом), между значениями Q и эквивалентного тока существует однозначное соответствие (2).

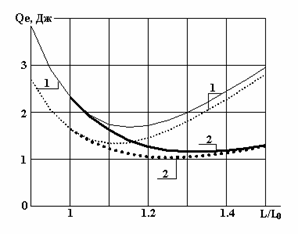
Рисунок  4. Зависимости поглощенной человеком энергии от индуктивности дросселя.

1 – дроссель неуправляем; 2 – дроссель управляем; сплошные линии – индуктивный ФНП; пунктир – емкостный ФНП.

Как следует из полученных результатов (рис. 4), минимум Q для неуправляемого дросселя с емкостным ФНП отвечает условию L/L₀,≈ 1.1 и составляет Q = 1.3 Дж (I_е = 33 мА). В схеме с индуктивным ФНП минимум Q отвечает условию L/L₀,≈ 1.15 и составляет Q = 1.6 Дж (I_е = 37 мА). Лучшие результаты дает управляемая компенсация. При завышении индуктивности дросселя на втором этапе на 25…35% поглощенная энергия составляет 1…1.15 Дж (I_е = 29…31 мА). Хотя эти результаты при длительности воздействия тока, не превышающей 1 с, по эквивалентному току соответствуют требованиям [5], на практике не всегда удается оптимизировать режим компенсации.

Представляет интерес “доля“ поглощенной энергии, вносимая переходными процессами. На рис. 5 приведены осциллограммы исследуемых величин начала первого этапа для схемы с индуктивным ФНП. Исследование выполнено для трех различных значений начальной фазы коммутации ψ.

Обращает на себя внимание рост поглощенной энергии (и эквивалентного тока) при ψ → 0. Причем, расхождение достигает 16…18% по отношению к условию ψ = 90⁰. Исходя из практической длительности переходного процесса на уровне от 0,025 с.до.0,030 с, “доля“ поглощенной энергии составляет Q = 0.4…0.48 Дж (I_е = 121…132 мА за время длительности переходного процесса). Аналогичное исследование схемы с емкостным ФНП дало результаты Q = 0.44…0.48 Дж (I_е = 126…132 мА). Во всех опытах большему значению Q соответствует нулевая начальная фаза. Переходный процесс в начальной стадии второго этапа приносит добавку поглощенной энергии в пределах 0.05…0.2 Дж, а суммарная составляющая двух переходных режимов достигает 0.6…0.65 Дж (максимумы энергии первого и второго этапов не совпадают). Переходный процесс на третьем этапе не выражен и практически не наблюдается.

Рис. 5. Осциллограммы переходного процесса на первом этапе при различных начальных фазах коммутации (схема с индуктивным ФНП, базовый вариант).

Можно утверждать, что суммарная составляющая поглощенной телом человека энергии, обусловленная переходными процессами, практически не зависит от схемы ФНП или режима компенсации. Тем не менее, установлено, что эта величина находится в квадратичной зависимости от емкости кабелей и напряжения сети. Это значит, что хотя исследуемые системы формально являются нелинейными (из-за нелинейности, вносимой ЭДС двигателей (5) при выбеге), по отношению к поглощенной телом человека энергии и эквивалентному току они ведут себя практически так же, как линейные системы.

Вывод: Исследование применимо к сетям с изолированной нейтралью с защитным отключением и компенсацией емкостной составляющей тока утечки, нагрузкой которых являются в основном асинхронные электродвигатели. Предложенные методика и математические модели предусматривают анализ трех этапов развития аварийной ситуации при попадании человека под фазное напряжение, позволяют получить мгновенное и текущее эквивалентное (среднеквадратичное) значение тока, протекающего через тело человека, а при допущении о постоянстве электрического сопротивления последнего оценить количество электромагнитной энергии, поглощенной его телом за время действия тока. Эта информация может быть использована для предварительной оценки степени опасности сети для человека, оказавшегося под напряжением, выбора типа компенсирующего устройства и определения режима его работы, оптимального с точки зрения минимума эквивалентного тока и количества поглощенной энергии. Она также необходима при анализе организационных и технических мероприятий, снижающих степень опасности исследуемой сети для человека, оказавшегося под фазным напряжением.

ЛИТЕРАТУРА

1.      Дзюбан В.С., Риман Я.С. Метод расчета кратковременного безопасного тока. – В кн. Взрывобезопасное электрооборудование. Вып. 6 М., Энергия, 1969.

2.      Чорноус Е.В., Ковалев А.П., Чорноус  В.П. Об оценке электробезопасности сети с изолированной нейтралью.           “Электричество“       2006     № 5         с. 59 – 62.

3.      Дзюбан В.С., Риман Я.С. Об электромагнитной постоянной времени затухания обратной э.д.с. шахтных электродвигателей. – В кн. Взрывобезопасное электрооборудование. Вып. 6 М., Энергия, 1969.

4.      Айдаров Ф. А. О требуемых характеристиках дросселей устройств автоматической компенсации емкостных токов утечек в подземных низковольтных сетях.