УДК 621.3.05:519.2
ІНЕРЦІЙНЕ ЕНЕРГЕТИЧНЕ ЗГЛАДЖУВАННЯ ВИПАДКОВИХ ЕЛЕКТРИЧНИХ ПРОЦЕСІВ
Е.Г. Курінний, докт. техн. наук, Н.М. Погрібняк (Донецьк. держ. техн. ун-т, Донецьк)
Розглянуто типову задачу оцінки впливу випадкових електричних процесів на мережі та електроприймачі. На прикладі розрахунку температури перегріву провідника дається рішення шляхом імітації випадкових електричних навантажень.Рассмотрена типичная задача оценки воздействий случайных электрических процессов на сети и электроприемники. На примере расчета температуры перегрева проводника дается решение путем имитации случайных электрических нагрузок.
Вихідні положення. Якщо оцінюється вплив електричних процесів на мережу та електроприймачі, то потрібно враховувати, принаймні, потужність процесів і інерційність об’єктів. Тому в теорії електромагнітної сумісності типовою є задача про інерційне енергетичне згладжування [7], яка полягає в знаходженні характеристик рішення лінійного диференціального рівняння першого порядку, до правої частини якого входить квадрат досліджуваного випадкового процесу.
Існуючі аналітичні рішення у вигляді рядів не завжди придатні до практичного застосування, тому потрібно переходити до методів імітації. Для визначеності розглянемо задачу оцінки температури
 перегріву провідника випадковим електричним
навантаженням
перегріву провідника випадковим електричним
навантаженням  з
експоненційною кореляційною функцією
(КФ).
з
експоненційною кореляційною функцією
(КФ).У теорії електричних навантажень [8] застосовується спрощене рівняння перегріву провідника
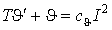 ,(1)
,(1)
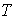 - стала часу нагріву,
- стала часу нагріву, 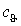 - постійний коефіцієнт
у °С/А2. Для зручності введемо пропорційну температурі
величину “гріючої дози”
- постійний коефіцієнт
у °С/А2. Для зручності введемо пропорційну температурі
величину “гріючої дози” 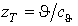 в А2 і “гріючого навантаження”
в А2 і “гріючого навантаження”  у А. Тоді замість (1)
вихідним буде рівняння
у А. Тоді замість (1)
вихідним буде рівняння
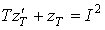 .(2)
.(2)
 доз. По ній
визначається розрахункове максимальне значення
доз. По ній
визначається розрахункове максимальне значення  доз, яке може
перевищуватися лише з заданою малою імовірністю
доз, яке може
перевищуватися лише з заданою малою імовірністю 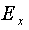 . Далі, як і в [4],
прийняте значення
. Далі, як і в [4],
прийняте значення 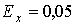 . Розрахунковим навантаженням з перегріву є максимум
. Розрахунковим навантаженням з перегріву є максимум
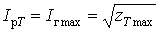 (3)
(3)
Процес
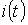 змінення електричного
навантаження електроприймача являє собою послідовність прямокутних
імпульсів величиною
змінення електричного
навантаження електроприймача являє собою послідовність прямокутних
імпульсів величиною  і нульових пауз з випадковими тривалостями
і нульових пауз з випадковими тривалостями 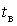 імпульсів і
імпульсів і  пауз. Інтенсивність
пауз. Інтенсивність
 потоку вмикань
або вимикань обернена середній тривалості циклу. Коефіцієнт вмикання
потоку вмикань
або вимикань обернена середній тривалості циклу. Коефіцієнт вмикання
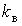 є імовірність
вмикненого стану електроприймача, а коефіцієнт вимикання
є імовірність
вмикненого стану електроприймача, а коефіцієнт вимикання  - імовірність паузи.
Через ці характеристики виражаються середнє і ефективне значення, а
також стандарт навантаження:
- імовірність паузи.
Через ці характеристики виражаються середнє і ефективне значення, а
також стандарт навантаження:
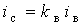 ,
,
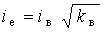 ,
, 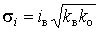 .(4)
Індивідуальне навантаження має
експоненціальну КФ
.(4)
Індивідуальне навантаження має
експоненціальну КФ
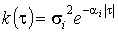
 ,
якщо розподіли тривалостей імпульсів і пауз будуть показовими, які
визначаються їх середніми значеннями
,
якщо розподіли тривалостей імпульсів і пауз будуть показовими, які
визначаються їх середніми значеннями  і
і 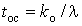 .
.Процес
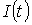 змінення сумарного
навантаження групи масових електроприймачів має нормальний розподіл
з середнім значенням
змінення сумарного
навантаження групи масових електроприймачів має нормальний розподіл
з середнім значенням  і стандартом
і стандартом 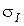 , а також експоненційну КФ
, а також експоненційну КФ
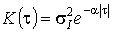 (5)
(5)
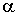 .
.Розрахункове значення випадкової величини
 (або
(або 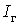 , якщо
, якщо 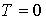 ) визначають у вигляді виразу
) визначають у вигляді виразу
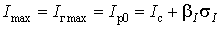 ,
(6)
,
(6)
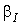 і імовірністю
і імовірністю 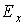 є відомим. Це можливо, коли відомим є розподіл
випадкової величини. Для нормального розподілу
є відомим. Це можливо, коли відомим є розподіл
випадкової величини. Для нормального розподілу 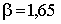 , якщо
, якщо  .
.Аналітичні рішення. У явному вигляді аналітичне рішення задачі згладжування може бути знайдено лише для поодинокого випадку індивідуального навантаження з експоненційною КФ і
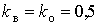 . Для цього достатньо
застосувати відому формулу для щільності розподілу ординат
. Для цього достатньо
застосувати відому формулу для щільності розподілу ординат 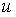 інерційного
згладжування телеграфного сигналу [3]:
інерційного
згладжування телеграфного сигналу [3]:
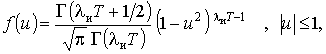
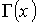 -
гамма-функція,
-
гамма-функція, 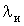 -
інтенсивність точок пересічення осі абсцис
(нулів).
-
інтенсивність точок пересічення осі абсцис
(нулів).У розглядаємому випадку
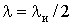 ,
, 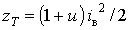 . Підставивши ці вирази
в відому загальну формулу теорії імовірностей для функціонального
перетворення випадкового аргументу, знайдемо щільність розподілу доз
. Підставивши ці вирази
в відому загальну формулу теорії імовірностей для функціонального
перетворення випадкового аргументу, знайдемо щільність розподілу доз
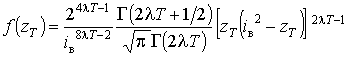 (7)
(7)
 . Аналогічно знаходиться рішення, коли замість пауз
є ділянки холостого ходу. Слід визначити, що формула (7) уточнює
наведений в п.II.6 монографії [7] вираз для щільності доз, у якому
потрібно замінити
. Аналогічно знаходиться рішення, коли замість пауз
є ділянки холостого ходу. Слід визначити, що формула (7) уточнює
наведений в п.II.6 монографії [7] вираз для щільності доз, у якому
потрібно замінити 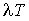 на
на 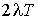 .
.У інших випадках рішення знаходять у вигляді ряду Еджворта [5] через функцію
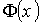 стандартного
нормального розподілу, її похідні та центральні моменти
стандартного
нормального розподілу, її похідні та центральні моменти  розподілу доз.
Враховуючи, що середнє значення гріючих доз дорівнює квадрату
ефективного навантаження
розподілу доз.
Враховуючи, що середнє значення гріючих доз дорівнює квадрату
ефективного навантаження або
або  , запишемо ряд Еджворта у вигляді
, запишемо ряд Еджворта у вигляді
 ,(8)
,(8)
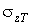 - стандарт доз,
- стандарт доз, 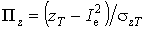 ,
, 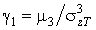 і
і  є асиметрія і
ексцес доз. Відзначимо, що в формулу (8) аргумент
є асиметрія і
ексцес доз. Відзначимо, що в формулу (8) аргумент 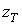 неявно через
неявно через  .
.Враховуючи, що
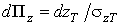 , інтегруванням
виразу (8) у межах від
, інтегруванням
виразу (8) у межах від 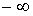 до
до  знайдемо функцію розподілу доз
знайдемо функцію розподілу доз
 (9)
(9)
Ряд Еджворта дає необмежений розподіл імовірностей від
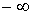 до
до  , в той час як доза може бути обмеженою в діапазоні
, в той час як доза може бути обмеженою в діапазоні
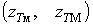 . Для врахування
обмеженості перейдемо до зрізаного розподілу, який відрізняється
коефіцієнтом
. Для врахування
обмеженості перейдемо до зрізаного розподілу, який відрізняється
коефіцієнтом
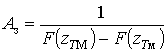 .
.
 ,(10)
,(10)
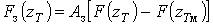 .(11)
.(11)
 , то відповідно (7)
розподіл доз буде рівномірним:
, то відповідно (7)
розподіл доз буде рівномірним: 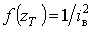 (пряма 1 на рис.1), для якого
(пряма 1 на рис.1), для якого  ,
, 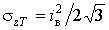 ,
,  ,
, 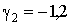 . Розрахунки по формулі
(8) дали криву 2, яка не тільки відрізняється від прямої 1, але
виходить за межі
. Розрахунки по формулі
(8) дали криву 2, яка не тільки відрізняється від прямої 1, але
виходить за межі 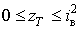 ,
що суперечить фізичному глузду. Дійсно, площини областей а і б
становлять 0,045, тому при
,
що суперечить фізичному глузду. Дійсно, площини областей а і б
становлять 0,045, тому при 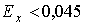 від’ємна область а дає мнимі мінімальні
навантаження
від’ємна область а дає мнимі мінімальні
навантаження 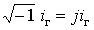 , а
область б - максимальні навантаження, які перевищують
, а
область б - максимальні навантаження, які перевищують 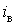 , чого не може бути. І
хоча при
, чого не може бути. І
хоча при 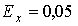 розраховане по ряду максимальне навантаження 0,993
розраховане по ряду максимальне навантаження 0,993 усього на 1,85%
перевищує теоретичне значення 0,975
усього на 1,85%
перевищує теоретичне значення 0,975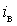 , це не може свідчити на користь можливості
застосування ряду Еджворта, бо з цією ж вірогідністю ряд на 37,1%
занижує мінімальне навантаження (0,141
, це не може свідчити на користь можливості
застосування ряду Еджворта, бо з цією ж вірогідністю ряд на 37,1%
занижує мінімальне навантаження (0,141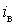 проти теоретичного
значення 0,224
проти теоретичного
значення 0,224 ),
тобто більш, ніж втричі перевищує допустиму
похибку.
),
тобто більш, ніж втричі перевищує допустиму
похибку.Формула (10) при
 і
і 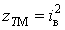 дає криву 3, яка
знаходиться в діапазоні змінення доз. В цьому випадку максимальне і
мінімальне значення становлять
дає криву 3, яка
знаходиться в діапазоні змінення доз. В цьому випадку максимальне і
мінімальне значення становлять 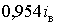 та
та 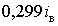 , тобто на -2,15 та 33,5% відрізняються від
теоретичних.
, тобто на -2,15 та 33,5% відрізняються від
теоретичних.Методика імітації. Існує велика кількість методів імітації випадкових процесів, із яких природно застосовувати методи, відображаючи фізику розв’язування задачі. Оскільки процеси в системах електропостачання ергодичні, їх можливо імітувати у вигляді однієї реалізації. Однак, не зважаючи на більшу наочність імітації «по реалізації», все ж доцільніше імітувати випадкові процеси у вигляді ансамблю реалізацій. Це дозволяє отримувати характеристики стаціонарного режиму одразу після закінчення перехідного процесу (приблизно через 5 - 6
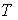 ), а також
вивчати перехідний процес змінень
доз.
), а також
вивчати перехідний процес змінень
доз.Кожна реалізація доз розраховується по реалізації навантаження відповідно з інтегралом Дюамеля, починаючи з нульового значення дози
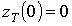 . Статистична функція
. Статистична функція
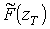 або щільність
або щільність
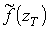 розподілу та інші
характеристики доз (знак ~) для потрібного моменту часу
розраховуються по перерізу
ансамблю.
розподілу та інші
характеристики доз (знак ~) для потрібного моменту часу
розраховуються по перерізу
ансамблю.Точність імітації забезпечується вибором великої кількості
 реалізацій у
відповідності з відомими методами оцінки погрішностей відтворення
тих або інших характеристик. Доцільно перевіряти точність імітації
для поодиноких випадків, коли аналітичне рішення
відомо.
реалізацій у
відповідності з відомими методами оцінки погрішностей відтворення
тих або інших характеристик. Доцільно перевіряти точність імітації
для поодиноких випадків, коли аналітичне рішення
відомо.Теоретично можливо, але малоймовірно, що в силу псевдовипадковості роботи датчиків випадкових чисел між реалізаціями виникне зв’язок. Для виключення цього слід імітувати
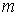 ансамблів по
ансамблів по 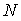 реалізацій в кожному, а шукані характеристики
знаходити як середні значення по
реалізацій в кожному, а шукані характеристики
знаходити як середні значення по  . Досвід показує, що достатньо прийняти
. Досвід показує, що достатньо прийняти 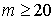 .
.Індивідуальні процеси. Для імітації індивідуального графіку навантаження з експоненційною КФ було застосовано два «пускових» і
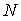 «робочих» датчиків
випадкових чисел, що імітують рівномірно розподілені на інтервалі
(0, 1) випадкові величини
«робочих» датчиків
випадкових чисел, що імітують рівномірно розподілені на інтервалі
(0, 1) випадкові величини 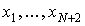 . Один пусковий датчик задає
. Один пусковий датчик задає 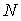 початкових чисел
початкових чисел 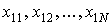 для запуску робочих
датчиків. Другий пусковий датчик встановлює початкові значення
навантаження кожної
для запуску робочих
датчиків. Другий пусковий датчик встановлює початкові значення
навантаження кожної 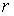 - ої реалізації:
- ої реалізації: 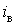 , якщо
, якщо 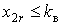 , і нуль - в протилежному випадку. Показові
розподіли тривалостей імпульсів і пауз одержуються логарифмічним
перетворенням випадкових чисел від робочих датчиків:
, і нуль - в протилежному випадку. Показові
розподіли тривалостей імпульсів і пауз одержуються логарифмічним
перетворенням випадкових чисел від робочих датчиків:  .
.Реалізації доз являють собою послідовність криволінійних відрізків. Якщо в момент часу
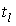 починається
імпульс навантаження випадкової тривалості
починається
імпульс навантаження випадкової тривалості  , а початкове значення
дози дорівнює
, а початкове значення
дози дорівнює 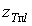 , то
відрізок розраховується за формулою
, то
відрізок розраховується за формулою
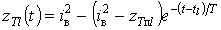 .
.
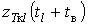 буде початковою для
наступного відрізку. Для паузи в формулі замість
буде початковою для
наступного відрізку. Для паузи в формулі замість 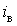 потрібно підставити
нуль.
потрібно підставити
нуль.Імітація ансамблів з
 дозволила отримати
залежності розрахункових навантажень
дозволила отримати
залежності розрахункових навантажень  від
від 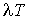 або
або 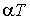 (рис. 2), оскільки
параметр
(рис. 2), оскільки
параметр 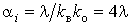 [7]. При
[7]. При
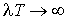 криві прагнуть до
величини ефективного навантаження (пунктир на рис. 2). Аналітичне же
рішення у вигляді (7) є лише при
криві прагнуть до
величини ефективного навантаження (пунктир на рис. 2). Аналітичне же
рішення у вигляді (7) є лише при 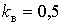 . Для цього випадку статистичні значення
відрізняються від теоретичних не більш, як на 1,31%. На рис.1
показана гістограма 4 процесу змінення доз, яка була отримана
імітацією. Її відмінність від теоретичної прямої 1 незначна, що
підтверджується перевіркою критерієм
Пірсона.
. Для цього випадку статистичні значення
відрізняються від теоретичних не більш, як на 1,31%. На рис.1
показана гістограма 4 процесу змінення доз, яка була отримана
імітацією. Її відмінність від теоретичної прямої 1 незначна, що
підтверджується перевіркою критерієм
Пірсона.Нормальні процеси. Реалізації нормального випадкового процесу з експоненціальною КФ можливо отримати різними методами. Найбільш повно фізичну суть формування навантаження групи електроприймачів відображає метод елементних процесів [7], за яким імітація здійснюється у вигляді суми
 елементних
процесів з КФ
елементних
процесів з КФ
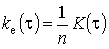 .
.
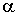 , тому для її отримання істотно взяти розглянуту
вище послідовність прямокутних імпульсів і пауз з показовими
розподілами тривалостей.
, тому для її отримання істотно взяти розглянуту
вище послідовність прямокутних імпульсів і пауз з показовими
розподілами тривалостей.Сума елементних процесів дає біноміальний розподіл навантаження, який при великому
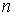 наближається до нормального: тим краще, чим менше величина
наближається до нормального: тим краще, чим менше величина  . Якщо
. Якщо  однакові, збіжність
найкраща при
однакові, збіжність
найкраща при 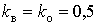 , що
і прийнято далі. У довіднику [1] дається максимальна оцінка
, що
і прийнято далі. У довіднику [1] дається максимальна оцінка  , яка веде до
нерівності
, яка веде до
нерівності 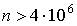 . Така
велика кількість елементних процесів може знадобитись, коли у правій
частині вихідного диференціального рівняння будуть похідниці. У
розгляданому випадку цього нема, тому збіжність до нормального
розподілу будемо оцінювати по близькості статистичного коефіцієнту
. Така
велика кількість елементних процесів може знадобитись, коли у правій
частині вихідного диференціального рівняння будуть похідниці. У
розгляданому випадку цього нема, тому збіжність до нормального
розподілу будемо оцінювати по близькості статистичного коефіцієнту
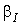 до значення 1,65.
Розрахунки показали, що з прийнятою в теорії електричних навантажень
допустимою похибкою 10% потрібно
до значення 1,65.
Розрахунки показали, що з прийнятою в теорії електричних навантажень
допустимою похибкою 10% потрібно 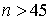 , а 5% -
, а 5% - 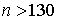 .
.Середнє значення доз

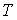 . Можна показати , що для нормального процесу з
експоненціальною КФ (5) дисперсія доз розраховується згідно з
формулою
. Можна показати , що для нормального процесу з
експоненціальною КФ (5) дисперсія доз розраховується згідно з
формулою
 .(12)
.(12)
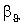 для температур, який збігається із статистичним
коефіцієнтом
для температур, який збігається із статистичним
коефіцієнтом 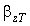 для
доз:
для
доз:
 ,(13)
,(13)
 величина
величина 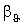 є невизначеною, бо не
відомий закон розподілу доз.
є невизначеною, бо не
відомий закон розподілу доз.Для визначення величини
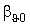 при
при  для квадратичного перетворювання
для квадратичного перетворювання  застосуємо загальні
формули (II.11) та (II.12) з [7]. В результаті отримаємо функцію
розподілу нульових доз:
застосуємо загальні
формули (II.11) та (II.12) з [7]. В результаті отримаємо функцію
розподілу нульових доз:
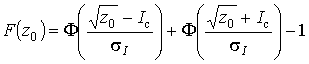 ,(14)
,(14)
 .
.
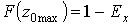 , знайдемо
розрахунковий максимум
, знайдемо
розрахунковий максимум 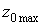 , а також статистичний коефіцієнт
, а також статистичний коефіцієнт
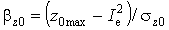 .
.
 у відносних одиницях важко, тому у кожному
конкретному випадку знадобиться імітація з фактичними значеннями
у відносних одиницях важко, тому у кожному
конкретному випадку знадобиться імітація з фактичними значеннями
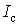 і
і 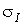 . Як приклад розглянемо
імітацію десятихвилинних доз з
. Як приклад розглянемо
імітацію десятихвилинних доз з 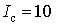 А,
А,  А і
А і 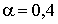 хв-1, тобто
хв-1, тобто  .
.Приймемо
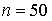 ,
, 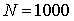 і
і 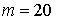 . Для визначення
характеристик доз у стаціонарному режимі візьмемо період
. Для визначення
характеристик доз у стаціонарному режимі візьмемо період 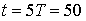 хв. По 1000 ординатах
перерізу була знайдена гістограма доз 1 (рис. 3). Це дозволило
отримати різні статистичні характеристики, а також потрібне значення
хв. По 1000 ординатах
перерізу була знайдена гістограма доз 1 (рис. 3). Це дозволило
отримати різні статистичні характеристики, а також потрібне значення
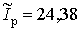 А.
А.Формула (8) дає криву 2, яка суттєво відрізняється від гістограми, а в початковій стадії суперечить фізичному глузду, бо має не тільки абсциси
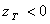 , але й від’ємні
ординати. Більш того, від’ємну область при
, але й від’ємні
ординати. Більш того, від’ємну область при  має і функція
розподілу, тому при малих
має і функція
розподілу, тому при малих 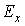 виникає неоднозначність у знаходженні мінімальних
навантажень: наприклад, імовірності
виникає неоднозначність у знаходженні мінімальних
навантажень: наприклад, імовірності 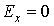 замість теоретичного
значення 0 відповідають три мінімальні навантаження:
замість теоретичного
значення 0 відповідають три мінімальні навантаження: 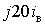 ,
, 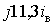 ,
,  . Проте в зоні
максимальних навантажень розбіжності між статистичними і знайденими
по ряду значеннями малі, а при
. Проте в зоні
максимальних навантажень розбіжності між статистичними і знайденими
по ряду значеннями малі, а при 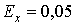 практично розрахункові навантаження збігаються.
Розрахована згідно з формулою (10) крива 3 знаходиться у межах
змінення доз:
практично розрахункові навантаження збігаються.
Розрахована згідно з формулою (10) крива 3 знаходиться у межах
змінення доз:  .
Хоча розрахункові значення теж достатньо близьки до статистичних,
але щільність розподілу поблизу нуля від’ємна, чого не може бути.
Таким чином, при нормальних навантаженнях ряди Еджворта можливо
використовувати для орієнтовних оцінок максимальних значень, але аж
ніяк для приймання остаточних
рішень.
.
Хоча розрахункові значення теж достатньо близьки до статистичних,
але щільність розподілу поблизу нуля від’ємна, чого не може бути.
Таким чином, при нормальних навантаженнях ряди Еджворта можливо
використовувати для орієнтовних оцінок максимальних значень, але аж
ніяк для приймання остаточних
рішень.Імітація для інших сталих часу дозволила отримати залежності розрахункових навантажень та інших характеристик від
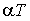 , які частково представлені на рис.4, де кружками
показані теоретичні значення при
, які частково представлені на рис.4, де кружками
показані теоретичні значення при 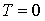 . Із зростанням
. Із зростанням  розрахункове навантаження зменшується, прагнучи
досягти значення
розрахункове навантаження зменшується, прагнучи
досягти значення 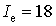 А. Якісно інерційні системи нормалізують процеси на їх виходах,
проте в розгляданій задачі ця нормалізація іде дуже повільно: навіть
при достатньо великих
А. Якісно інерційні системи нормалізують процеси на їх виходах,
проте в розгляданій задачі ця нормалізація іде дуже повільно: навіть
при достатньо великих 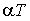 статистичний коефіцієнт перевищує значення 1,65, а
асиметрія та ексцес не дорівнюють
нулю.
статистичний коефіцієнт перевищує значення 1,65, а
асиметрія та ексцес не дорівнюють
нулю.Не зважаючи на невелику кількість
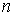 і
великий коефіцієнт форми
і
великий коефіцієнт форми 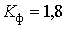 , похибки відтворення характеристик виявилися
невеликими: від -1,27 до 1,1% для
, похибки відтворення характеристик виявилися
невеликими: від -1,27 до 1,1% для 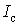 , від -0,56 до 1,06% для
, від -0,56 до 1,06% для  , від -1,53 до 1,87%
для
, від -1,53 до 1,87%
для  , від -1,34 до
1,73% для величини
, від -1,34 до
1,73% для величини 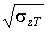 .
.Висновок. Обмеженість вихідної інформації не дозволяє використовувати ряди Еджворта для рішення задачі про інерційне енергетичне згладжування, яку потрібно розраховувати методами імітації випадкових електроенергетичних процесів.
1. Анго А. Математика для электро- и радиоинженеров. - М.: Наука, 1965. - 778 с.
2. Васильев Д.В. Инерционное детектирование случайной последовательности прямоугольных импульсов // Известия высших учебных заведений, - 1960, т. 3, №6. - С.1010 - 1021.
3. Горяинов В.Т., Журавлев А.Г., Тихонов В.П. Примеры и задачи по статистической радиотехнике. - М.: Советское радио, 1970. - 597 с.
4. ГОСТ 13109-87. Электрическая энергия. Требования к качеству электрической энергии в электрических сетях общего назначения. - Введ. 01.01.89.
5. Edgeworth F.Y. The law of error. - Proc. Cambridge Phil. Soc., 1905, v. 20. - P. 36 - 65.
6. Свешников А.А. Прикладные методы теории случайных функций. - М.: Наука, 1968. - 463 с.
7. Шидловский А.К., Куренный Э.Г. Введение в статистическую динамику систем электроснабжения. - К.: Наукова думка, 1984. - 271 с.
8. Электромагнитная совместимость электроприемников промышленных предприятий/ А.К.Шидловский (ред.). - Киев: Наукова думка. 1992. - 236 с.
Аналітичні рішення. У явному вигляді аналітичне рішення задачі згладжування може бути знайдено лише для поодинокого випадку індивідуального навантаження з експоненційною КФ і
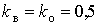 . Для цього достатньо застосувати відому формулу для
щільності розподілу ординат
. Для цього достатньо застосувати відому формулу для
щільності розподілу ординат 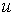 інерційного згладжування телеграфного сигналу [3]:
інерційного згладжування телеграфного сигналу [3]:
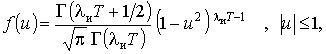
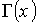 - гамма-функція,
- гамма-функція, 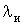 - інтенсивність точок пересічення осі абсцис
(нулів).
- інтенсивність точок пересічення осі абсцис
(нулів).У розглядаємому випадку
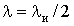 ,
, 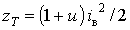 . Підставивши ці вирази
в відому загальну формулу теорії імовірностей для функціонального
перетворення випадкового аргументу, знайдемо щільність розподілу доз
. Підставивши ці вирази
в відому загальну формулу теорії імовірностей для функціонального
перетворення випадкового аргументу, знайдемо щільність розподілу доз
 (7)
(7)
 . Аналогічно знаходиться рішення, коли замість пауз
є ділянки холостого ходу. Слід визначити, що формула (7) уточнює
наведений в п.II.6 монографії [7] вираз для щільності доз, у якому
потрібно замінити
. Аналогічно знаходиться рішення, коли замість пауз
є ділянки холостого ходу. Слід визначити, що формула (7) уточнює
наведений в п.II.6 монографії [7] вираз для щільності доз, у якому
потрібно замінити 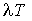 на
на 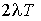 .
.У інших випадках рішення знаходять у вигляді ряду Еджворта [5] через функцію
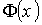 стандартного
нормального розподілу, її похідні та центральні моменти
стандартного
нормального розподілу, її похідні та центральні моменти 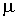 розподілу доз.
Враховуючи, що середнє значення гріючих доз дорівнює квадрату
ефективного навантаження
розподілу доз.
Враховуючи, що середнє значення гріючих доз дорівнює квадрату
ефективного навантаження або
або  , запишемо ряд Еджворта у вигляді
, запишемо ряд Еджворта у вигляді
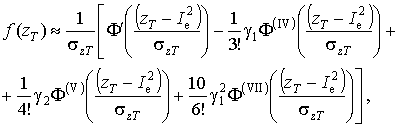 (8)
(8)
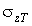 - стандарт доз,
- стандарт доз, 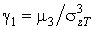 і
і 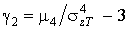 є асиметрія і ексцес доз. Відзначимо, що в формулу
(8) аргумент
є асиметрія і ексцес доз. Відзначимо, що в формулу
(8) аргумент  неявно через
неявно через 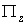 .
.Інтегруванням виразу (8) у межах від
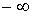 до
до  знайдемо функцію розподілу доз
знайдемо функцію розподілу доз
 (9)
(9)
Ряд Еджворта дає необмежений розподіл імовірностей від
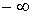 до
до  , в той час як доза може бути обмеженою в діапазоні
, в той час як доза може бути обмеженою в діапазоні
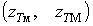 . Для врахування
обмеженості перейдемо до зрізаного розподілу, який відрізняється
коефіцієнтом
. Для врахування
обмеженості перейдемо до зрізаного розподілу, який відрізняється
коефіцієнтом
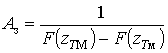 .
.
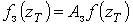 ,(10)
,(10)
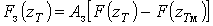 .(11)
.(11)
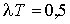 , то відповідно (7)
розподіл доз буде рівномірним:
, то відповідно (7)
розподіл доз буде рівномірним: 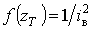 (пряма 1 на рис.1), для якого
(пряма 1 на рис.1), для якого 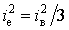 ,
,  ,
, 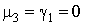 ,
,  . Розрахунки по формулі
(8) дали криву 2, яка не тільки відрізняється від прямої 1, але
виходить за межі
. Розрахунки по формулі
(8) дали криву 2, яка не тільки відрізняється від прямої 1, але
виходить за межі 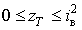 ,
що суперечить фізичному глузду. Дійсно, площини областей а і б
становлять 0,045, тому при
,
що суперечить фізичному глузду. Дійсно, площини областей а і б
становлять 0,045, тому при 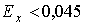 від’ємна область а дає мнимі мінімальні
навантаження
від’ємна область а дає мнимі мінімальні
навантаження 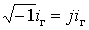 , а
область б - максимальні навантаження, які перевищують
, а
область б - максимальні навантаження, які перевищують  , чого не може бути. І
хоча при
, чого не може бути. І
хоча при 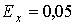 розраховане по ряду максимальне навантаження 0,993
розраховане по ряду максимальне навантаження 0,993 усього на 1,85%
перевищує теоретичне значення 0,975
усього на 1,85%
перевищує теоретичне значення 0,975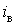 , це не може свідчити на користь можливості
застосування ряду Еджворта, бо з цією ж вірогідністю ряд на 37,1%
занижує мінімальне навантаження (0,141
, це не може свідчити на користь можливості
застосування ряду Еджворта, бо з цією ж вірогідністю ряд на 37,1%
занижує мінімальне навантаження (0,141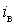 проти теоретичного
значення 0,224
проти теоретичного
значення 0,224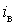 ),
тобто більш, ніж втричі перевищує допустиму
похибку.
),
тобто більш, ніж втричі перевищує допустиму
похибку.Формула (10) при
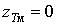 і
і 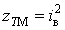 дає криву 3, яка
знаходиться в діапазоні змінення доз. В цьому випадку максимальне і
мінімальне значення становлять
дає криву 3, яка
знаходиться в діапазоні змінення доз. В цьому випадку максимальне і
мінімальне значення становлять 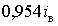 та
та 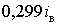 , тобто на -2,15 та 33,5% відрізняються від
теоретичних.
, тобто на -2,15 та 33,5% відрізняються від
теоретичних.