L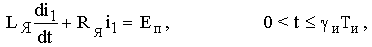 , 0 < t
, 0 < t 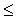
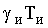 ,
,
(3.1,а)
3. Математические модели систем электропривода постоянного тока с транзисторными ШИП.
3.1. Дискретный датчик ЭДС вращения двигателя постоянного тока
В целом ряде случаев, когда в аналоговых и цифроаналоговых системах электропривода постоянного тока исключена возможность использования в качестве датчиков скорости тахогенераторов, импульсных или других датчиков, выполненных в виде электромеханических устройств и требующих их стыковки с валом исполнительного двигателя, для формирования сигнала обратной связи по скорости вращения наиболее приемлемым является способ, основанный на измерении напряжения на якоре двигателя при периодическом (с периодом
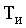 )
обрыве цепи якоря на время (1-
)
обрыве цепи якоря на время (1- )
) [14, 15, 17]. Применение этого способа особенно удобно в
системах электропривода, где двигатель постоянного тока управляется по цепи
якоря от транзисторного широтно-импульсного преобразователя [14 - 17].
Упрощенная функциональная схема устройства, реализующего указанный способ, и
временные диаграммы, иллюстрирующие его работу, приведены соответственно на
рис.3.1,а,б.
[14, 15, 17]. Применение этого способа особенно удобно в
системах электропривода, где двигатель постоянного тока управляется по цепи
якоря от транзисторного широтно-импульсного преобразователя [14 - 17].
Упрощенная функциональная схема устройства, реализующего указанный способ, и
временные диаграммы, иллюстрирующие его работу, приведены соответственно на
рис.3.1,а,б.
Это устройство, называемое измерителем ЭДС вращения (ИЭДС), построено на базе ШИП с силовым транзисторным VT1-VT4 и обратным диодным VД1-VД4 мостами и блоком управления 1 силовыми ключами преобразователя и содержит блоки формирования режима измерения 2 и измерения ЭДС вращения 3. Работа ИЭДС протекает следующим образом.
На интервале времени
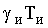 периода измерения
периода измерения 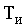 напряжение на якоре ДПТ представляет собой последовательность импульсов
постоянной амплитуды с периодом следования
напряжение на якоре ДПТ представляет собой последовательность импульсов
постоянной амплитуды с периодом следования 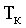 <<
<<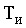 и
относительной длительностью
и
относительной длительностью 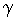 , пропорциональной входному сигналу
ШИП U
, пропорциональной входному сигналу
ШИП U , ток якоря является пульсирующим знакопеременным или
знакопостоянным.
, ток якоря является пульсирующим знакопеременным или
знакопостоянным.
На интервале времени (1-
 )
) периода
периода 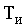 все транзисторы VT1-VT4 силового
моста ШИП заперты сигналом u
все транзисторы VT1-VT4 силового
моста ШИП заперты сигналом u блока 2 и ток якоря падает, замыкаясь
через обратные диоды моста VД1,VД4 (или VД2, VД3) встречно ЭДС Еп
источника питания.
блока 2 и ток якоря падает, замыкаясь
через обратные диоды моста VД1,VД4 (или VД2, VД3) встречно ЭДС Еп
источника питания.
Если ток успевает упасть до нуля к концу интервала времени (1-
 )
) от любых начальных значений вплоть до
пусковых, то напряжение на якоре к концу каждого периода измерения
от любых начальных значений вплоть до
пусковых, то напряжение на якоре к концу каждого периода измерения 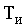 равно
ЭДС вращения ея ДПТ. Зафиксированный в блоке 3 на весь последующий
период измерения (n+1)
равно
ЭДС вращения ея ДПТ. Зафиксированный в блоке 3 на весь последующий
период измерения (n+1) 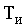 сигнал напряжения на якоре
Uя(nTи) используется в
качестве дискретного сигнала обратной связи по скорости вращения ДПТ w д*.
сигнал напряжения на якоре
Uя(nTи) используется в
качестве дискретного сигнала обратной связи по скорости вращения ДПТ w д*.
Описанный способ формирования сигнала обратной связи позволяет избежать погрешностей в измерении скорости вращения, имеющих место у различного рода тахометрических измерителей и обусловленных нестабильностью параметров цепи якоря ДПТ и токового режима его работы, однако имеет ряд оказывающих существенное влияние на статические и динамические характеристики систем электропривода следующих специфических свойств.
1. Устройство для измерения ЭДС указанным способом не является пассивным по отношению к системе ШИП-ДПТ, оно снижает жесткость ее механических характеристик. Однако, при значениях
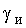 , удовлетворяющих условию
, удовлетворяющих условию 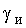
 0,9, жесткость механических
характеристик рассматриваемой системы ШИП-ДПТ с ИЭДС в диапазоне моментов
нагрузок
0,9, жесткость механических
характеристик рассматриваемой системы ШИП-ДПТ с ИЭДС в диапазоне моментов
нагрузок 
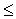 M
M незначительно ниже жесткости соответствующих характеристик обычной системы
ШИП-ДПТ.
незначительно ниже жесткости соответствующих характеристик обычной системы
ШИП-ДПТ.
2. ИЭДС обладает моментной ошибкой, поскольку за время (1-
 )
) , в течение которого силовые
транзисторы ШИП заперты, имеет место уменьшение скорости вращения вала под
действием статического момента нагрузки. Следовательно, сигнал на выходе блока
3, соответствующий значению скорости вращения в конце интервала времени
(1-
, в течение которого силовые
транзисторы ШИП заперты, имеет место уменьшение скорости вращения вала под
действием статического момента нагрузки. Следовательно, сигнал на выходе блока
3, соответствующий значению скорости вращения в конце интервала времени
(1- )
) ,
отличается от среднего за период измерения
,
отличается от среднего за период измерения  значения скорости тем больше, чем выше момент нагрузки.
значения скорости тем больше, чем выше момент нагрузки.
3. Наконец, информация на выходе ИЭДС остается неизменной практически в течение всего периода измерения
 и, следовательно, устройство обладает
динамической ошибкой, зависящей от длительности периода
и, следовательно, устройство обладает
динамической ошибкой, зависящей от длительности периода  .
.
Перечисленные выше свойства ИЭДС необходимо учитывать при проектировании замкнутых систем электропривода. Астатизм в указанных системах обеспечивается путем компенсации моментной ошибки ИЭДС, а быстродействие, ограниченное динамическими ошибками измерителя, может быть увеличено введением в состав системы устройств вычисления мгновенной скорости вращения вала ДПТ, построенных по принципу наблюдающих устройств.
3.2. Пусковые режимы в системе "ШИП-ДПТ-ИЭДС"
3.2.1. Пусковой ток в системе "ШИП-ДПТ-ИЭДС"
Если на интервале времени рабочего состояния ключей
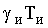 входное напряжение U
входное напряжение U схемы управления СУ составляет
величину U
схемы управления СУ составляет
величину U
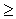 U
U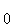 , то транзисторный ШИП находится в
насыщении, относительная продолжительность включения якоря в цепь питания
, то транзисторный ШИП находится в
насыщении, относительная продолжительность включения якоря в цепь питания
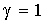 , напряжение на якоре ДПТ постоянно и составляет величину
E
, напряжение на якоре ДПТ постоянно и составляет величину
E . Эквивалентная схема замещения силовой цепи представлена
на рис.3.2.
. Эквивалентная схема замещения силовой цепи представлена
на рис.3.2.
Изменение тока якоря на этом интервале времени характеризуется дифференциальным уравнением
|
L |
(3.1,а) |
его решение имеет вид
|
|
(3.1,б) |
При величине интервала времени
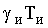
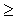 3T
3T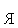 ток
якоря достигает пусковых значений
ток
якоря достигает пусковых значений
|
|
(3.1,в) |
На интервале времени запертого состояния ключей (1-
 )
) ток якоря ДПТ спадает до нуля,
замыкаясь через обратные диоды моста встречно источнику питания Е
ток якоря ДПТ спадает до нуля,
замыкаясь через обратные диоды моста встречно источнику питания Е .
.
Схема замещения силовой цепи для этого интервала представлена на рис.3.3. Изменение тока характеризуется уравнением
|
|
(3.2,а) |
его решение имеет вид
|
|
(3.2,б) |
где
|
|
При

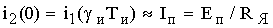 ,
,
и следовательно,
|
|
(3.2в) |
3.2.2. Время спада пускового тока ДПТ до нуля и выбор параметров режима измерения ИЭДС
К моменту окончания интервала времени (1-
 )
) ток якоря ДПТ должен быть равен нулю,
т.е.
ток якоря ДПТ должен быть равен нулю,
т.е. 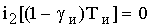 . С учетом выражения (3.2, в) имеем
. С учетом выражения (3.2, в) имеем
|
|
(3.3) |
Выбор величины интервала времени
 запертого состояния ключей ШИП,
гарантирующей спад пускового тока якоря ДПТ до нуля к концу указанного интервала
и нормальное функционирование ИЭДС, и величины периода измерения
запертого состояния ключей ШИП,
гарантирующей спад пускового тока якоря ДПТ до нуля к концу указанного интервала
и нормальное функционирование ИЭДС, и величины периода измерения  следует осуществлять с учетом (3.3) и (3.2) на основании соответственно
соотношений
следует осуществлять с учетом (3.3) и (3.2) на основании соответственно
соотношений
|
|
(3.4,а) |
|
|
(3.4,б) |
при этом величина относительной длительности интервала рабочего состояния ключей ШИП
 определится на основании соотношения
определится на основании соотношения
|
|
(3.4,в) |
В таблице 3.1 приведены значения параметра
 ,
соответствующие различным величинам периода измерения
,
соответствующие различным величинам периода измерения 
Табл.3.1
|
|
3Тя |
4Тя |
5Тя |
8Тя |
10Тя |
|
|
0,77 |
0,82 |
0,86 |
0,91 |
0,93 |
3.2.3. Среднее значение пускового тока и момента системы "ШИП-ДПТ-ИЭДС"
Среднее за период измерения Ти значение пускового тока системы "ШИП- ДПТ-ИЭДС" может быть определено следующим образом
|
|

|
|
(3.5) |
|
= |
Среднее за период измерения Ти значение пускового момента двигателя постоянного тока в рассматриваемой системе может быть определено с учетом (3.5) как
|
|
(3.6) |
В таблице 3.2 приведены значения средних пусковых тока Iср1 и момента Мср1 , соответствующего различным величинам периода измерения Ти
Табл. 3.2
|
|
3Тя |
4Тя |
5Тя |
8Тя |
10Тя |
|
|
0,77 |
0,82 |
0,86 |
0,91 |
0,93 |
|
Iпср1 |
0,57 Iп |
0,65 Iп |
0,72 Iп |
0,82 Iп |
0,86 Iп |
|
Мпср1 |
0,57 Мп |
0,65 Мп |
0,72 Мп |
0,82 Мп |
0,86 Мп |
Анализ полученных результатов показывает, что режим измерения ЭДС вращения приводит к ухудшению энергетических показателей двигателя постоянного тока.
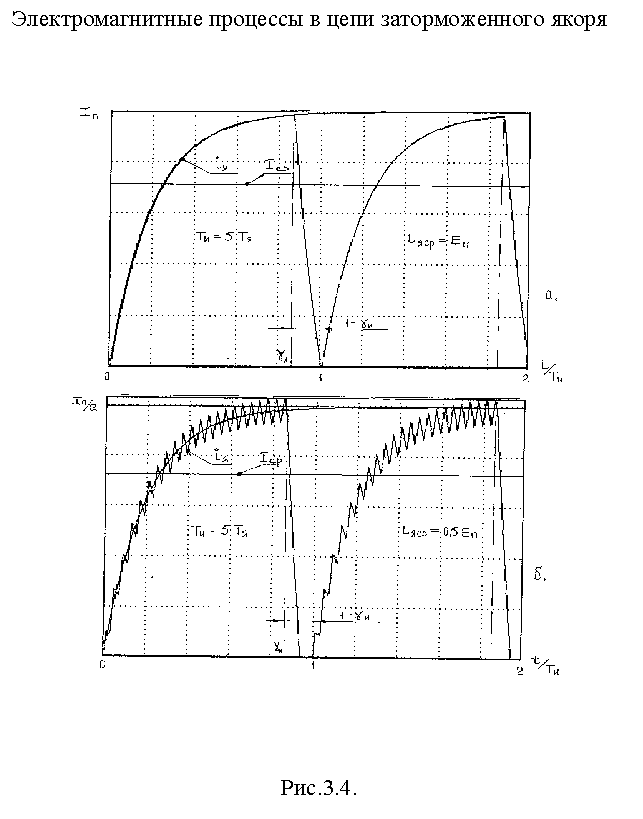
На рис.3.4, а, б представлены процессы в цепи якоря заторможенного двигателя при значении среднего напряжения на якоре соответственно величиной Uяср1 =Еп и Uяср2=0,5Еп
.
3.3. Эквивалентная линейная модель двигателя в режиме измерения ЭДС вращения
Структурная схема системы "ШИП-ДПТ-ИЭДС", представленная на рис.3.5, содержит
ДПТ, ШИП и генератор Г, формирующий режим измерения ЭДС. 
На рис. 3.6, а,б приведены процессы изменения
тока якоря iя и скорости
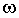 при пуске двигателя в режиме
измерения ЭДС с параметрами Ти=5Тя и Тм
=2Ти соответственно для случаев замкнутой и разорванной связи
по противоЭДС в модели двигателя. Здесь же изображены процессы изменения тока
iяэ и скорости
при пуске двигателя в режиме
измерения ЭДС с параметрами Ти=5Тя и Тм
=2Ти соответственно для случаев замкнутой и разорванной связи
по противоЭДС в модели двигателя. Здесь же изображены процессы изменения тока
iяэ и скорости  э при пуске этого же
двигателя в обычном режиме.
э при пуске этого же
двигателя в обычном режиме.
Наблюдаемое уменьшение быстродействия у двигателя в режиме измерения ЭДС вращения объясняется снижением пускового тока, приводящим к увеличению эквивалентной механической постоянной двигателя.
Определим эквивалентную механическую постоянную двигателя, учитывающую режим измерения ЭДС как
|
|
(3.7) |
где К
1max - коэффициент, учитывающий уменьшение пускового момента двигателя в режиме измерения ЭДС и определяемый на основании (3.5) как|
К 1max=Мпср1/Мп= . . |
(3.8) |
На рис.3.7 представлена эквивалентная линейная модель системы "ШИП-ДПТ" в режиме измерения ЭДС вращения Эта модель содержит ДПТ с эквивалентными механической постоянной Тми1 и электромагнитной постоянной цепи якоря Тяи и усилитель мощности непрерывного типа с коэффициентом передачи на линейном участке статической характеристики Кст =Еп
/ U0 и насыщением выходного сигнала на уровне Еп , наступающим при превышении входным сигналом Uу некоторого напряжения U0 .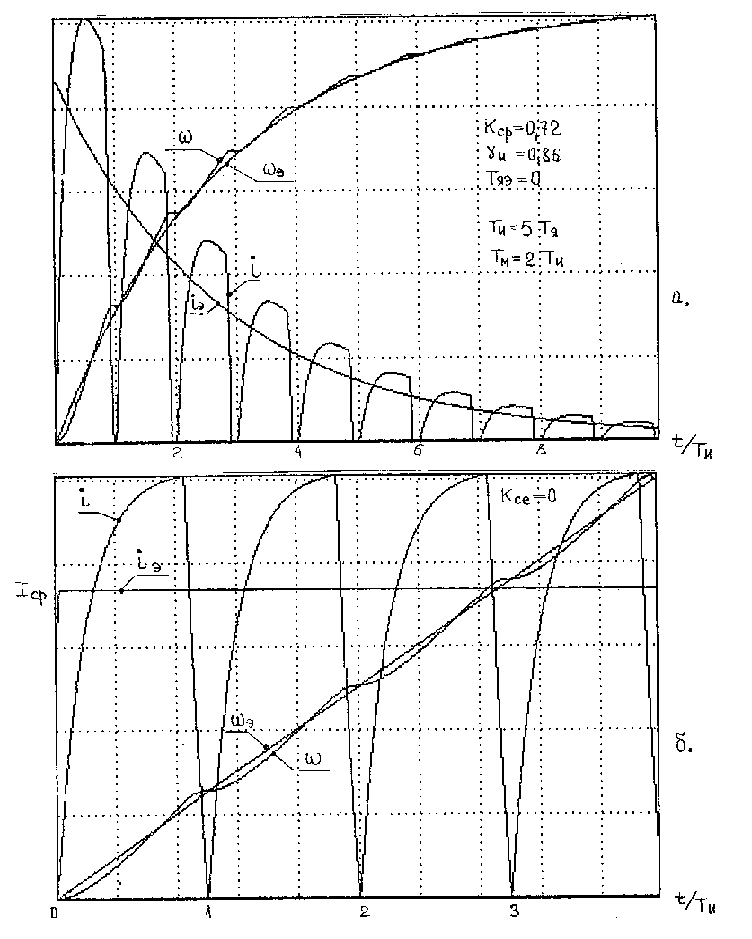
 при пуске двигателя в режиме
измерения ЭДС с параметрами Ти =5Тя , Тм
=2Ти ,
при пуске двигателя в режиме
измерения ЭДС с параметрами Ти =5Тя , Тм
=2Ти , 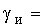 0,86 соответственно для случаев
замкнутой и разомкнутой связи по противоЭДС в модели двигателя. Здесь же
изображены процессы изменения тока iэ и скорости
0,86 соответственно для случаев
замкнутой и разомкнутой связи по противоЭДС в модели двигателя. Здесь же
изображены процессы изменения тока iэ и скорости  в
эквивалентной линейной модели с учитывающими режим измерения ЭДС механической
постоянной Тми =Тм /К1max =Tм/0,72 и электромагнитной постоянной цепи якоря
Тяи , величина которой в модели стремится к нулю, т.к. реальный
пульсирующий пусковой ток якоря в режиме измерения заменен в модели средним
током.
в
эквивалентной линейной модели с учитывающими режим измерения ЭДС механической
постоянной Тми =Тм /К1max =Tм/0,72 и электромагнитной постоянной цепи якоря
Тяи , величина которой в модели стремится к нулю, т.к. реальный
пульсирующий пусковой ток якоря в режиме измерения заменен в модели средним
током.
Анализ представленных процессов показывает весьма удовлетворительное
совпадение переходных процессов по скорости в исследуемой системе "ШИП-ДПТ-ИЭДС"
и поставленной ей в соответствие эквивалентной линейной модели. Процессы пуска
двигателя при относительной продолжительности включения якоря в цепь источника
питания 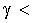 1 представлены на рис. 3.9, а. Там же приведены процессы
в линейной эквивалентной модели с параметрами двигателя, режима измерения ЭДС и
эквивалентной модели , соответствующими рис.3.8.
1 представлены на рис. 3.9, а. Там же приведены процессы
в линейной эквивалентной модели с параметрами двигателя, режима измерения ЭДС и
эквивалентной модели , соответствующими рис.3.8.

Анализ представленных процессов показывает, что нарастание скорости
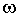 э в эквивалентной линейной модели выше, чем в
реальном двигателе. Указанное отличие объясняется тем, что выбор эквивалентной
механической постоянной Тми1 в эквивалентной модели осуществлялся на
основании соотношения (3.7), учитывающего среднее значение пускового момента.
Среднее за период измерения Ти значение пускового момента при
э в эквивалентной линейной модели выше, чем в
реальном двигателе. Указанное отличие объясняется тем, что выбор эквивалентной
механической постоянной Тми1 в эквивалентной модели осуществлялся на
основании соотношения (3.7), учитывающего среднее значение пускового момента.
Среднее за период измерения Ти значение пускового момента при
 <1 ниже среднего расчетного пускового момента,
определяемого на основании соотношений (3.5) и (3.6) при напряжении на якоре
Uср =
<1 ниже среднего расчетного пускового момента,
определяемого на основании соотношений (3.5) и (3.6) при напряжении на якоре
Uср =  Еп . Это снижение объясняется уменьшением
времени существования тока якоря на интервале времени
Еп . Это снижение объясняется уменьшением
времени существования тока якоря на интервале времени  при
при
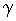 <1, как показано на рис.3.4,б.
<1, как показано на рис.3.4,б.
Как видно, величина эквивалентной механической постоянной Тми переменна и зависит от режима работы двигателя, она минимальна в пусковых режимах и увеличивается с уменьшением тока якоря.
При работе двигателя с номинальным моментом нагрузки время спада номинального тока якоря может быть определено согласно методике п.п.3.2.3. Оно значительно меньше времени спада пускового тока.
Минимальное среднее за период измерения Ти значение тока системы
"ШИП-ДПТ-ИЭДС" при 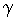 <<1 может быть определено следующим
образом
<<1 может быть определено следующим
образом
|
|
(3.9) |
Максимальное значение эквивалентной механической постоянной рассчитывается как
|
|
(3.10) |
где
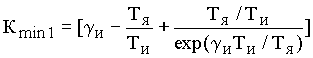 .
.
На рис.3.9, б представлены процессы изменения тока якоря iя и скорости
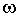 при пуске двигателя с относительной продолжительностью
включения якоря в цепь источника питания
при пуске двигателя с относительной продолжительностью
включения якоря в цепь источника питания 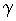 <1 и
процессы в линейной эквивалентной модели при скорректированной на основании
(3.10) и (3.11) величине эквивалентной механической постоянной
<1 и
процессы в линейной эквивалентной модели при скорректированной на основании
(3.10) и (3.11) величине эквивалентной механической постоянной  .
Анализ представленных процессов показывает, что в момент времени t=Ти
скорость двигателя
.
Анализ представленных процессов показывает, что в момент времени t=Ти
скорость двигателя  и эквивалентная скорость
и эквивалентная скорость 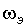 равны.
равны.
В табл.3.3 приведены значения коэффициентов К
max1 и Кmin1, соответствующие различным величинам периода измерения Ти .Табл. 3.3
|
|
3Тя |
4Тя |
5Тя |
8Тя |
10Тя |
|
|
0,77 |
0,82 |
0,86 |
0,91 |
0,93 |
|
К max1 |
0,57 |
0,65 |
0,72 |
0,82 |
0,86 |
|
К min1 |
0,46 |
0,58 |
0,66 |
0,785 |
0,83 |
С учетом Тяи
 0 эквивалентная модель двигателя в
режиме измеренияЭДС может быть представлена структурными схемами, приведенными
на рис.4.10, а,б соответственно при Мс
0 эквивалентная модель двигателя в
режиме измеренияЭДС может быть представлена структурными схемами, приведенными
на рис.4.10, а,б соответственно при Мс 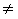 0
и Мс=0.
0
и Мс=0.
3.4. Синтез системы регулирования скорости с дискретным датчиком ЭДС вращения
На рис.3.11 представлена структурная схема одноконтурной системы регулирования скорости ДПТ с дискретным датчиком вращения. Система содержит ДПТ, транзисторный ШИП, генератор Г, формирующий сигналом U1 режим измерения ЭДС вращения, фиксирующий элемент ФЭ, в котором осуществляется под воздействием сигнала U2 генератора Г фиксация ЭДС вращения в дискретные моменты времени nTи и ПИ-регулятор скорости с коэффициентом передачи Крс и временем изодрома Трс
.3.4.1. Линеаризация дискретного датчика ЭДС вращения.
На рис.3.12, а представлены процессы изменения координат электропривода при пуске двигателя в режиме измерения ЭДС с параметрами Ти = 5Тя , Тм = 2Ти
,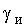 =0,86 с
относительной продолжительностью включения якоря двигателя в цепь источника
питания
=0,86 с
относительной продолжительностью включения якоря двигателя в цепь источника
питания  при разорванной в модели обратной связи по противоЭДС. К
их числу относятся: ток якоря iя и скорость w ; ток iэ и скорость
при разорванной в модели обратной связи по противоЭДС. К
их числу относятся: ток якоря iя и скорость w ; ток iэ и скорость  в
эквивалентной линейной модели при
в
эквивалентной линейной модели при  , Тми =
Тм/Кmax1 =
Тм/0,72;
, Тми =
Тм/Кmax1 =
Тм/0,72; 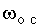 - сигнал на выходе измерителя ЭДС;
f1 - периодический сигнал,
учитывающий пульсации скорости
- сигнал на выходе измерителя ЭДС;
f1 - периодический сигнал,
учитывающий пульсации скорости 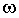 в режиме измерения ЭДС и
удовлетворяющий условию
в режиме измерения ЭДС и
удовлетворяющий условию 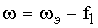 ;
;  - эквивалентная скорость, запаздывающая
относительно
- эквивалентная скорость, запаздывающая
относительно 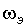 на время
на время 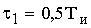 ; f2 - периодический
сигнал, моделирующий работу измерителя ЭДС согласно условию
; f2 - периодический
сигнал, моделирующий работу измерителя ЭДС согласно условию  ,
среднее за период Ти значение которого равно нулю.
,
среднее за период Ти значение которого равно нулю.
С учетом введенных координат
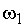 и f2 эквивалентная линейная модель измерителя ЭДС может быть
представлена изображенной на рис.3.13 структурной схемой, содержащей звено
чистого запаздывания с выходным сигналом
и f2 эквивалентная линейная модель измерителя ЭДС может быть
представлена изображенной на рис.3.13 структурной схемой, содержащей звено
чистого запаздывания с выходным сигналом 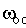 ,
суммируемым далее с сигналом f2.
Суммарный сигнал
,
суммируемым далее с сигналом f2.
Суммарный сигнал 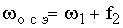 на выходе эквивалентной линейной модели измерителя при
этом равен сигналу
на выходе эквивалентной линейной модели измерителя при
этом равен сигналу  измерителя ЭДС.
измерителя ЭДС.
На рис.3.12, б представлены процессы, аналогичные изображенным на рис.3.12,а, и кроме того:
 - эквивалентная скорость на выходе апериодического звена
первого порядка с постоянной времени
- эквивалентная скорость на выходе апериодического звена
первого порядка с постоянной времени /2, входным сигналом которого является
/2, входным сигналом которого является
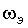 ; f2 - периодический сигнал, моделирующий работу измерителя
ЭДС согласно условию
; f2 - периодический сигнал, моделирующий работу измерителя
ЭДС согласно условию 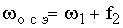 , среднее за период Ти
значение которого в установившемся режиме работы равно нулю.
, среднее за период Ти
значение которого в установившемся режиме работы равно нулю.
С учетом введенных координат
 и f2 эквивалентная линейная модель измерителя ЭДС может быть
представлена изображенной на рис.3.14 структурной схемой, содержащей
апериодическое звено первого порядка с постоянной времени
и f2 эквивалентная линейная модель измерителя ЭДС может быть
представлена изображенной на рис.3.14 структурной схемой, содержащей
апериодическое звено первого порядка с постоянной времени  /2 и
выходным сигналом
/2 и
выходным сигналом  , суммируемым далее с сигналом f2 . Суммарный сигнал
, суммируемым далее с сигналом f2 . Суммарный сигнал 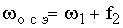 на
выходе эквивалентной линейной модели измерителя при этом равен сигналу
на
выходе эквивалентной линейной модели измерителя при этом равен сигналу
 измерителя ЭДС.
измерителя ЭДС.
3.4.2. Эквивалентная линейная модель системы регулирования скорости с измерителем ЭДС вращения
Эквивалентная линейная модель системы регулирования скорости с ИЭДС с учетом введенных эквивалентных линейных моделей ДПТ в режиме измерения ЭДС и измерителя ЭДС может быть представлена структурной схемой, изображенной на рис. 3.15
Эквивалентная линейная модель измерителя ЭДС в системе представлена апериодическим звеном первого порядка с постоянной времени ТДС и коэффициентом передачи КДС , определяемыми соответственно выражениями (3.12) и (3.13):
|
|
(3.12) |
|
|
(3.13) |
где Кфэ
= Uосмах /Еп и Uосмах - соответственно коэффициент передачи фиксирующего элемента ФЭ и максимальное значение сигнала на его выходе.Последняя структурная схема при Тяи  0 и при
отсутствии сигнала помехи f2 может быть приведена к виду, показанному на рис.3.16.
0 и при
отсутствии сигнала помехи f2 может быть приведена к виду, показанному на рис.3.16.
При выборе времени изодрома регулятора скорости на основании соотношения
|
Трс=Тми=Тм/К 1, |
(3.14) |
передаточная функция замкнутой системы приводится к виду
|
|
(3.15) |
Анализ полученной передаточной функции показывает, что в рассматриваемой эквивалентной системе может быть осуществлена настройка на "оптимум по модулю" в случае выбора коэффициента передачи ПИ-регулятора Крс на основании соотношения
|
|
(3.16) |
и установке на входе системы сглаживающего фильтра с постоянной времени
|
Тф=Тдс=Ти /2, |
(3.17) |
При этом передаточная функция замкнутой системы приобретает вид
|
|
где
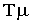 = Тдс = Ти /2.
= Тдс = Ти /2.
Если принять амплитуду опорного напряжения ШИП U
0 и величину максимального сигнала на выходе фиксирующего элемента U0max равными 10 В, то статический коэффициент передачи ШИП Кст , коэффициент передачи ФЭ К фэ и эквивалентный коэффициент передачи датчика скорости Кдс могут быть рассчитаны по формулам соответственно|
Кст = Еп / 10, |
(3.18) |
|
Кфэ = 10/Eп , |
(3.19) |
|
Кдс = 10/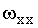 . . |
(3.20) |
Тогда выражение (3.16) приводится к виду
|
|
(3.21) |
На рис. 3.17 представлена структурная схема одноконтурной системы регулирования скорости с измерителем ЭДС и входным сглаживающим фильтром
. На рис. 3.18, а представлены кривые, характеризующие переходные процессы по скорости ( ,
, 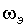 ) и
току якоря ( iя , iэ)
при реакции системы на скачек задающего воздействия для случаев Тф
) и
току якоря ( iя , iэ)
при реакции системы на скачек задающего воздействия для случаев Тф
 0. Параметров регуляторов Крс и Трс
в исследуемой системе с измерителем ЭДС получены на основании расчета
эквивалентной системы по соотношениям (3.17-3.21). Величина коэффициента
К1 , учитывающего режим
измерения, была при расчете системы принята минимальной, т.е. К1
= К1min .
0. Параметров регуляторов Крс и Трс
в исследуемой системе с измерителем ЭДС получены на основании расчета
эквивалентной системы по соотношениям (3.17-3.21). Величина коэффициента
К1 , учитывающего режим
измерения, была при расчете системы принята минимальной, т.е. К1
= К1min .
Сравнительный анализ показывает достаточно хорошее приближение процессов в реальной системе с измерителем ЭДС к процессам в эквивалентной линейной системе.
В табл.3.4 приведены параметры переходных процессов в исследуемой системе и эквивалентной ей линейной системе при Тф
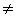 0.
0.
Табл. 3.4.
|
Настройка на "оптимум по модулю", Тф 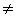 0 0 | |||
|
Система |
Время первого сог- ласования, t p1/Ти |
Время входа в зону
|
Перерегул.
|
|
Эквивал. |
2,4 |
4,8 |
4,7 |
|
Исслед. |
2,8 |
2,7 |
1,5 |
На рис.3.18, б представлены переходные процессы по скорости
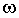 и току
якоря iя при отработке исследуемой системой скачка задающего
воздействия для Тф = 0. Как
видно, переходный процесс в исследуемой системе заканчивается за один период
измерения Ти .
и току
якоря iя при отработке исследуемой системой скачка задающего
воздействия для Тф = 0. Как
видно, переходный процесс в исследуемой системе заканчивается за один период
измерения Ти .
Сигнал обратной связи
 на выходе фиксирующего элемента ФЭ в
момент времени t=Ти при Трс и Крс ,
рассчитанных по формулам соответственно (3.14) и (3.21), можно с учетом (3.18)и
(3.20) определяется выражением
на выходе фиксирующего элемента ФЭ в
момент времени t=Ти при Трс и Крс ,
рассчитанных по формулам соответственно (3.14) и (3.21), можно с учетом (3.18)и
(3.20) определяется выражением
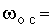
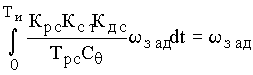 .
.
В эквивалентной линейной модели системы, структурная схема которой представлена на рис.3.16, может быть обеспечена настройка на "симметричный оптимум".
С учетом соотношений (3.18)-(3.20), определяющих статический коэффициент передачи ШИП Кст , коэффициент
передачи ФЭ Кфэ и эквивалентный коэффициент передачи датчика скорости Кдс передаточная функция замкнутой системы может быть представлена следующим выражением|
|
(3.22) |
Введем обозначения
|
Трс Тми Тдс/Крс =8 , , |
(3.23а) |
|
Трс (Тми Тдс)/Крс =8 , , |
(3.23б) |
|
Трс (1+1/Крс ) =4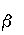 . . |
(3.23в) |
Из соотношения (3.23в) находим
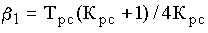 .
.
Разделив (3.23б) на (3.23в) и (3.23а) на (3.23б), получим соответственно
 ,
, 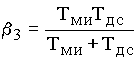 .
.
Полагая
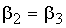 , определяем коэффициент Крс :как
, определяем коэффициент Крс :как
|
|
(3.24,а) |
Из условия
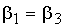 с учетом (3.24а) определяем коэффициент Трс
:
с учетом (3.24а) определяем коэффициент Трс
:
|
|
(3.24,б) |
После подстановки соотношений (3.24,а) и (3.24, б) в выражение (3.22) получаем передаточную функцию замкнутой системы, настроенной на "симметричный оптимум" в виде
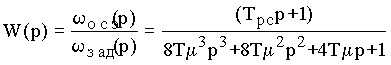 ,
,
где Т
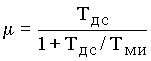 .
.
При Тми >>Тдс выражения (3.24, а) и (3.24, б) могут быть заменены на приближенные:
|
|
(3.25,а) |
|
|
(3.25,б) |
На рис.3.19,а представлены переходные процессы по скорости (
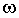 ,
,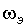 ) и току якоря (iя
,iэ )в настроенной на
"симметричный оптимум" системе при отработке скачка задающего воздействия для
случая Тф =0. Величины параметров регуляторов Крс и
Трс в исследуемой системе с измерителем ЭДС получены на основании
расчета эквивалентной линейной системы по соотношениям (3.25, а), (3.25, б) и
(3.18)-(3.20), причем величина коэффициента К1, учитывающего режим измерения, выбиралась минимальной,
т.е. К1 ==К1min
.
) и току якоря (iя
,iэ )в настроенной на
"симметричный оптимум" системе при отработке скачка задающего воздействия для
случая Тф =0. Величины параметров регуляторов Крс и
Трс в исследуемой системе с измерителем ЭДС получены на основании
расчета эквивалентной линейной системы по соотношениям (3.25, а), (3.25, б) и
(3.18)-(3.20), причем величина коэффициента К1, учитывающего режим измерения, выбиралась минимальной,
т.е. К1 ==К1min
.
Для уменьшения перерегулирования на входе системы необходима установка сглаживающего фильтра с постоянной времени Тф , определяемой на основании соотношения
|
Тф = Трс |
(3.26) |
На рис.3.19, б представлены переходные процессы в настроенной на "симметричный оптимум" системе при отработке скачка задающего воздействия для случая Тф
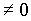 .
.
ЗАКЛЮЧЕНИЕ
Основные результаты проекта, такие как: программно-аппаратный комплекс микропроцессорного управления и интерактивного интерфейса ввода, вывода для систем управления и снятия необходимых характеристик исследуемых электроприводов, требования к составу оборудования, варианты индивидуальных домашних заданий для расчета и моделирования процессов в исследуемых системах из условия возможности экспериментальной проверки результатов на стенде, методические
указания к выполнению цикла работ на каждом лабораторном стенде, включающие основы теории, описание лабораторной установки, программы работ, методики снятия статических и динамических характеристик, опросные тесты и т.п.; позволят перевести процесс создания лабораторного оборудования начала XXI века в практическую плоскость. Особую перспективу результаты данного проекта будут иметь при создании лабораторного оборудования для высших и средних учебных заведений электромеханического и приборостроительного профиля. Создание макетного головного стенда вентильного электропривода на основе двигателя постоянного тока, содержащего исследуемую и нагрузочную электромашины и PC IBM, позволит внедрить и использовать в учебном процессе перспективную технологию на уровне мировых стандартов.Результаты работ по данному проекту могут быть использованы при создании прецизионных электроприводов опорно-поворотных устройств различного назначения (оптотехника, робототехника, полиграфия, станкостроение и т.д.).
Разработанный лабораторный комплекс по существу альтернативных вариантов не имеет и при стоимости одного стенда (включая стоимость ПЭВМ) порядка 9 000 у.е. - 9 500 у.е. вполне конкурентноспособен.
К работе над данным проектом кроме профессорско-преподавательского состава кафедры ЭТ и ПЭМС привлекались сотрудники проблемной лаборатории, аспиранты и студенты старших курсов, обучающихся по направлению 654500 "Электротехника, электромеханика и электротехнологии".
В дальнейшем необходимо разработать и создать по такой же технологии остальные стенды рассматриваемого лабораторного комплекса.
Список литературы
14. Кротенко В.В., Синицын В.А., Толмачев В.А., Томасов В.С. Бестахогенераторный
электропривод постоянного тока. // Серия "Механизация и автоматизация производственных
процессов. Л. ЛДНТП, 1987.
15. Кротенко В.В., Синицын В.А., Толмачев В.А., Томасов В.С. Система ШИП-ДПТ с устройством
измерения ЭДС вращения. // В кн. "Электромашиностроение и электрооборудование",
Техника, Киев, вып.41, 1987.
16. Игнатченко А.И., Кротенко В.В., Толмачев В.А. Широкополосные системы электропривода с
широтно-импульсными преобразователями и дискретными датчиками координат.
//Электротехника, 1988, №5.
17. Кротенко В.В., Синицын В.А., Толмачев В.А., Томасов В.С. Дискретный датчик ЭДС
вращения двигателя постоянного тока. // В сб. "Микропроцессорное управление в системах
энергообеспечения и электропривода". Томск, 1991.
| ДонНТУ | Автобиография | | Реферат | | Перечень ссылок | | Отчет о поиске | Туризм | |
| Портал магистров ДонНТУ |