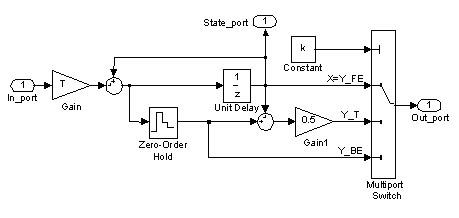
Рисунок 1 – Розгорнута модель дискретного інтегратора з різними алгоритмами чисельного інтегрування
Робота була представлена на науково-практичній студентській конференції
«Сучасні проблеми електромеханічних систем автоматизації та електроприводу»
Дніпродзержинський державний технічний університет 21-24 травня 2007 року.
В останній час спеціалісти в області автоматичного керування електромеханічними об‘єктами все частіше використовують для синтезу та аналізу систем пакет MATLAB з його поширеннями Simulink і Control Toolbox. Прагнення авторів цього програмного продукту до розширення його можливостей та підвищення універсальності привело до того, що при реконструкції деяких Simulink-блоків та m-функцій під час розробки нових MATLAB-версій вони стали занадто складними і в деяких режимах, або при деяких параметрах можуть працювати неадекватно. Отже, метою роботи є виявлення слабких місць в інструментах моделювання та аналізу дискретних систем в середовищі пакету MATLAB і розробка рекомендацій щодо подолання виявлених недоліків.
Одним з основним блоків бібліотеки Discrete програми структурного моделювання Simulink є Discrete-Time Integrator [1-5]. Він може, за вибором користувача, застосовувати один із трьох методів чисельного інтегрування (Integrator method): Forward Euler, Backward Euler і Trapeziodal.
Один крок чисельного інтегрування (ЧІ) переліченими методами описується різницевими рівняннями
YFE(nT)=YFE(nT-T)+Tu(nT-T), (1.1)
YBE(nT)=YBE(nT-T)+Tu(nT) , (1.2)
YT(nT)=YT(nT-T)+T[u(nT-T)+u(nT)]/2 , (1.3)
яким відповідають дискретні передавальні функції
WFE(z)=YFE(z)/u(z)=T/(z-1) , (1.4)
WBE(z)=YBE(z)/u(z)=T*z/(z-1) , (1.5)
WT(z)=YT(z)/u(z)=T*(z+1)/[2*(z-1)] . (1.6)
Застосування різних методів ЧІ можна продемонструвати за допомогою деталізованої моделі, зображеної на рис. 1, і перехідних функцій, приведених на рис. 2.
Як видно з рис. 1, основу цифрового інтегратора складає ланка запізнювання на період дискретності Unit Delay, замкнена додатним зворотним зв'язком. Блок Zero-Order Hold (Екстраполятор Нульового Порядку) узгоджує між собою вихідні сигнали аналогових та дискретних блоків. Один від одного інтегратори з різними алгоритмами ЧІ відрізняються точкою знімання вихідного сигналу. Вибір методу ЧІ здійснюється присвоюванням параметру k блоку Constant одного з цілочисельних значень (1, 2, 3), яке визначає номер входу блоку Multiport Switch, що з‘єднується з його виходом.

Рисунок 1 – Розгорнута модель дискретного інтегратора
з різними алгоритмами чисельного інтегрування
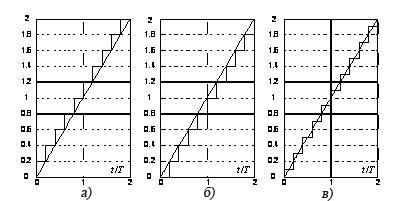
Рисунок 2 – Перехідні функції дискретних інтеграторів з різними
методами чисельного інтегрування:
а) Backward Euler, б) Forward Euler, в) Trapeziodal
До версії MATLAB-4х мав три дискретних інтегратора: звичайний, з обмеженням вихідного сигналу (Limited) та зі скиданням вихідного сигналу при виконанні заданої умови у початковий стан (Reset). У більш пізніх версіях ці три блоки об‘єднані в один, режими роботи якого визначаються у вікні введення параметрів, показаному на рис. 3.

Рисунок 3 – Вікно визначення параметрів блоку Discrete-Time Integrator
Ускладнення алгоритму роботи дискретного інтегратора призвело до деяких похибок в його роботі. Зокрема, при встановленні на вході цього блоку ланки Constant (Константа) або ланки Step (Сходинка) з нульовим значенням параметру Step time перехідні функції інтегратора не змінюються при зміні методу чисельного інтегрування і мають вигляд рис. 2а. Так само веде себе дискретний інтегратор і при використанні його порту стану для розв‘язання алгебраїчного контуру. Отже, в таких випадках краще використовувати не бібліотечний блок, а створити його власноруч за схемою рис. 1. Для обмеження вихідних сигналів дискретних інтеграторів у моделі рис. 1 треба блок Unit Delay замінити блоком запізнювання з обмеженням вихідного сигналу, який можна створити за допомогою моделі рис. 4 на виходах блоків Zero-Order Hold та Gain1 установити ланки Saturation (Обмеження Координат) з тими ж самими рівнями обмеження, що задані в блоках Constant і Constant1 моделі рис. 4.
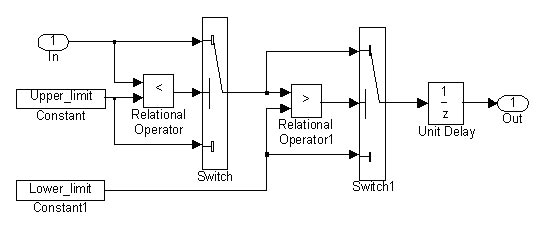
Рисунок 4 – Модель блоку запізнення на період дискретності
з обмеженням вихідного сигналу
У перемикачах Switch і Switch1 моделі рис. 4 значення параметру Threshold повинно задовольняти умові . Зазвичай приймають середнє значення указаного діапазону, тобто .
У перемикачах Switch і Switch1 моделі рис. 4 значення uT параметру Threshold повинно задовольняти умові uT більше 0, та менше 1 . Зазвичай приймають середнє значення указаного діапазону, тобто uT=0.5 .
1. Блок Discrete-Time Integrator моделюючої програми Simulink в деяких режимах виконує чисельне інтегрування не заданим методом, а методом Forward Euler. Позбавитися цього недоліку можна застосуванням запропонованої в роботі моделі рис.1
2. Для обмеження вихідних сигналів дискретних інтеграторів їх передавальні функції необхідно деталізувати та замінити блоки запізнювання на період дискретності такими ж блоками з обмеженням, виконаними за структурою рис. 4.
[Библиотека]