перевод с английского Гузь А. Г.

Источник: www.pmarneffei.hku.hk/mbetoolbox/matlab_doc/toolbox/powersys/synchronousmachine.html

Синхронная машина

      Цель: Моделирование динамических процессов в трехфазной неявнополюсной и явнополюсной синхронной машине.

Описание

      Блок «Синхронная машина» работает в генераторном или двигательном режимах. Режим работы зависит от знака механической энергии (положительный – для генераторного, отрицательный – для двигательного). Электрическая часть машины представлена моделью с шестью пространствами состояния, а механическая часть – такая же, как в блоке «Упрощенная синхронная машина».
      Модель учитывает динамические свойства статорной, демпферной обмоток и обмотки возбуждения. Эквивалентная цепь модели представлена в системе координат ротора (dq-система). Все параметры ротора и электрические величины рассматриваются относительно статора. Они определены первичными переменными. Приняты следующие обозначения:
      • d, q : величины по осям d и q
      • R, s : роторная и статорная величина
      • l, m : индуктивности рассеяния и намагничивания
      • f, k : величины относящиеся к обмотке возбуждения и демпферной обмотке
      Электрическая цепь машины представлена на рисунке:

      со следующими уравнениями:

Диалоговое окно и параметры

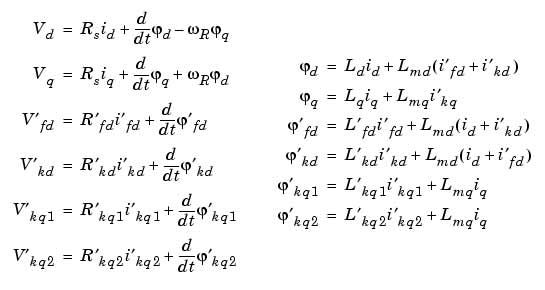
       В библиотеке Powerlib можно выбрать один из трех блоков «Синхронная машина», чтобы определить параметры модели.

Оcновные параметры в системе СИ

Тип ротора

       Определяет тип ротора: явнополюсный или неявнополюсный (цилиндрический). Этот выбор определяет число роторных обмоток на оси q (демпферные обмотки).

Номинальные параметры

       Полная допустимая трехфазная мощность Рн (ВА), действующее значение линейного напряжения Uн(В), частота f(Гц) и ток возбуждения Iвн (А).
       Номинальный ток возбуждения - ток, который производит номинальное напряжение без нагрузки. Эта модель была разработана со всеми величинами, приведенными к статору, Номинальный ток возбуждения дает возможность вычислить коэффициент приведения машины, который позволяет применить напряжение возбуждения, приведенное к ротору, как в действительности. Это также позволяет представить ток возбуждения, который является одной из переменных в выходном векторе, относительно ротора. Если величина номинального тока возбуждения неизвестна, вы должны задать 0. Т.к. коэффициент приведения вычислить нельзя в этом случае, вы должны принять напряжение возбуждения приведенное к статору и ток возбуждения в выходном векторе также будет приведен к статору.

Статор

       Сопротивление Rs (Ом), индуктивность рассеяния Lls (Гн), и индуктивности намагничивания по осям d и q Lmd (Гн) и Lmq (Гн).

Oбмотка возбуждения

      Сопротивление возбуждения Rf ’ (Ом) и индуктивность рассеяния Llfd’ (Гн), оба приведенные к статору.

Демпферные обмотки

      Сопротивление по оси d Rkd’ (Ом) и индуктивность рассеяния L1kd’ (Гн), сопротивление по оси q Rkq1’ (Ом) и индуктивность рассеяния L1kq’ (Гн), и (только если цилиндрический ротор) сопротивление по оси q Rkq2’(Ом) и индуктивность рассеяния L1kq2’ (Гн). Все эти значения приведены к статору.

Механические параметры

      Коэффициент инерции J (кг*м2), коэффициент демпфирования D (Нм*с/рад), и число пар полюсов р.

Начальные условия

       Начальное отклонение скорости dw (% от номинальной скорости), электрический угол ротора Oе (град), амплитуды линейных токов, iA, iB, iC (А) и фазные углы (phiA, phiB, phiC (град), и начальное напряжение возбуждения Vf(В). Вы можете определить начальное напряжение возбуждения двумя способами. Если вы знаете номинальный ток возбуждения (первая строка, последний параметр) введите в диалоговое окно начальное напряжение возбуждения в вольтах относительно ротора. Иначе, введите 0 вместо номинального тока возбуждения, как объяснено ранее, и определите, начальное напряжение возбуждения в вольтах относительно статора. Номинальное напряжение возбуждения приведенное к статору может быть легко определено отметив внизу диалогового окна строку Displау Vfd which produces a nominal Vt.

Учет насыщения

      Определяем будет ли учтено при моделировании явление магнитного насыщения статорного и роторного магнитопроводов или нет.

Насыщение

      Параметры кривой насыщения в режиме холостого хода. Магнитное насыщение статорного и роторного магнитопроводов моделируются нелинейной функцией, в этом случае полиномом, используя точки кривой намагничивания холостого хода. Вы должны задать матрицу размером 2*n,где n – число точек взятых из кривой намагничивания. Первый ряд этой матрицы содержит значения токов возбуждения, в то время как второй – приложенные напряжения.

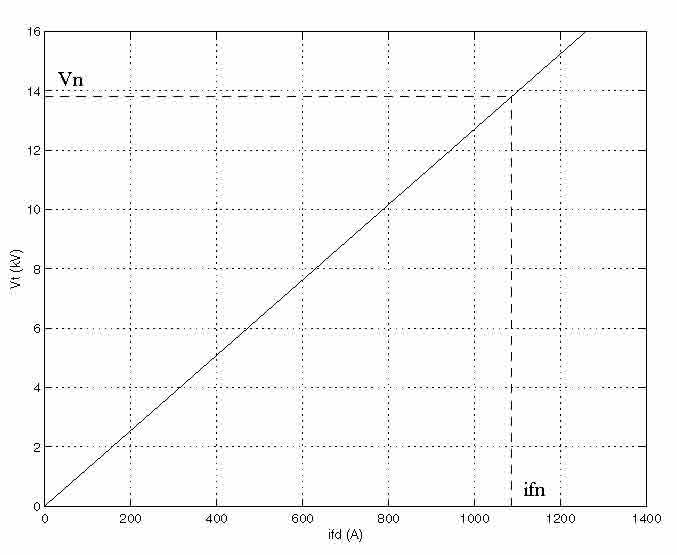
      Первая точка (первый столбец матрицы) должна соответствовать точке в которой начинается эффект насыщения. Вы должны отметить поле Simulate saturation для симуляции насыщения. Эта отметка разрешает вам ввести матрицу параметров для симуляции насыщения. Если Вы не хотите моделировать насыщение, просто не отмечайте поле Simulate saturation. В этом случае зависимость между ifd и Vf становится линейной (без насыщения).

      В качестве примера, без насыщения, может быть приведена типичная кривая. Здесь ifn= 1087 (А), а Vn= 13800 (В) действующее линейное напряжение, которому также соответствует фазное напряжение 11268 В.

       Когда насыщение моделируется, полином соответствует кривой, соответствующей матрице точек, которую вы вводите. Чем больше точек вы вводите, тем лучше соответствие оригинальной кривой.

       Следующий рисунок иллюстрирует это графически (ромбы – это реальные точки введенные в диалоговом окне.)

B данном случае были использованы следующие значения :
       • ifn = 1087 A
       • ifd= [695.64, 774.7, 917.5, 1001.6, 1082.2, 1175.9, 1293.6, 1430.2, 1583.7] A
       • Vt = [9660,10623,12243,13063,13757,14437,15180, 15890, 16567] В

[Библиотека]