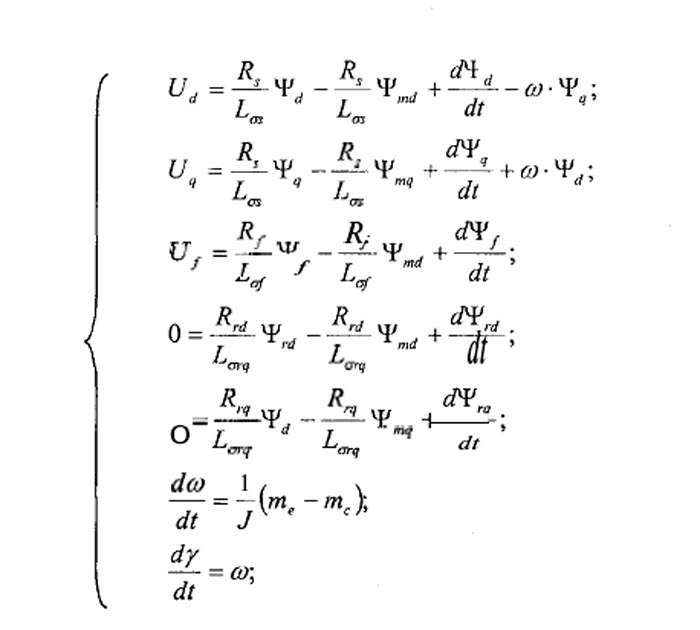
Область применения регулируемых электроприводов переменного тока в нашей стране и за рубежом в значительной степени расширяется. Особое положение занимает синхронный электропривод мощных карьерных экскаваторов, которые используются для компенсации реактивной мощности. Однако их компенсирующая способность используется недостаточно из-за отсутствия чётких рекомендаций по режимам возбуждения.

Соловьев Д. Б.

      Область применения регулируемых электроприводов переменного тока в нашей стране и за рубежом в значительной степени расширяется. Особое положение занимает синхронный электропривод мощных карьерных экскаваторов, которые используются для компенсации реактивной мощности. Однако их компенсирующая способность используется недостаточно из-за отсутствия чётких рекомендаций по режимам возбуждения. В этой связи ставиться задача определения наивыгоднейших режимов возбуждения синхронных двигателей с точки зрения компенсации реактивной мощности с учётом возможности регулирования напряжения. Эффективное использование компенсирующей способности синхронного двигателя зависит от большого количества факторов (технических параметров двигателя, нагрузки на валу, напряжения на зажимах, потерь активной мощности на выработку реактивной и т.д.). Увеличение загрузки синхронного двигателя по реактивной мощности обуславливает рост потерь в двигателе, что отрицательно сказывается на показателях его работы. В то же время увеличение реактивной мощности, отдаваемой синхронным двигателем, будет способствовать уменьшению потерь энергии и в системе электроснабжения карьера [1]. По этому критерием оптимальности нагрузки синхронного двигателя по реактивной мощности является минимум приведенных затрат на генерацию и распределение реактивной мощности в системе электроснабжения карьера.

      Исследование режима возбуждения синхронного двигателя не посредственно на карьере, не всегда представляется возможным по техническим причинам и из-за ограниченного финансирования исследовательских работ. Поэтому представляется необходимым описание синхронного двигателя экскаватора различными математическими методами. Двигатель, как объект автоматического управления представляет собой сложную динамическую структуру, описываемую системой нелинейных дифференциальных уравнений высокого порядка. В задачах управления любой синхронной машиной использовали упрощенные линеаризованные варианты динамических моделей, которые давали лишь приближённое представление о поведении машины. Разработка математического описания электромагнитных и электромеханических процессов в синхронном электроприводе, учитывающих реальный характер нелинейных процессов в синхронном электродвигателе, а также использование такой структуры математического описания при разработки регулируемых синхронных электроприводов, при которой исследование модели карьерного экскаватора было бы удобным и наглядным, представляется актуальной.

       Вопросу моделирования всегда уделялось большое внимание, широко известны методы: аналог моделирования, создания физической модели, цифро-аналогово моделирования. Однако аналоговое моделирование ограничено точностью вычислений и стоимостью набираемых элементов. Физическая модель наиболее точно описывает поведение реального объекта. Но физическая модель не позволяет произвести изменение параметров модели и создание самой модели очень дорого.

       Наиболее эффективным решением является система проведения математических расчётов MatLAB, пакета SimuLink. Система MatLAB устраняет все недостатки вышеперечисленных методов. В данной системе уже сделана программная реализация математической модели синхронной машины.

       Среда разработки лабораторных виртуальных приборов MatLAB представляет собой среду прикладного графического программирования, используемую в качестве стандартного инструмента для моделирования объектов, анализа их поведения и последующего управления. Ниже приведён пример уравнений для моделируется синхронного двигателя по полным уравнениям Парка-Горева, записанным в потокосцеплениях для схемы замещения с одним демпферным контуром.

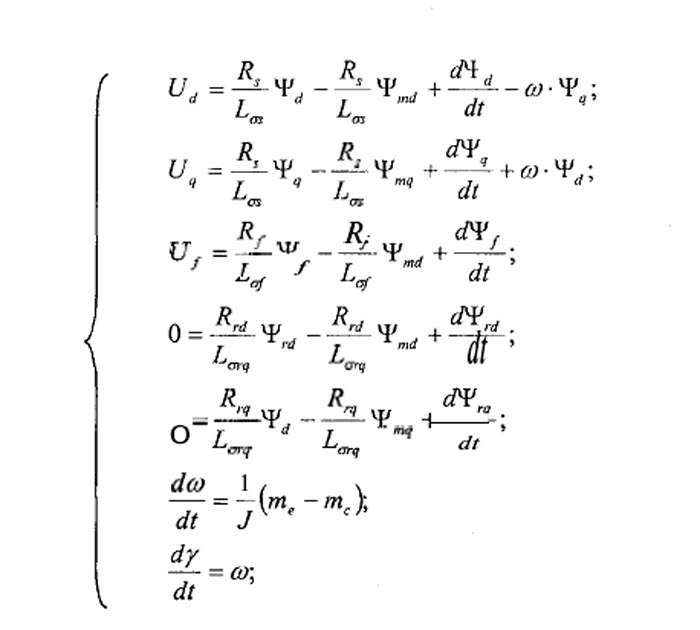
       С помощью данного программного обеспечения можно моделировать все возможные процессы в синхронном двигателе, в штатных ситуациях. На рис. 1 показаны режимы пуска синхронного двигателя, получившиеся при решении уравнения Парка-Горева для синхронной машины.

       Пример реализации этих уравнений представлен на блок-диаграмме, где инициализируются переменные, устанавливаются параметры и выполняется интегрирование. Результаты режима пуска приведены на виртуальном осциллографе.

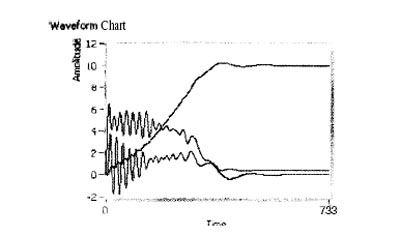
       Рис. 1 Пример снятых характеристик с виртуального осциллографа.

       Как видно, при пуске СД возникают ударный момент величиной 4.0 о.е и ток 6.5 о.е. Время пуска составляет порядка 0.4 сек. Хорошо видны колебания тока и момента, вызванные не симметрией ротора.

       Однако использование данных готовых моделей делает затруднительным исследование промежуточных параметров режимов синхронной машины из-за невозможности изменения параметров схемы готовой модели, невозможности изменения структуры и параметров сети и системы возбуждения, отличных от принятых, одновременного рассмотрения генераторного и двигательного режима, что необходимо при моделировании пуска или при сбросе нагрузки. Кроме того, в готовых моделях применен примитивный учёт насыщения - не учтено насыщение по оси "q". В то же время в связи с расширением области применения синхронного двигателя и повышением требований к их эксплуатации требуются уточнённые модели. То есть, если не обходимо получить конкретное поведение модели (смоделированного синхронного двигателя), в зависимости от горно-геологических и других факторов влияющих на работу экскаватора, то необходимо дать решение системы уравнений Парка-Горева в пакете MatLAB, позволяющее устранить указанные недостатки.

ЛИТЕРАТУРА

1. Кигель Г. А., Трифонов В. Д., Чирва В. X. Оптимизация режимов возбуждения синхронных двигателей на железорудных горно-обогатительных предприятиях.- Горный журнал, 1981 г, Ns7, с. 107-110.

2. Норенков И. П. Автоматизированное проектирование. - М.: Недра, 2000, 188 стр.



[Библиотека]