Кадуба Л.М., Рай А.В.

Материалы Всеукраинской научно-технической конференции студентов «Электротехника, электроника и микропроцессорная техника», г. Донецк, 28 – 29 мая 2008 г.

Ефективність використання теорії ймовірностей у електроенергетиці, як і в інших галузях науки й техніки, обумовлена принципом практичної впевненості (ППВ), згідно з яким у розрахунках враховується не весь діапазон можливих значень параметра режиму, а тільки діапазон R практично достовірних (рис. 1).

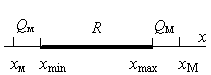
     Рисунок 1

Елементи системи електропостачання вибираються за розрахунковим діапазоном (х_min, x_max), який менше можливого діапазону (x_м, х_М), чим зменшуються капітальні витрати.

Граничні ймовірності E_min, E_max появи випадкової величини в діапазонах Q_м малих і Q_М великих значень зв’язані з імовірністю E_R практично достовірних подій співвідношенням:

(1)

У літературі ППВ викладається стосовно до необмежених випадкових величин, однак при цьому відсутній єдиний підхід до реалізації ППВ: до однієї випадкової величини застосовується завдання граничних ймовірностей, а для двох величин – однакова щільність розподілу. Умовно перший спосіб назвемо «граничним», а другий – «рівної щільності» (знак ~ у позначеннях). Зіставлення цих способів і можливість їх застосування до обмежених випадкових величин, що часто зустрічаються у практичних додатках, не розглядалися. У стандарті [1] для всіх показників електромагнітної сумісності (ЕМС) у нормальному режимі прийняте єдине значення інтегральної імовірності E_i = 0,95. Для однобічних показників (коефіцієнти несиметрії, несинусоїдальності та ін.) такий підхід є повністю виправданим, оскільки тут не потрібне визначення мінімальних значень. Тоді при E_R = E_i перевищення максимальних значень допускається з гранич-ною ймовірністю E_xmax=1 - E_i=0.05. Однак для «діапазонних» показників (відхилення напруги і частоти) завдання тільки інтегральної імовірності недостатньо. Дійсно, якщо, як і попередньому випадку, трактувати її як E_R = 0,95, то згідно з (1) буде відома лише сума граничних ймовірностей, але не самі ймовірності.

Мета даної роботи полягає в обґрунтуванні способу реалізації ППВ й усуненні невизначеності при виборі граничних ймовірностей.

Розглянемо спосіб рівної щільності. У цьому випадку для реалізації ППВ потрібно знання ймовірності Геометрично для однієї випадкової величини х точки рівної щільності дають горизонталь на графіку щільності розподілу f(x) .На рис 2,а показана крива щільності нормального розподілу, яку горизонталь 1 перетинає в двох точках. Для того, щоб абсциси цих точок були шуканими розрахунковими значеннями, горизо-нталь необхідно підіймати доти доки площа фігури з основою x_max – х_min не стане рівною Якщо спосіб використовується до обмеженої випадкової величини з рівномірною щільністю (рис. 2,б), то ні у якому разі неможливо добитися, щоб площа дорівнювалa оскільки при любому положенні горизонталі 1 площе дорівнюватиме одиниці. При цьому для показників ЕМС будь-якого виду «розрахунковим» виявляється весь діапазон можливих значень, що суперечить ППВ.

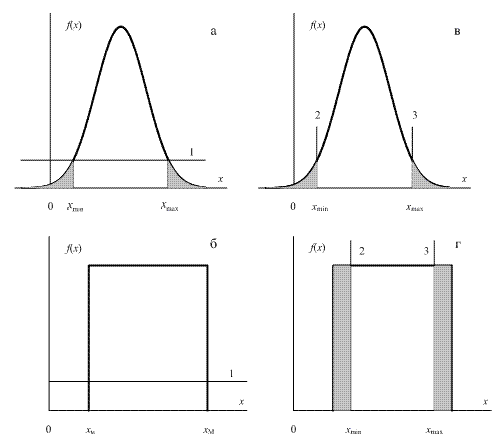
     Рисунок 2

Вихідними для граничного способу є граничні ймовірності. Геометрично спосіб реалізується шляхом переміщення двох вертикалей до тих пір, доки площа фігури, що відтинається від кривої щільності ліворуч від вертикалі 2 (рис. 2,в-г) не стане рівною E_xmin, а праворуч від вертикалі 3 – величині E_xmax. Легко бачити, що цей спосіб є коректним у всіх випадках.

Для симетричних кривих розподілів і при однакових граничних ймовірностях E_x обидва способи дають однакові результати. Чим більше асиметрія й обмеження, тим більшими будуть розходження.

Опит ймовірнісних розрахунків у різних галузях науки й техніки показує, що граничні ймовірності можна приймати у межах від 0,05 до 0,001. Для показників ЕМС [1] прийнята інтегральна ймовірність 0,95, якій відповідає гранична імовірність E_x = 0,05. Її слід приймати для двобічних показників ЕМС. Для межового режиму [1] фактично вимагає нульової межової імовірності, що суперечить ППВ. У відповідності до правила трьох стандартів доцільно для такого режиму приймати значення Тоді однобічні показники ЕМС будуть визначатися з інтегральною 0,999, а діапазонні – з двома інтегральними ймовірностями: 0,001 і 0,999.

Висновки. 1. Від способу реалізації ППВ залежать техніко-економічні показники електроенергетичних систем.

2. Для задач електроенергетики рекомендується використовувати граничний спосіб реалізації ППВ.

Перелік посилань

1. ГОСТ 13109-97. Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Ук-раине с 01.01.2000.

© 2008 ДонНТУ