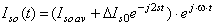 (3)
(3)COMPUTER SIMULATION OF THE TRANSIENTS IN AC MACHINES AT SHORT-CIRCUITS AND CONNECTIONS TO A NETWORK ON THE BASIS OF THE EXRERIMENTAL FREQUNCY-RESPONSE CHARACTERISTICS
Arcadiy Larin, Abdessalem Lamary
Donetsk State Technical University Donetsk (Ukraine)
Abstract — The mathematical models of the AC electrical machines developed on the basis of the experimental frequency-response characteristics are proposed in the paper. The latter ones are recommended for investigating the transient processes occurring at short-circuits and connections of the electrical machines to the bus bars of electrical system taking account of their rotor speed changes.
1. INTRODUCTION
It is a matter of familiar experience that the methods of frequency-response characteristics [1,5,6] have received wide acceptance in the scientific-research and engineering practical activity for investigating and evaluating the transient conditions of the AC machines in electrical systems. The above mentioned methods make possible to carry out the direct application of the experimental initial data in the form of frequency-response characteristics of the separate electrical system elements or of the system as a whole. Such an approach, in the special cases that the system internal structure is indeterminate, has much potential for yielding the more precise calculations of the transient processes.
The calculation technique for determining the transients by the use of the frequency-response characteristics of synchronous machine stator admittance in the direct, Yd(js), and quadrature, Yq(js), axes or the circle diagram of an induction motor was proposed in [1]. The graphic-analytical methods for determining the armature current and electromagnetic torque of the synchronous machine were developed in the cited monagraph too. The methods being considered allow to carry out more accurate calculations of the transient processes taking into account the following characteristic features:
• electromagnetic asymmetry of the rotor;
• representation of the turbogenerator solid rotor by means of the equivalent circuits corresponding to the high order transfer function of the damper system;
• current displacement in the windings of electrical machines;
• saturation phenomenon in the main and leakage paths of the magnetic fluxes of the AC machines;
• external impedance inserted in the armature winding of the AC machine.
The above mentioned methods did not get wide dissemination in due course though.
The great amount of information on the frequency-response characteristics of the synchronous machines and induction motors compiled by now and availability of the developed method designed for synthesising the equivalent circuits adequately reflecting the initial frequency-response characteristics of the AC electrical machines open up fresh opportunities for improving and further development of the frequency-response methods for investigating the transients in electrical machines.
The objective of the paper is to develop the mathematical models of the AC machines based on the experimental frequency-response characteristics for investigating the transients at short-circuits and connections of the AC machines in electrical system taking into consideration the occurring speed changes of the AC machine rotor.
2. BASIC RELATIONS
The mathematical relations realising the graphic-analytical approach [1] to determining the components of the stator phase current and electromagnetic torque at short-circuits or connections of the synchronous machines rotating at the synchronous speed to the electrical system are obtained in [2]. When the machine with the rotor asymmetry operates at the short-circuit with the speed changes relative to the synchronous speed or it is connected to the network at the given slip, determining the components of the generalised stator current vector is carried out in the following way:
• we find the average value of the steady-state current Is0 av for the slip s at the first instant of the transient process
Is0 av = Yav(js)s0 (1)
where
Yav(js) = (Yd(js) + Yq(js))/2
• we determine the pulsating component of the steady-state current
ΔIs0 = (Re[ΔY(js)s0] - Im[ΔY(js)s0])e-j2δ 0 (2)
where
Yav(js) = (Yd(js) - Yq(js))/2,
δ0 — angle between the q-axis of the rotor and the voltage vector at the infinite bus of an electrical system;
• we find the changes in the steady-state current with time, taking into account the difference in the rotor parameters on axes of its electrical and magnetic symmetry,
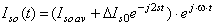 (3)
(3)• we determine the aperiodic current component
Is1 av = Yav(js)-(1-s) (4)
and the periodic current of the frequency close to the doubled one
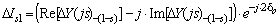 (5)
(5)Aperiodic current and the current component caused by the rotor asymmetry are changed in accordance with the following expression
 (6)
(6)The natural angular frequency of the aperiodic current vector, ωn, and the time constant of its decaying, τa, are defined for the average complex admittance Yav(js) at the slip s = -(1-s) by equations
 , (7)
, (7)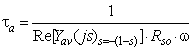 . (8)
. (8)The initial value of the periodic component of the transient current, Is2, is determined by recognising that
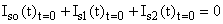 .
. Generally, the initial value of the current vector Is2(t)t=0 does not coincide with the d-axis of a rotor (including the connections of the synchronous machine occurring at the angle δ0) resulting in aperiodic current components in both axes of the rotor symmetry.
Implementation of the method proposed is associated with representing the initial frequency-response characteristics in the form of equivalent circuits in the d- and q-axis of a synchronous machine. The latter ones, e.g., the equivalent circuit in d-axis shown in Figure 1 may be used for determining the changes in the periodic current components with time [3].

The mentioned equivalent circuits allow to obtain the initial values (Is2 dk, Is2 ql) and the time constants (τdk, τql) of the exponential components of the periodic armature current Is2(t). So in the d- and q-axis we have

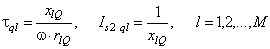 , (9)
, (9)From the above, it might be assumed that the time-dependence of the periodic current follows the law

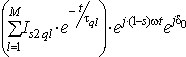 (10)
(10) where N, M = quantity of the elementary equivalent circuits of the rotor in d- and q-axis, respectively.
In the general case the initial Is2 current components in the d- and q-axis should be converted in proportion to the projection of the Is2 current vector on the direct, Is2d, and quadrature Is2q rotor axes, e.g.,

 (11)
(11)where φ = argument of the Is2(t)t=0 current vector (the angle between the current vector and the real axis of the complex plain).
Тhen

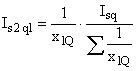 (12)
(12)The total generalised vector of the transient armature current comprises the vector sum of separate components:
 (13)
(13)where V = voltage across the terminals of an armature winding at the short-circuit condition or connection of a synchronous machine to the network.
The instantaneous values of the phase currents are determined as a projections of the generalised current vector on the motionless time axes of the appropriate phases:


 (14)
(14) where α(t) = time-dependent argument of the total generalised vector of the armature current.
It is evident that the dynamic properties of an induction machine can be described in full measure by means of a single frequency-response characteristic, Y(js). In this case, the expressions obtained above will not contain the additional current components ΔIs0 and ΔIs1. There are no needs in decomposition of the Is2 current on the d- and q-axis components either.
In accordance with the general approach the electromagnetic torque is determined using the current and flux linkage complexes, regardless of the rotor symmetry of the AC machine, by the expression:
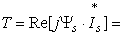
 (15)
(15)The magnetic linkages in (15) can be presented more detail as follows:
 (16)
(16)As may be seen from the equations (15) and (16), the electromagnetic torque can be presented as the sum of the vector products of the currents by flux linkage components. For example, the product of the vector Is0 by the vector Ψs0 produces the steady-state torque being numerically equal to the vertical projection of the current vector at the rated voltage across the terminals of the stator winding. The influence of the separate current and torque components on the features of the transient process having been analysed, it is possible to simplify the mathematical model of an electrical machine with the given accuracy.
At researching the electromechanical transients connected with the speed variations of AC machine rotor one should consider the simultaneous solution of the equations deduced above and the supplementary equation of the rotor relative motion. The latter one can be written in the following form:
 (17)
(17)where Tmech = shaft torque developed by the prime mover; M = inertia constant.
3. PROBLEM ALGORITHM
If the influence of the rotor acceleration is not taken into account the following problem algorithm considering the rotor speed changes can be suggested:
• the transient process is divided into small uniform intervals of time;
• the speed increment over the given interval is determined by solving the equation (17) as follows:
• the sustained component of the Is0 current is calculated at the constant speed obtained for the given time interval;
• the amplitude of the Is1 current component decaying with the time constant τa is calculated at the initial value of the rotor speed (at the beginning of the first interval);
• the natural angular frequency, ωn, and the time constant , τa, of the aperiodic currant component are re-counted using equation (7), (8) in relation to the slip changes of a rotor;
• the amplitude of the Is2 current component caused by the transient currents in the rotor circuits is determined at the rotor slip corresponding to the first instant of the process.
It should be pointed out that the angular speed of the Is2 current being taken into account in (10) varies with the slip changes. The rotor slip dependence of the natural angular frequency and the time constant of decaying the magnetic flux Ψs1 are taken into account by equation (16).
4. ESTIMATION OF THE MODEL VALIDITY
The efficiency of application of the frequency-response characteristics for calculating the transient processes can be demonstrated with the following examples:
1. Short-circuit at the terminals of the stator winding and connection to the network without excitation of the model turbogenerator of the МТ-30 type (Snom = 30 kVA, Vnom = 414 V, Inom = 41.8 A, xd = 1,453; xq = 1,394; Rs0 = 0,00624)
In the case being considered the influence of the sign and initial slip value at connecting the generator to the network as well as the influence of the rotor speed changes at the transient conditions were analysed.
2. Connection to the network of the unexcited turbogenerator of the ТГВ-200 type (Snom = 235 MVA, Vnom = 15.75 kV, Inom = 8635 A, xd = 1,9; xq = 1,89; Rs0 = 0,0012)
When calculating the electromechanical transients the errors being brought about by simplifying the complicated equivalent circuits, reflecting the electromagnetic asymmetry of the solid rotor, were considered.
3. Starting of the induction motor of the ДАЗО-1914-10/12А type (Рnom = 1500 кW; Inom = 204 А; Vnom = 6000 V) from the no-load condition, and three-phase short-circuit at its terminals.
Estimation of the results obtained, when using the techniques proposed above, was carried out by comparison with the appropriate calculations made by the use of algorithms based on numerical integrating the system of the differential Parc-Gorev equations. The frequency-response characteristics reflecting the dynamic properties of the AC machines being studied were obtained experimentally from the DC decay in the armature winding at standstill test [5].
Computer programs realising the above mentioned algorithms for calculating the electromechanical transients in AC machines were elaborated within the framework of the MathCAD 7.0.
The time-dependence of changing the generalised stator current vector and the electromagnetic running torque at connection the unexcited model generator to the network under the various initial rotor slips were carried out without the account and in view of changing the rotor speed at transients. The invariable rotor speed was simulated by way of setting the great value of the inertia constant.
As follows from comparison of the results obtained for the given slip values, equal to 0; 0,01; 0,03; 0,05 and 0,1p.u., the changes in the time-dependence of the generalised stator current vector and electromagnetic torque practically does not differ from the analogous calculations made on the basis of the Parc-Gorev equations. In these cases the difference in the maximum values of the similar operating variables being compared did not exceed 10,4%. The typical changes in the transients differ not at all. So, when making use of the static frequency-response characteristics, one can infer that the electromagnetic processes may be identified with a sufficiently high degree of accuracy.
The analysis of the transients calculated with taking into consideration the rotor speed changes, following the connection of the model generator, points to some differences in the time-dependent variables. By way of example, in the Figure 2 are shown the results of calculating the transients at connection the unexcited model machine to the network with the field winding short-circuited.
The calculations carried out in compliance with the system of Parc-Gorev equations (see dotted line) reflect the features connected with changes in the current, , and electromagnetic torque , , with the rotor speed changes. The time dependence of the slip in the case under consideration has the oscillatory character. Mathematical simulation based on the static characteristics (see solid line) brings about the monotonous changes in the rotor slip under the transient process. Meanwhile, the resultant time of approaching the rotor speed to the synchronous one, being estimated at the instant a rotor slip for the second time passes through zero, practically agrees with the time being determined from the solid line obtained at simulating the transients by means of the method proposed. As may be seen from the Figure 2, as a whole, the distinguishing features of the variables being considered are in close agreement; their maximum values appearing at the initial stage of the transient process correlate well with the data got without regard for speed changes of the rotor.
In the Figure 3 are given the curves reflecting the changes in the variables at the short-circuit on the terminals of the induction motor ДАЗО-1914-10/12А type.

The quantities of the motor equivalent circuits synthesised in accordance with [4] having three parallel branches and the magnetising one, separated in the manner as is shown in the Figure 1, are as follows (in per unit on machine base):
Xσ + Xμ = 2,19; X1 = 0,271; X2 = 1,179; X13 = 0,717; R1 = 0,0055; R2 = 0,1139; R3 = 0,624.
The comparative analysis of the results obtained by calculating the generalised stator current vector, Is, and electromagnetic torque, T, calculated by various methods points to their close agreement because of the maximum values of the mentioned variables differ less than 7,8%.
The analysis of the electromechanical transients at starting the non-loaded motor also indicates to the satisfactory coinciding of the results obtained by using the mentioned calculation techniques. In particular, the starting time determined by the technique proposed differs from the same parameter obtained through the use of the Parc Gorev equations less than 9,2%.
As is seen from the Figure 4, the electromagnetic transients within the time interval from 0 up to 0.1 s correspond closely with the results obtained by the Parc-Gorev equation (see dotted line).
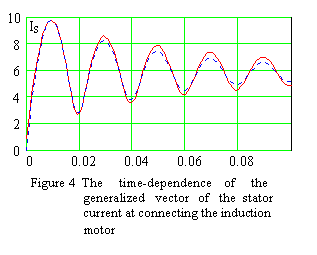
The mentioned acceptable results are attributable to the fact that the change in the motor speed takes place at the small rotor acceleration. In this case, the application of the frequency-response characteristics of a machine does not introduce large errors into calculation of the transient processes. When the rotor speed is close to the rated value there are considerable deviations in the changes of the current and electromagnetic torque with time.
As may be inferred from the research, the mentioned deviations decrease with increasing the inertia constant, M, and the loading factor of the induction motor. The transients in this case are accompanied by the less acceleration of a rotor.
The investigation of the transients called forth by connection of the unexcited turbogenerator ТГВ-200 type to the network was carried out with the use of the equivalent circuits containing five parallel branches in d- and q-axis [3]. It was ascertained that the errors being introduced in the transient processes by reducing the quantity of the circuit branches, describing the physical properties of the solid rotor, to three do not exceed the errors in a frequency domain equal to 11%.
5. CONCLUSION
The proposed mathematical models of the AC machines based on the experimental frequency-response characteristics allow to investigate the transients processes at short-circuits and connection of the machines to the network without solution of the conventional differential equations.
6. REFERENCES
1. Казовский Е.Я. Переходные процессы вэлектрических машинах переменного тока. — М.: Изд-во АН СССР, 1962. — 624 с.
2. Ларин А.М., Ларина И.И., Гуедиди Фаузи.Упрощенная модель синхронной машины для расчета трехфазных коротких замыканий с учетом многоконтурности и несимметрии ротора. Научные труды ДонГТУ, серия Электротехника и энергетика, вып.4. Донецк, 1999. — С. 60-64.
3. Ларин А.М., Ламари Абдессалем. Определение параметров схем замещения турбогенераторов, отображающих электромагнитную несимметрию их массивных роторов. Научные труды ДонГТУ, серия: Электротехника и энергетика, вып.4. Донецк, 1999. — С. 65-68.
4. Рогозин Г.Г., Ларин А.М. Расчет параметров эквивалентных роторных контуров синхронных машин по их экспериментальным частотным характеристикам / Электричество, 1974, № 6. С.10 - 13.
5. Рогозин Г.Г. Определение электромагнитных параметров машин переменного тока. — К.: Техніка, 1992. — 168 с.
6. Применение частотных методов в электроэнергетическом исследовании. Труды СибНИИЭ / Под ред. Лукашова Э.С. — Новосибирск, 1972, вып. 21. — 294 с.