|
|
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТРЁХФАЗНОГО АСИНХРОННОГО ДВИГАТЕЛЯ С ФАЗНЫМ РОТОРОМ
Омельченко Е.Я.
"ЭЛЕКТРОТЕХНИКА №6/04" с. 19-24
Регулируемый электропривод (ЭП) переменного тока становится самым распространённым, существенно потеснившим позиции ЭП постоянного тока. Современные транзисторные преобразователи частоты, тиристорные устройства плавного пуска на базе микропроцессорных устройств надёжно и качественно управляют асинхронными и синхронными двигателями. Реостатное регулирование, асинхронно-вентильные каскады, индукционные регуляторы широко используются для управления асинхронными двигателями с фазным ротором. Развитие альтернативного направления в теории управления на основе вычислительных технологий искусственных нейронных сетей и генетических алгоритмов глобальной оптимизации позволят существенно улучшить существующие алгоритмы и развить новые направления.
Поэтому разработка математической модели асинхронного двигателя, позволяющей максимально возможно учесть механизм электромагнитомеханического пространственного преобразования и управления энергией трёхфазного переменного тока в механическую энергию с возможностью формирования электромеханических обратных связей является актуальной научно-технической задачей, для решения которой современные вычислительные средства не вносят каких-либо ограничений.
Постановка задачи исследования
Существующие математические модели разработаны в основном в двухфазном варианте для сосредоточенных обмоток статора и ротора, учитывается только основная гармоника напряжения, тока, потокосцепления, практически не учитывается насыщение магнитной цепи и наведённые вихревые токи [1,2]. В трёхфазном исполнении насыщение рассматривалось для сосредоточенных обмоток без учёта вихревых токов [3].
Исходные положения для разработки математической модели асинхронного электродвигателя с фазным ротором:
1. Обмотки статора и ротора распределены по пазам и состоят из нескольких катушечных групп. В пространственной волне МДС необходимо учитывать эти особенности обмоток.
2. Учёт насыщения магнитной системы проводится по цепи "зубец статора-зазор-зубец ротора".
3. Не учитываются зубцовые пульсации потока при вращении ротора.
4. Контуры вихревых токов представлены короткозамкнутыми витками в каждом зубце.
5. Индуктивности потоков рассеяния статорных и роторных обмоток считаются постоянными и не зависящими от насыщения основной магнитной цепи.
6. Расчёт основных переменных ведётся в абсолютных величинах.
7. Имеется возможность изменять активное сопротивление роторной обмотки в функции частоты вращения ротора.
8. В качестве входного воздействия, приложенного к фазам статора и ротора, используются напряжения любом амплитуды, формы, частоты, фазы.
9. Выходные координаты для контроля и внешнего управления:
токи статора и ротора;
электромагнитный момент ротора;
угловая скорость вращения и угол поворота ротора.
10. Внутренние координаты для контроля: МДС, индукции и вихревые токи в зубцах
статора и ротора:
- потокосцепления и ЭДС статорных и роторных обмоток;
потери в меди статора и ротора, потери на вихревые токи.
11. Возмущающие воздействия.
- реактивный момент сопротивления от трения в подшипниках;
- момент сопротивления от рабочего механизма.
Далее в статье приведены исходные уравнения для модели и структурная схема модели.
Результаты моделирования
В соответствии с математической моделью в среде программных и инструментальных средств Matlab 6,5 разработана структурная схема математической модели трёхфазного асинхронного двигателя с фазным ротором ADF96.mdl, позволяющая рассчитывать переходные процессы выделенных переменных электрической машины с учётом распределён¬ных обмоток, насыщения стали и вихревых то¬ков в зубцах статора и ротора. В программе статорная обмотка выполнена с q = 3 (n1 = 9), а роторная с q = 2 (п2 = 6).
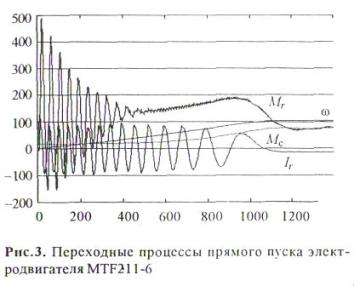 На рис. 3 в абсолютных величинах [6] приведены кривые переходных процессов угловой скорости вращения, электромагнитного момента ротора, тока роторной обмотки при прямом пуске электродвигателя MTF211-6. Переходный процесс момента Mr при прямом пуске имеет характерный участок колебаний от начала пуска до t = 0,25 с частотой 50 Гц, связанный со свободной составляющей переходного процесса. Бросок момента доходит до 480 Нм, критический момент равен 190 Нм (2,46 Мн). Максимальный ток ротора равен 130 А. В установившемся режиме ток статора, момент и угловая скорость практически совпадают с номинальными данными двигателя, что говорит об адекватности разработанной модели и реального двигателя.
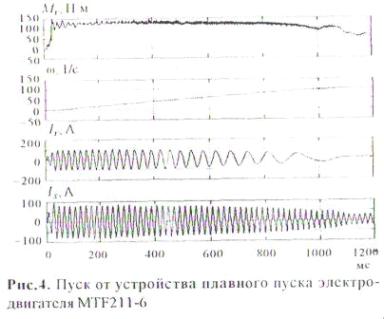 Результаты моделирования процесса пуска АД от устройства плавного пуска (УПП) представлены на рис.4 (электромагнитный момент, угловая скорость вращения, токи ротора и статора фазы А). Пуск АД от УПП [7] в соответствии с разработанными алгоритмами (спадание сигнала управления от 0,75 до 0,52 за время от 0 до 1 с и дальнейшее нарастание до 1 при 1,2 с) характеризуется плавным нарастанием момента за 35 мс до 120 Нм и временем пуска 1,07 с. Прерывистый ток начинается с 0,5 с и заканчивается после 1,1 с. Пуск линейный. Наличие прерывистого тока статора приводит к незначительным высокочастотным колебаниям момента.
Выводы
1. Разработанная математическая модель трёхфазного асинхронного двигателя проводит расчёт переходных процессов с учётом распределённых обмоток, насыщения и вихревых токов в зубцах статора и ротора.
2. Разработанная модель реализована с помощью программных средств пакета Matlab 6,5.
3. С помощью программы можно проводить исследования систем электропривода при питании двигателя от различных преобразователей и устройств плавного пуска, каскадных схем регулирования, синхронизированных асинхронных двигателей.
4. Программа позволяет проводить пересчёт координат двигателя для реализации замкнутых систем регулирования.
Список литературы
1. Kлючев В.И. Теория электропривода: Учебник для вузов. М.:Энергоатомиздат, 1985.
2. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. Екатеринбург: УРО РАН, 2000.
3. Омельченко Е. Я., Харламов А.В. Моделировапие на ЭВМ переходных процессов в асинхронном электроприводе // Электротехнические системы и комплексы: межвуз сб. науч. тр Магнитогорск: МГТУ, 1998. Вып.4 С. 36-42.
4. Омельченко Е.Я. Характеристики двигателей в электроприводе: Учебное пособие. Магнитогорск: MГТУ 2004.
5. Корн Г., Корн Т.- Справочник но математике (для научных работников и инженеров). М.: Наука, 1974.
6. Омельченко Е.Я. Математическая модель асинхронного электродвигателя с фазным ротором // Электротехнические системы и комплексы: межвуз. сб. научн. тр. Магнитогорск: МГТУ, 2006. Вып. 12 С.100-108.
7. Омельченко Е.Я. Разработка алгоритмов управления устройств плавного пуска // Оптимизация режимов работы электротехнических систем: межвуз. сб. науч. тр. Красноярск: ИПЦ КГТУ, 2006. С.90-96.
|
|