Кинетика H2S и CO2 в водных растворах МЭА, ДЭА и МДЭА
Чтобы определить скорость поглощения CO2 и H2S водным раствором амина, скорости реакций этих
газов в растворах должны быть определены. Эта статья представляет обширный литературный обзор по кинетике реакций
CO2 и H2S в водных растворах чистого MЭA, ДЭA, и MДЭA и смесей MЭA/MДЭA и ДЭA/MДЭA.
Важные реакции и механизмы, по которым эти реакции протекают в жидкой фазе, разъяснены.
Концентрации гидроокиси,
сульфида, и ионов карбоната, которые получены по этим реакциям, являются относительно маленькими.
Можно с уверенностью предположить, что концентрации этих ионов в жидкой фазе равны их соответствующим массовым
концентрациям. Концентрацию воды в жидкой фазе можно также счесть незадействованной кинетикой реакций в жидкой фазе.
Концентрации остальных соединений нужно учитывать, чтобы точно вычислить степень поглощения CO2 и H2S.
1. Механизм реакции H2S в водных растворах алканоламинов
H2S реагирует с MЭA, ДЭA, или MДЭA, с образованием гидросульфида и присоединением протона амина согласно с
ледующим реакциям:
MEA:
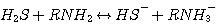
(3.1)
DEA:
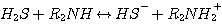
(3.2)
MDEA:
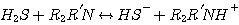
(3.3)
Механизм каждой из этих реакций сопровождается передачей протона. Поэтому, все эти реакции считают мгновенными с
бесконечной скоростью реакции. Концентрации в жидкой фазе реагентов и продуктов этих реакций при равновесии:
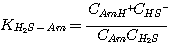
(3.4)
где Am относится к MЭA, ДЭA или MДЭA. Константы равновесия KH2S-Am, связаны с константами
равновесия:
MEA:
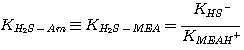
(3.5)
DEA:
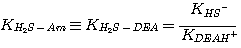
(3.6)
MDEA:
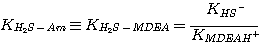
(3.7)
Скорость поглощения H2S водным раствором, содержащим первичный амин может быть определена аналитически.
Это было сделано Одном и др. 1970. Они использовали теорию двух фаз, чтобы получить общее аналитическое выражение
фактора повышения для систем, описывающихся единственной мгновенной химической реакцией. Для систем, содержащих смеси
аминов, амины конкурируют, чтобы поглотить H2S. Дифференциальные уравнения для этих систем слишком усложнены,
чтобы быть решенными аналитически. Константа равновесия реакции образования сульфида (уравнение 2.5) слишком мала, чтобы
воздействовать на концентрацию бисульфида в жидкой фазе. Поэтому пренебрежение этой реакции в жидкой фазе практически не
влияет на вычисление скорости абсорбции H2S.
2. Механизм реакции CO2 в водных растворах алканоламинов
В любом водном растворе CO2 реагирует с водой и гидроокисью согласно следующим реакциям:
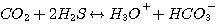
(3.8)
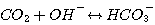
(3.9)
Взаимодействиие CO2 по реакции 3.8 имеет первый порядок относительно CO2.
Константа скорости этой реакции была представлена как функция температуры Пирсентом и сотрудниками (Пирсент и др., 1956):
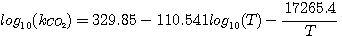
(3.10)
Скорость диссоциации CO2 по реакции 3.9 в соответствии с элементарной кинетикой может быть определена:
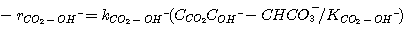
(3.11)
Астарита и др. (1983) изучил эффект ионной силы на константе скорости,
kCO2-OH-. Они преобразовали выражение, первоначально представленное Шервудом и др.
(1975), чтобы включить ионную силу:
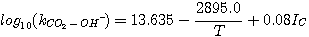
(3.12)
где IC - ионная сила, зависящая от концентрации:
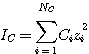
(3.13)
Реакции (3.8) и (3.9) очень медленны по сравнению с реакциями CO2 с MЭA или ДЭA, особенно для CO2
меньше чем 0.5. Пренебрежение этими реакциями, не повлияет на вычисление скорости абсорбции CO2.
Следовательно, жидкофазная концентрация иона бикарбоната постоянна в системах, содержащих только MЭA или ДЭA.
С другой стороны, MДЭA, как полагают, катализирует эти реакции. В результате пренебрежения изменением концентрации
бикарбоната в системах, содержащих MДЭA могло бы привести к ошибке в вычислении скорости поглощения CO2.
2.1 Реакция CO2 с MЭA and ДЭA
Поглощение CO2CO2 водными растворами MЭA и ДЭA было экстенсивно изучено в литературе. Использовалось
несколько методов, чтобы собрать кинетические данные. Они включают ламинарный поток движения фаз, интенсивное смешивание,
движение фаз, диффузию через пористые тела и мешалки. Описания методологии и экспериментального набора предоставили Ван
Кревелен и Хофтижер (1948), Нанг и Гилл (1963), Колдери и Харрис (1976), Алварез и др. (1980), Гласскок (1990), Хогендурн
и др. (1993), и Ko и Ли (2000).
Реакция MЭA с CO2 была изучена несколькими исследователями, включая Астарита 1961, Ледера 1971, Сада и др.
1976, Хикита и др. 1977, Ладдага и Данквертса, 1981 и Блаувгоффа и др. 1984. Есть общее мнение среди исследователей, что
реакция CO2 с MЭA имеет кинетику второго порядка. Второй порядок константы скорости этой реакции был
представлен как функция температуры Хикитом и др. 1977. Пересмотр данных, сделанных Блаувгоффом и др. 1984 и Бартем и др.
1986 подтвердил результаты Хикита и др. 1977.
Блэнк и Демариас (1984) пересмотрели данные и предложенные механизмы скорости реакции CO2 с ДЭA.
Они выяснили, что результаты исследователей значительно отличаются. Зависимость скорости реакции от концентрации ДЭA
была сообщена как первый или второй порядок. Константы скорости, о которых сообщают, были также не сопоставимы.
Блаувгофф и др. (1984) пересмотрели сообщения о кинетических данных для этой системы. Они сделали вывод, что скорость
реакции CO2 с ДЭA слишком усложнена, чтобы быть интерпретированной простой кинетической моделью. Они в
дальнейшем показали, что амфотерный механизм применим в большинстве публикационных данных о кинетике CO2-ДЭA.
Амфотерный механизм был принят Гласскоком (1990), чтобы представить кинетические данные CO2 в первичном и
вторичном алканоламинах. Этот механизм был первоначально предложен Капловом в 1968 и представлен в химической инженерной
литературе Данквертсом в 1979. Согласно этому механизму, CO2 реагирует с МЭА или ДЭА с образованием нестойкого
соединения Z. Соединение мгновенно нейтрализуется каким-нибудь основанием Bi присутствующим в растворе с образованием
карбоната амина и протонированного основания,
BiH+:
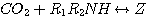
(3.14)

(3.15)
где Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
и R2 ≡ H и R1 для MЭA and ДЭA, respectively.
Реакция 3.14 – это скорость взаимодействия CO2; следовательно скорость исчезновения CO2:
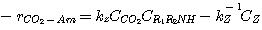
(3.16)
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
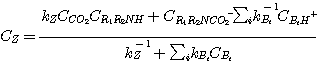
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
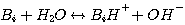
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
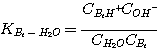
(3.21)
или:
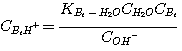
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
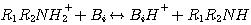
(3.25)
где:
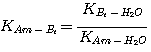
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
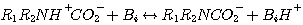
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
1. Механизм реакции H2S в водных растворах алканоламинов
H2S реагирует с MЭA, ДЭA, или MДЭA, с образованием гидросульфида и присоединением протона амина согласно с
ледующим реакциям:
MEA:
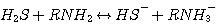
(3.1)
DEA:
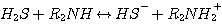
(3.2)
MDEA:
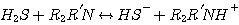
(3.3)
Механизм каждой из этих реакций сопровождается передачей протона. Поэтому, все эти реакции считают мгновенными с
бесконечной скоростью реакции. Концентрации в жидкой фазе реагентов и продуктов этих реакций при равновесии:
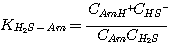
(3.4)
где Am относится к MЭA, ДЭA или MДЭA. Константы равновесия KH2S-Am, связаны с константами
равновесия:
MEA:
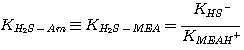
(3.5)
DEA:
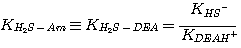
(3.6)
MDEA:
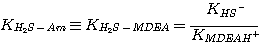
(3.7)
Скорость поглощения H2S водным раствором, содержащим первичный амин может быть определена аналитически.
Это было сделано Одном и др. 1970. Они использовали теорию двух фаз, чтобы получить общее аналитическое выражение
фактора повышения для систем, описывающихся единственной мгновенной химической реакцией. Для систем, содержащих смеси
аминов, амины конкурируют, чтобы поглотить H2S. Дифференциальные уравнения для этих систем слишком усложнены,
чтобы быть решенными аналитически. Константа равновесия реакции образования сульфида (уравнение 2.5) слишком мала, чтобы
воздействовать на концентрацию бисульфида в жидкой фазе. Поэтому пренебрежение этой реакции в жидкой фазе практически не
влияет на вычисление скорости абсорбции H2S.
2. Механизм реакции CO2 в водных растворах алканоламинов
В любом водном растворе CO2 реагирует с водой и гидроокисью согласно следующим реакциям:
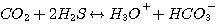
(3.8)
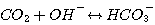
(3.9)
Взаимодействиие CO2 по реакции 3.8 имеет первый порядок относительно CO2.
Константа скорости этой реакции была представлена как функция температуры Пирсентом и сотрудниками (Пирсент и др., 1956):
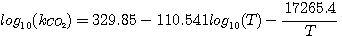
(3.10)
Скорость диссоциации CO2 по реакции 3.9 в соответствии с элементарной кинетикой может быть определена:
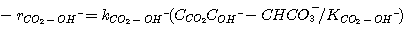
(3.11)
Астарита и др. (1983) изучил эффект ионной силы на константе скорости,
kCO2-OH-. Они преобразовали выражение, первоначально представленное Шервудом и др.
(1975), чтобы включить ионную силу:
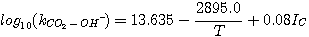
(3.12)
где IC - ионная сила, зависящая от концентрации:
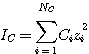
(3.13)
Реакции (3.8) и (3.9) очень медленны по сравнению с реакциями CO2 с MЭA или ДЭA, особенно для CO2
меньше чем 0.5. Пренебрежение этими реакциями, не повлияет на вычисление скорости абсорбции CO2.
Следовательно, жидкофазная концентрация иона бикарбоната постоянна в системах, содержащих только MЭA или ДЭA.
С другой стороны, MДЭA, как полагают, катализирует эти реакции. В результате пренебрежения изменением концентрации
бикарбоната в системах, содержащих MДЭA могло бы привести к ошибке в вычислении скорости поглощения CO2.
2.1 Реакция CO2 с MЭA and ДЭA
Поглощение CO2CO2 водными растворами MЭA и ДЭA было экстенсивно изучено в литературе. Использовалось
несколько методов, чтобы собрать кинетические данные. Они включают ламинарный поток движения фаз, интенсивное смешивание,
движение фаз, диффузию через пористые тела и мешалки. Описания методологии и экспериментального набора предоставили Ван
Кревелен и Хофтижер (1948), Нанг и Гилл (1963), Колдери и Харрис (1976), Алварез и др. (1980), Гласскок (1990), Хогендурн
и др. (1993), и Ko и Ли (2000).
Реакция MЭA с CO2 была изучена несколькими исследователями, включая Астарита 1961, Ледера 1971, Сада и др.
1976, Хикита и др. 1977, Ладдага и Данквертса, 1981 и Блаувгоффа и др. 1984. Есть общее мнение среди исследователей, что
реакция CO2 с MЭA имеет кинетику второго порядка. Второй порядок константы скорости этой реакции был
представлен как функция температуры Хикитом и др. 1977. Пересмотр данных, сделанных Блаувгоффом и др. 1984 и Бартем и др.
1986 подтвердил результаты Хикита и др. 1977.
Блэнк и Демариас (1984) пересмотрели данные и предложенные механизмы скорости реакции CO2 с ДЭA.
Они выяснили, что результаты исследователей значительно отличаются. Зависимость скорости реакции от концентрации ДЭA
была сообщена как первый или второй порядок. Константы скорости, о которых сообщают, были также не сопоставимы.
Блаувгофф и др. (1984) пересмотрели сообщения о кинетических данных для этой системы. Они сделали вывод, что скорость
реакции CO2 с ДЭA слишком усложнена, чтобы быть интерпретированной простой кинетической моделью. Они в
дальнейшем показали, что амфотерный механизм применим в большинстве публикационных данных о кинетике CO2-ДЭA.
Амфотерный механизм был принят Гласскоком (1990), чтобы представить кинетические данные CO2 в первичном и
вторичном алканоламинах. Этот механизм был первоначально предложен Капловом в 1968 и представлен в химической инженерной
литературе Данквертсом в 1979. Согласно этому механизму, CO2 реагирует с МЭА или ДЭА с образованием нестойкого
соединения Z. Соединение мгновенно нейтрализуется каким-нибудь основанием Bi присутствующим в растворе с образованием
карбоната амина и протонированного основания,
BiH+:
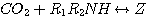
(3.14)

(3.15)
где Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
и R2 ≡ H и R1 для MЭA and ДЭA, respectively.
Реакция 3.14 – это скорость взаимодействия CO2; следовательно скорость исчезновения CO2:
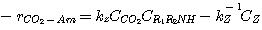
(3.16)
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
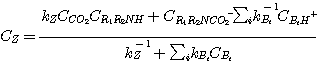
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
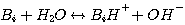
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
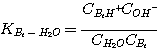
(3.21)
или:
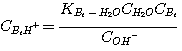
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
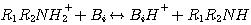
(3.25)
где:
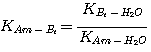
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
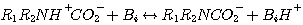
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
| MEA: |
|
(3.1) |
| DEA: |
|
(3.2) |
| MDEA: |
|
(3.3) |
Механизм каждой из этих реакций сопровождается передачей протона. Поэтому, все эти реакции считают мгновенными с
бесконечной скоростью реакции. Концентрации в жидкой фазе реагентов и продуктов этих реакций при равновесии:
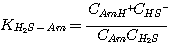
(3.4)
где Am относится к MЭA, ДЭA или MДЭA. Константы равновесия KH2S-Am, связаны с константами
равновесия:
MEA:
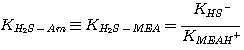
(3.5)
DEA:
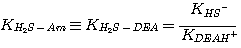
(3.6)
MDEA:
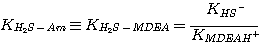
(3.7)
Скорость поглощения H2S водным раствором, содержащим первичный амин может быть определена аналитически.
Это было сделано Одном и др. 1970. Они использовали теорию двух фаз, чтобы получить общее аналитическое выражение
фактора повышения для систем, описывающихся единственной мгновенной химической реакцией. Для систем, содержащих смеси
аминов, амины конкурируют, чтобы поглотить H2S. Дифференциальные уравнения для этих систем слишком усложнены,
чтобы быть решенными аналитически. Константа равновесия реакции образования сульфида (уравнение 2.5) слишком мала, чтобы
воздействовать на концентрацию бисульфида в жидкой фазе. Поэтому пренебрежение этой реакции в жидкой фазе практически не
влияет на вычисление скорости абсорбции H2S.
2. Механизм реакции CO2 в водных растворах алканоламинов
В любом водном растворе CO2 реагирует с водой и гидроокисью согласно следующим реакциям:
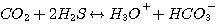
(3.8)
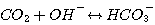
(3.9)
Взаимодействиие CO2 по реакции 3.8 имеет первый порядок относительно CO2.
Константа скорости этой реакции была представлена как функция температуры Пирсентом и сотрудниками (Пирсент и др., 1956):
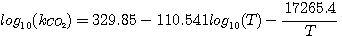
(3.10)
Скорость диссоциации CO2 по реакции 3.9 в соответствии с элементарной кинетикой может быть определена:
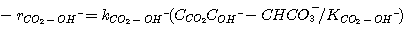
(3.11)
Астарита и др. (1983) изучил эффект ионной силы на константе скорости,
kCO2-OH-. Они преобразовали выражение, первоначально представленное Шервудом и др.
(1975), чтобы включить ионную силу:
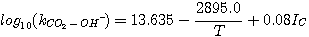
(3.12)
где IC - ионная сила, зависящая от концентрации:
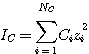
(3.13)
Реакции (3.8) и (3.9) очень медленны по сравнению с реакциями CO2 с MЭA или ДЭA, особенно для CO2
меньше чем 0.5. Пренебрежение этими реакциями, не повлияет на вычисление скорости абсорбции CO2.
Следовательно, жидкофазная концентрация иона бикарбоната постоянна в системах, содержащих только MЭA или ДЭA.
С другой стороны, MДЭA, как полагают, катализирует эти реакции. В результате пренебрежения изменением концентрации
бикарбоната в системах, содержащих MДЭA могло бы привести к ошибке в вычислении скорости поглощения CO2.
2.1 Реакция CO2 с MЭA and ДЭA
Поглощение CO2CO2 водными растворами MЭA и ДЭA было экстенсивно изучено в литературе. Использовалось
несколько методов, чтобы собрать кинетические данные. Они включают ламинарный поток движения фаз, интенсивное смешивание,
движение фаз, диффузию через пористые тела и мешалки. Описания методологии и экспериментального набора предоставили Ван
Кревелен и Хофтижер (1948), Нанг и Гилл (1963), Колдери и Харрис (1976), Алварез и др. (1980), Гласскок (1990), Хогендурн
и др. (1993), и Ko и Ли (2000).
Реакция MЭA с CO2 была изучена несколькими исследователями, включая Астарита 1961, Ледера 1971, Сада и др.
1976, Хикита и др. 1977, Ладдага и Данквертса, 1981 и Блаувгоффа и др. 1984. Есть общее мнение среди исследователей, что
реакция CO2 с MЭA имеет кинетику второго порядка. Второй порядок константы скорости этой реакции был
представлен как функция температуры Хикитом и др. 1977. Пересмотр данных, сделанных Блаувгоффом и др. 1984 и Бартем и др.
1986 подтвердил результаты Хикита и др. 1977.
Блэнк и Демариас (1984) пересмотрели данные и предложенные механизмы скорости реакции CO2 с ДЭA.
Они выяснили, что результаты исследователей значительно отличаются. Зависимость скорости реакции от концентрации ДЭA
была сообщена как первый или второй порядок. Константы скорости, о которых сообщают, были также не сопоставимы.
Блаувгофф и др. (1984) пересмотрели сообщения о кинетических данных для этой системы. Они сделали вывод, что скорость
реакции CO2 с ДЭA слишком усложнена, чтобы быть интерпретированной простой кинетической моделью. Они в
дальнейшем показали, что амфотерный механизм применим в большинстве публикационных данных о кинетике CO2-ДЭA.
Амфотерный механизм был принят Гласскоком (1990), чтобы представить кинетические данные CO2 в первичном и
вторичном алканоламинах. Этот механизм был первоначально предложен Капловом в 1968 и представлен в химической инженерной
литературе Данквертсом в 1979. Согласно этому механизму, CO2 реагирует с МЭА или ДЭА с образованием нестойкого
соединения Z. Соединение мгновенно нейтрализуется каким-нибудь основанием Bi присутствующим в растворе с образованием
карбоната амина и протонированного основания,
BiH+:
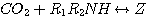
(3.14)

(3.15)
где Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
и R2 ≡ H и R1 для MЭA and ДЭA, respectively.
Реакция 3.14 – это скорость взаимодействия CO2; следовательно скорость исчезновения CO2:
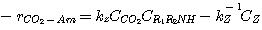
(3.16)
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
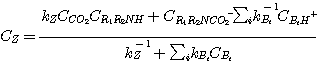
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
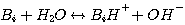
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
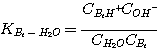
(3.21)
или:
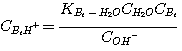
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
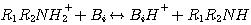
(3.25)
где:
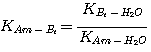
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
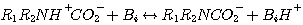
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.4) |
где Am относится к MЭA, ДЭA или MДЭA. Константы равновесия KH2S-Am, связаны с константами равновесия:
| MEA: |
|
(3.5) |
| DEA: |
|
(3.6) |
| MDEA: |
|
(3.7) |
Скорость поглощения H2S водным раствором, содержащим первичный амин может быть определена аналитически.
Это было сделано Одном и др. 1970. Они использовали теорию двух фаз, чтобы получить общее аналитическое выражение
фактора повышения для систем, описывающихся единственной мгновенной химической реакцией. Для систем, содержащих смеси
аминов, амины конкурируют, чтобы поглотить H2S. Дифференциальные уравнения для этих систем слишком усложнены,
чтобы быть решенными аналитически. Константа равновесия реакции образования сульфида (уравнение 2.5) слишком мала, чтобы
воздействовать на концентрацию бисульфида в жидкой фазе. Поэтому пренебрежение этой реакции в жидкой фазе практически не
влияет на вычисление скорости абсорбции H2S.
2. Механизм реакции CO2 в водных растворах алканоламинов
В любом водном растворе CO2 реагирует с водой и гидроокисью согласно следующим реакциям:
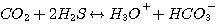
(3.8)
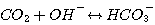
(3.9)
Взаимодействиие CO2 по реакции 3.8 имеет первый порядок относительно CO2.
Константа скорости этой реакции была представлена как функция температуры Пирсентом и сотрудниками (Пирсент и др., 1956):
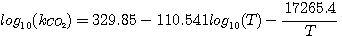
(3.10)
Скорость диссоциации CO2 по реакции 3.9 в соответствии с элементарной кинетикой может быть определена:
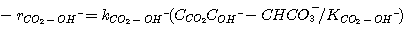
(3.11)
Астарита и др. (1983) изучил эффект ионной силы на константе скорости,
kCO2-OH-. Они преобразовали выражение, первоначально представленное Шервудом и др.
(1975), чтобы включить ионную силу:
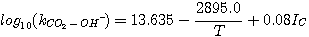
(3.12)
где IC - ионная сила, зависящая от концентрации:
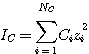
(3.13)
Реакции (3.8) и (3.9) очень медленны по сравнению с реакциями CO2 с MЭA или ДЭA, особенно для CO2
меньше чем 0.5. Пренебрежение этими реакциями, не повлияет на вычисление скорости абсорбции CO2.
Следовательно, жидкофазная концентрация иона бикарбоната постоянна в системах, содержащих только MЭA или ДЭA.
С другой стороны, MДЭA, как полагают, катализирует эти реакции. В результате пренебрежения изменением концентрации
бикарбоната в системах, содержащих MДЭA могло бы привести к ошибке в вычислении скорости поглощения CO2.
2.1 Реакция CO2 с MЭA and ДЭA
Поглощение CO2CO2 водными растворами MЭA и ДЭA было экстенсивно изучено в литературе. Использовалось
несколько методов, чтобы собрать кинетические данные. Они включают ламинарный поток движения фаз, интенсивное смешивание,
движение фаз, диффузию через пористые тела и мешалки. Описания методологии и экспериментального набора предоставили Ван
Кревелен и Хофтижер (1948), Нанг и Гилл (1963), Колдери и Харрис (1976), Алварез и др. (1980), Гласскок (1990), Хогендурн
и др. (1993), и Ko и Ли (2000).
Реакция MЭA с CO2 была изучена несколькими исследователями, включая Астарита 1961, Ледера 1971, Сада и др.
1976, Хикита и др. 1977, Ладдага и Данквертса, 1981 и Блаувгоффа и др. 1984. Есть общее мнение среди исследователей, что
реакция CO2 с MЭA имеет кинетику второго порядка. Второй порядок константы скорости этой реакции был
представлен как функция температуры Хикитом и др. 1977. Пересмотр данных, сделанных Блаувгоффом и др. 1984 и Бартем и др.
1986 подтвердил результаты Хикита и др. 1977.
Блэнк и Демариас (1984) пересмотрели данные и предложенные механизмы скорости реакции CO2 с ДЭA.
Они выяснили, что результаты исследователей значительно отличаются. Зависимость скорости реакции от концентрации ДЭA
была сообщена как первый или второй порядок. Константы скорости, о которых сообщают, были также не сопоставимы.
Блаувгофф и др. (1984) пересмотрели сообщения о кинетических данных для этой системы. Они сделали вывод, что скорость
реакции CO2 с ДЭA слишком усложнена, чтобы быть интерпретированной простой кинетической моделью. Они в
дальнейшем показали, что амфотерный механизм применим в большинстве публикационных данных о кинетике CO2-ДЭA.
Амфотерный механизм был принят Гласскоком (1990), чтобы представить кинетические данные CO2 в первичном и
вторичном алканоламинах. Этот механизм был первоначально предложен Капловом в 1968 и представлен в химической инженерной
литературе Данквертсом в 1979. Согласно этому механизму, CO2 реагирует с МЭА или ДЭА с образованием нестойкого
соединения Z. Соединение мгновенно нейтрализуется каким-нибудь основанием Bi присутствующим в растворе с образованием
карбоната амина и протонированного основания,
BiH+:
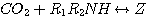
(3.14)

(3.15)
где Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
и R2 ≡ H и R1 для MЭA and ДЭA, respectively.
Реакция 3.14 – это скорость взаимодействия CO2; следовательно скорость исчезновения CO2:
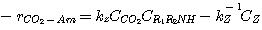
(3.16)
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
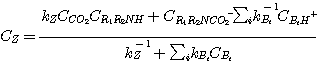
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
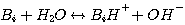
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
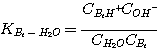
(3.21)
или:
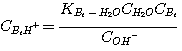
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
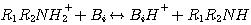
(3.25)
где:
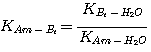
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
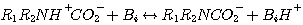
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
2. Механизм реакции CO2 в водных растворах алканоламинов
В любом водном растворе CO2 реагирует с водой и гидроокисью согласно следующим реакциям:
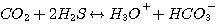
(3.8)
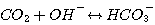
(3.9)
Взаимодействиие CO2 по реакции 3.8 имеет первый порядок относительно CO2.
Константа скорости этой реакции была представлена как функция температуры Пирсентом и сотрудниками (Пирсент и др., 1956):
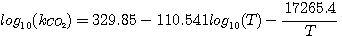
(3.10)
Скорость диссоциации CO2 по реакции 3.9 в соответствии с элементарной кинетикой может быть определена:
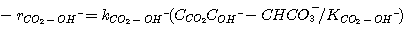
(3.11)
Астарита и др. (1983) изучил эффект ионной силы на константе скорости,
kCO2-OH-. Они преобразовали выражение, первоначально представленное Шервудом и др.
(1975), чтобы включить ионную силу:
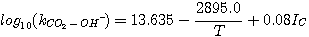
(3.12)
где IC - ионная сила, зависящая от концентрации:
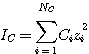
(3.13)
Реакции (3.8) и (3.9) очень медленны по сравнению с реакциями CO2 с MЭA или ДЭA, особенно для CO2
меньше чем 0.5. Пренебрежение этими реакциями, не повлияет на вычисление скорости абсорбции CO2.
Следовательно, жидкофазная концентрация иона бикарбоната постоянна в системах, содержащих только MЭA или ДЭA.
С другой стороны, MДЭA, как полагают, катализирует эти реакции. В результате пренебрежения изменением концентрации
бикарбоната в системах, содержащих MДЭA могло бы привести к ошибке в вычислении скорости поглощения CO2.
2.1 Реакция CO2 с MЭA and ДЭA
Поглощение CO2CO2 водными растворами MЭA и ДЭA было экстенсивно изучено в литературе. Использовалось
несколько методов, чтобы собрать кинетические данные. Они включают ламинарный поток движения фаз, интенсивное смешивание,
движение фаз, диффузию через пористые тела и мешалки. Описания методологии и экспериментального набора предоставили Ван
Кревелен и Хофтижер (1948), Нанг и Гилл (1963), Колдери и Харрис (1976), Алварез и др. (1980), Гласскок (1990), Хогендурн
и др. (1993), и Ko и Ли (2000).
Реакция MЭA с CO2 была изучена несколькими исследователями, включая Астарита 1961, Ледера 1971, Сада и др.
1976, Хикита и др. 1977, Ладдага и Данквертса, 1981 и Блаувгоффа и др. 1984. Есть общее мнение среди исследователей, что
реакция CO2 с MЭA имеет кинетику второго порядка. Второй порядок константы скорости этой реакции был
представлен как функция температуры Хикитом и др. 1977. Пересмотр данных, сделанных Блаувгоффом и др. 1984 и Бартем и др.
1986 подтвердил результаты Хикита и др. 1977.
Блэнк и Демариас (1984) пересмотрели данные и предложенные механизмы скорости реакции CO2 с ДЭA.
Они выяснили, что результаты исследователей значительно отличаются. Зависимость скорости реакции от концентрации ДЭA
была сообщена как первый или второй порядок. Константы скорости, о которых сообщают, были также не сопоставимы.
Блаувгофф и др. (1984) пересмотрели сообщения о кинетических данных для этой системы. Они сделали вывод, что скорость
реакции CO2 с ДЭA слишком усложнена, чтобы быть интерпретированной простой кинетической моделью. Они в
дальнейшем показали, что амфотерный механизм применим в большинстве публикационных данных о кинетике CO2-ДЭA.
Амфотерный механизм был принят Гласскоком (1990), чтобы представить кинетические данные CO2 в первичном и
вторичном алканоламинах. Этот механизм был первоначально предложен Капловом в 1968 и представлен в химической инженерной
литературе Данквертсом в 1979. Согласно этому механизму, CO2 реагирует с МЭА или ДЭА с образованием нестойкого
соединения Z. Соединение мгновенно нейтрализуется каким-нибудь основанием Bi присутствующим в растворе с образованием
карбоната амина и протонированного основания,
BiH+:
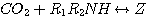
(3.14)

(3.15)
где Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
и R2 ≡ H и R1 для MЭA and ДЭA, respectively.
Реакция 3.14 – это скорость взаимодействия CO2; следовательно скорость исчезновения CO2:
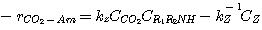
(3.16)
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
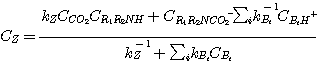
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
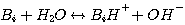
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
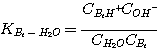
(3.21)
или:
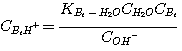
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
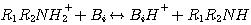
(3.25)
где:
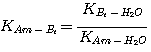
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
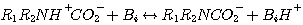
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.8) |
|
|
(3.9) |
Взаимодействиие CO2 по реакции 3.8 имеет первый порядок относительно CO2.
Константа скорости этой реакции была представлена как функция температуры Пирсентом и сотрудниками (Пирсент и др., 1956):
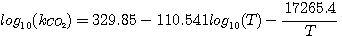
(3.10)
Скорость диссоциации CO2 по реакции 3.9 в соответствии с элементарной кинетикой может быть определена:
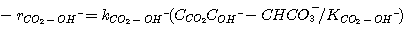
(3.11)
Астарита и др. (1983) изучил эффект ионной силы на константе скорости,
kCO2-OH-. Они преобразовали выражение, первоначально представленное Шервудом и др.
(1975), чтобы включить ионную силу:
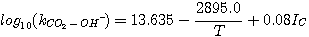
(3.12)
где IC - ионная сила, зависящая от концентрации:
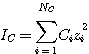
(3.13)
Реакции (3.8) и (3.9) очень медленны по сравнению с реакциями CO2 с MЭA или ДЭA, особенно для CO2
меньше чем 0.5. Пренебрежение этими реакциями, не повлияет на вычисление скорости абсорбции CO2.
Следовательно, жидкофазная концентрация иона бикарбоната постоянна в системах, содержащих только MЭA или ДЭA.
С другой стороны, MДЭA, как полагают, катализирует эти реакции. В результате пренебрежения изменением концентрации
бикарбоната в системах, содержащих MДЭA могло бы привести к ошибке в вычислении скорости поглощения CO2.
2.1 Реакция CO2 с MЭA and ДЭA
Поглощение CO2CO2 водными растворами MЭA и ДЭA было экстенсивно изучено в литературе. Использовалось
несколько методов, чтобы собрать кинетические данные. Они включают ламинарный поток движения фаз, интенсивное смешивание,
движение фаз, диффузию через пористые тела и мешалки. Описания методологии и экспериментального набора предоставили Ван
Кревелен и Хофтижер (1948), Нанг и Гилл (1963), Колдери и Харрис (1976), Алварез и др. (1980), Гласскок (1990), Хогендурн
и др. (1993), и Ko и Ли (2000).
Реакция MЭA с CO2 была изучена несколькими исследователями, включая Астарита 1961, Ледера 1971, Сада и др.
1976, Хикита и др. 1977, Ладдага и Данквертса, 1981 и Блаувгоффа и др. 1984. Есть общее мнение среди исследователей, что
реакция CO2 с MЭA имеет кинетику второго порядка. Второй порядок константы скорости этой реакции был
представлен как функция температуры Хикитом и др. 1977. Пересмотр данных, сделанных Блаувгоффом и др. 1984 и Бартем и др.
1986 подтвердил результаты Хикита и др. 1977.
Блэнк и Демариас (1984) пересмотрели данные и предложенные механизмы скорости реакции CO2 с ДЭA.
Они выяснили, что результаты исследователей значительно отличаются. Зависимость скорости реакции от концентрации ДЭA
была сообщена как первый или второй порядок. Константы скорости, о которых сообщают, были также не сопоставимы.
Блаувгофф и др. (1984) пересмотрели сообщения о кинетических данных для этой системы. Они сделали вывод, что скорость
реакции CO2 с ДЭA слишком усложнена, чтобы быть интерпретированной простой кинетической моделью. Они в
дальнейшем показали, что амфотерный механизм применим в большинстве публикационных данных о кинетике CO2-ДЭA.
Амфотерный механизм был принят Гласскоком (1990), чтобы представить кинетические данные CO2 в первичном и
вторичном алканоламинах. Этот механизм был первоначально предложен Капловом в 1968 и представлен в химической инженерной
литературе Данквертсом в 1979. Согласно этому механизму, CO2 реагирует с МЭА или ДЭА с образованием нестойкого
соединения Z. Соединение мгновенно нейтрализуется каким-нибудь основанием Bi присутствующим в растворе с образованием
карбоната амина и протонированного основания,
BiH+:
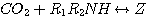
(3.14)

(3.15)
где Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
и R2 ≡ H и R1 для MЭA and ДЭA, respectively.
Реакция 3.14 – это скорость взаимодействия CO2; следовательно скорость исчезновения CO2:
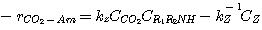
(3.16)
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
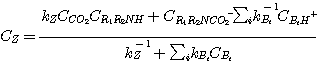
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
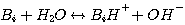
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
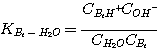
(3.21)
или:
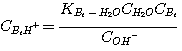
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
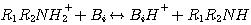
(3.25)
где:
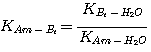
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
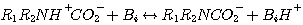
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.10) |
Скорость диссоциации CO2 по реакции 3.9 в соответствии с элементарной кинетикой может быть определена:
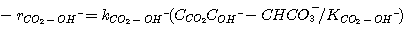
(3.11)
Астарита и др. (1983) изучил эффект ионной силы на константе скорости,
kCO2-OH-. Они преобразовали выражение, первоначально представленное Шервудом и др.
(1975), чтобы включить ионную силу:
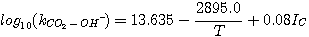
(3.12)
где IC - ионная сила, зависящая от концентрации:
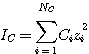
(3.13)
Реакции (3.8) и (3.9) очень медленны по сравнению с реакциями CO2 с MЭA или ДЭA, особенно для CO2
меньше чем 0.5. Пренебрежение этими реакциями, не повлияет на вычисление скорости абсорбции CO2.
Следовательно, жидкофазная концентрация иона бикарбоната постоянна в системах, содержащих только MЭA или ДЭA.
С другой стороны, MДЭA, как полагают, катализирует эти реакции. В результате пренебрежения изменением концентрации
бикарбоната в системах, содержащих MДЭA могло бы привести к ошибке в вычислении скорости поглощения CO2.
2.1 Реакция CO2 с MЭA and ДЭA
Поглощение CO2CO2 водными растворами MЭA и ДЭA было экстенсивно изучено в литературе. Использовалось
несколько методов, чтобы собрать кинетические данные. Они включают ламинарный поток движения фаз, интенсивное смешивание,
движение фаз, диффузию через пористые тела и мешалки. Описания методологии и экспериментального набора предоставили Ван
Кревелен и Хофтижер (1948), Нанг и Гилл (1963), Колдери и Харрис (1976), Алварез и др. (1980), Гласскок (1990), Хогендурн
и др. (1993), и Ko и Ли (2000).
Реакция MЭA с CO2 была изучена несколькими исследователями, включая Астарита 1961, Ледера 1971, Сада и др.
1976, Хикита и др. 1977, Ладдага и Данквертса, 1981 и Блаувгоффа и др. 1984. Есть общее мнение среди исследователей, что
реакция CO2 с MЭA имеет кинетику второго порядка. Второй порядок константы скорости этой реакции был
представлен как функция температуры Хикитом и др. 1977. Пересмотр данных, сделанных Блаувгоффом и др. 1984 и Бартем и др.
1986 подтвердил результаты Хикита и др. 1977.
Блэнк и Демариас (1984) пересмотрели данные и предложенные механизмы скорости реакции CO2 с ДЭA.
Они выяснили, что результаты исследователей значительно отличаются. Зависимость скорости реакции от концентрации ДЭA
была сообщена как первый или второй порядок. Константы скорости, о которых сообщают, были также не сопоставимы.
Блаувгофф и др. (1984) пересмотрели сообщения о кинетических данных для этой системы. Они сделали вывод, что скорость
реакции CO2 с ДЭA слишком усложнена, чтобы быть интерпретированной простой кинетической моделью. Они в
дальнейшем показали, что амфотерный механизм применим в большинстве публикационных данных о кинетике CO2-ДЭA.
Амфотерный механизм был принят Гласскоком (1990), чтобы представить кинетические данные CO2 в первичном и
вторичном алканоламинах. Этот механизм был первоначально предложен Капловом в 1968 и представлен в химической инженерной
литературе Данквертсом в 1979. Согласно этому механизму, CO2 реагирует с МЭА или ДЭА с образованием нестойкого
соединения Z. Соединение мгновенно нейтрализуется каким-нибудь основанием Bi присутствующим в растворе с образованием
карбоната амина и протонированного основания,
BiH+:
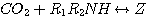
(3.14)

(3.15)
где Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
и R2 ≡ H и R1 для MЭA and ДЭA, respectively.
Реакция 3.14 – это скорость взаимодействия CO2; следовательно скорость исчезновения CO2:
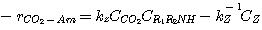
(3.16)
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
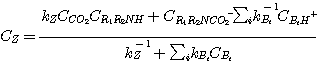
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
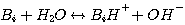
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
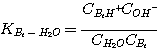
(3.21)
или:
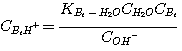
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
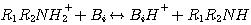
(3.25)
где:
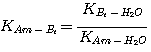
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
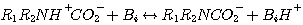
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.11) |
Астарита и др. (1983) изучил эффект ионной силы на константе скорости,
kCO2-OH-. Они преобразовали выражение, первоначально представленное Шервудом и др.
(1975), чтобы включить ионную силу:
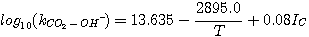
(3.12)
где IC - ионная сила, зависящая от концентрации:
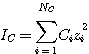
(3.13)
Реакции (3.8) и (3.9) очень медленны по сравнению с реакциями CO2 с MЭA или ДЭA, особенно для CO2
меньше чем 0.5. Пренебрежение этими реакциями, не повлияет на вычисление скорости абсорбции CO2.
Следовательно, жидкофазная концентрация иона бикарбоната постоянна в системах, содержащих только MЭA или ДЭA.
С другой стороны, MДЭA, как полагают, катализирует эти реакции. В результате пренебрежения изменением концентрации
бикарбоната в системах, содержащих MДЭA могло бы привести к ошибке в вычислении скорости поглощения CO2.
2.1 Реакция CO2 с MЭA and ДЭA
Поглощение CO2CO2 водными растворами MЭA и ДЭA было экстенсивно изучено в литературе. Использовалось
несколько методов, чтобы собрать кинетические данные. Они включают ламинарный поток движения фаз, интенсивное смешивание,
движение фаз, диффузию через пористые тела и мешалки. Описания методологии и экспериментального набора предоставили Ван
Кревелен и Хофтижер (1948), Нанг и Гилл (1963), Колдери и Харрис (1976), Алварез и др. (1980), Гласскок (1990), Хогендурн
и др. (1993), и Ko и Ли (2000).
Реакция MЭA с CO2 была изучена несколькими исследователями, включая Астарита 1961, Ледера 1971, Сада и др.
1976, Хикита и др. 1977, Ладдага и Данквертса, 1981 и Блаувгоффа и др. 1984. Есть общее мнение среди исследователей, что
реакция CO2 с MЭA имеет кинетику второго порядка. Второй порядок константы скорости этой реакции был
представлен как функция температуры Хикитом и др. 1977. Пересмотр данных, сделанных Блаувгоффом и др. 1984 и Бартем и др.
1986 подтвердил результаты Хикита и др. 1977.
Блэнк и Демариас (1984) пересмотрели данные и предложенные механизмы скорости реакции CO2 с ДЭA.
Они выяснили, что результаты исследователей значительно отличаются. Зависимость скорости реакции от концентрации ДЭA
была сообщена как первый или второй порядок. Константы скорости, о которых сообщают, были также не сопоставимы.
Блаувгофф и др. (1984) пересмотрели сообщения о кинетических данных для этой системы. Они сделали вывод, что скорость
реакции CO2 с ДЭA слишком усложнена, чтобы быть интерпретированной простой кинетической моделью. Они в
дальнейшем показали, что амфотерный механизм применим в большинстве публикационных данных о кинетике CO2-ДЭA.
Амфотерный механизм был принят Гласскоком (1990), чтобы представить кинетические данные CO2 в первичном и
вторичном алканоламинах. Этот механизм был первоначально предложен Капловом в 1968 и представлен в химической инженерной
литературе Данквертсом в 1979. Согласно этому механизму, CO2 реагирует с МЭА или ДЭА с образованием нестойкого
соединения Z. Соединение мгновенно нейтрализуется каким-нибудь основанием Bi присутствующим в растворе с образованием
карбоната амина и протонированного основания,
BiH+:
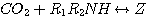
(3.14)

(3.15)
где Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
и R2 ≡ H и R1 для MЭA and ДЭA, respectively.
Реакция 3.14 – это скорость взаимодействия CO2; следовательно скорость исчезновения CO2:
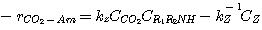
(3.16)
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
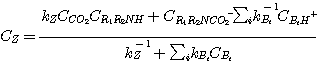
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
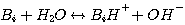
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
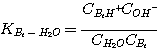
(3.21)
или:
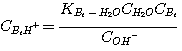
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
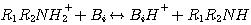
(3.25)
где:
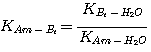
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
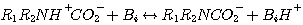
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.12) |
где IC - ионная сила, зависящая от концентрации:
|
|
(3.13) |
Реакции (3.8) и (3.9) очень медленны по сравнению с реакциями CO2 с MЭA или ДЭA, особенно для CO2
меньше чем 0.5. Пренебрежение этими реакциями, не повлияет на вычисление скорости абсорбции CO2.
Следовательно, жидкофазная концентрация иона бикарбоната постоянна в системах, содержащих только MЭA или ДЭA.
С другой стороны, MДЭA, как полагают, катализирует эти реакции. В результате пренебрежения изменением концентрации
бикарбоната в системах, содержащих MДЭA могло бы привести к ошибке в вычислении скорости поглощения CO2.
2.1 Реакция CO2 с MЭA and ДЭA
Поглощение CO2CO2 водными растворами MЭA и ДЭA было экстенсивно изучено в литературе. Использовалось
несколько методов, чтобы собрать кинетические данные. Они включают ламинарный поток движения фаз, интенсивное смешивание,
движение фаз, диффузию через пористые тела и мешалки. Описания методологии и экспериментального набора предоставили Ван
Кревелен и Хофтижер (1948), Нанг и Гилл (1963), Колдери и Харрис (1976), Алварез и др. (1980), Гласскок (1990), Хогендурн
и др. (1993), и Ko и Ли (2000).
Реакция MЭA с CO2 была изучена несколькими исследователями, включая Астарита 1961, Ледера 1971, Сада и др.
1976, Хикита и др. 1977, Ладдага и Данквертса, 1981 и Блаувгоффа и др. 1984. Есть общее мнение среди исследователей, что
реакция CO2 с MЭA имеет кинетику второго порядка. Второй порядок константы скорости этой реакции был
представлен как функция температуры Хикитом и др. 1977. Пересмотр данных, сделанных Блаувгоффом и др. 1984 и Бартем и др.
1986 подтвердил результаты Хикита и др. 1977.
Блэнк и Демариас (1984) пересмотрели данные и предложенные механизмы скорости реакции CO2 с ДЭA.
Они выяснили, что результаты исследователей значительно отличаются. Зависимость скорости реакции от концентрации ДЭA
была сообщена как первый или второй порядок. Константы скорости, о которых сообщают, были также не сопоставимы.
Блаувгофф и др. (1984) пересмотрели сообщения о кинетических данных для этой системы. Они сделали вывод, что скорость
реакции CO2 с ДЭA слишком усложнена, чтобы быть интерпретированной простой кинетической моделью. Они в
дальнейшем показали, что амфотерный механизм применим в большинстве публикационных данных о кинетике CO2-ДЭA.
Амфотерный механизм был принят Гласскоком (1990), чтобы представить кинетические данные CO2 в первичном и
вторичном алканоламинах. Этот механизм был первоначально предложен Капловом в 1968 и представлен в химической инженерной
литературе Данквертсом в 1979. Согласно этому механизму, CO2 реагирует с МЭА или ДЭА с образованием нестойкого
соединения Z. Соединение мгновенно нейтрализуется каким-нибудь основанием Bi присутствующим в растворе с образованием
карбоната амина и протонированного основания,
BiH+:
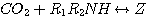
(3.14)

(3.15)
где Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
и R2 ≡ H и R1 для MЭA and ДЭA, respectively.
Реакция 3.14 – это скорость взаимодействия CO2; следовательно скорость исчезновения CO2:
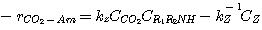
(3.16)
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
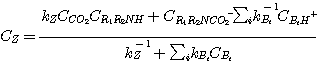
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
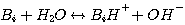
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
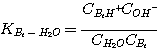
(3.21)
или:
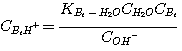
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
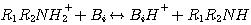
(3.25)
где:
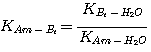
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
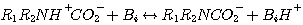
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
2.1 Реакция CO2 с MЭA and ДЭA
Поглощение CO2CO2 водными растворами MЭA и ДЭA было экстенсивно изучено в литературе. Использовалось
несколько методов, чтобы собрать кинетические данные. Они включают ламинарный поток движения фаз, интенсивное смешивание,
движение фаз, диффузию через пористые тела и мешалки. Описания методологии и экспериментального набора предоставили Ван
Кревелен и Хофтижер (1948), Нанг и Гилл (1963), Колдери и Харрис (1976), Алварез и др. (1980), Гласскок (1990), Хогендурн
и др. (1993), и Ko и Ли (2000).
Реакция MЭA с CO2 была изучена несколькими исследователями, включая Астарита 1961, Ледера 1971, Сада и др.
1976, Хикита и др. 1977, Ладдага и Данквертса, 1981 и Блаувгоффа и др. 1984. Есть общее мнение среди исследователей, что
реакция CO2 с MЭA имеет кинетику второго порядка. Второй порядок константы скорости этой реакции был
представлен как функция температуры Хикитом и др. 1977. Пересмотр данных, сделанных Блаувгоффом и др. 1984 и Бартем и др.
1986 подтвердил результаты Хикита и др. 1977.
Блэнк и Демариас (1984) пересмотрели данные и предложенные механизмы скорости реакции CO2 с ДЭA.
Они выяснили, что результаты исследователей значительно отличаются. Зависимость скорости реакции от концентрации ДЭA
была сообщена как первый или второй порядок. Константы скорости, о которых сообщают, были также не сопоставимы.
Блаувгофф и др. (1984) пересмотрели сообщения о кинетических данных для этой системы. Они сделали вывод, что скорость
реакции CO2 с ДЭA слишком усложнена, чтобы быть интерпретированной простой кинетической моделью. Они в
дальнейшем показали, что амфотерный механизм применим в большинстве публикационных данных о кинетике CO2-ДЭA.
Амфотерный механизм был принят Гласскоком (1990), чтобы представить кинетические данные CO2 в первичном и
вторичном алканоламинах. Этот механизм был первоначально предложен Капловом в 1968 и представлен в химической инженерной
литературе Данквертсом в 1979. Согласно этому механизму, CO2 реагирует с МЭА или ДЭА с образованием нестойкого
соединения Z. Соединение мгновенно нейтрализуется каким-нибудь основанием Bi присутствующим в растворе с образованием
карбоната амина и протонированного основания,
BiH+:
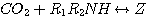
(3.14)

(3.15)
где Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
и R2 ≡ H и R1 для MЭA and ДЭA, respectively.
Реакция 3.14 – это скорость взаимодействия CO2; следовательно скорость исчезновения CO2:
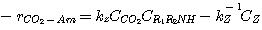
(3.16)
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
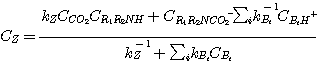
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
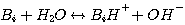
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
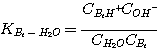
(3.21)
или:
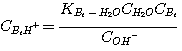
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
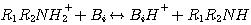
(3.25)
где:
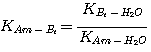
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
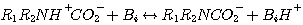
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.14) |
|
|
(3.15) |
где Z ≡ R1R2NH+, R1 ≡ CH3CH2OH,
и R2 ≡ H и R1 для MЭA and ДЭA, respectively.
Реакция 3.14 – это скорость взаимодействия CO2; следовательно скорость исчезновения CO2:
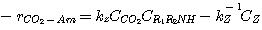
(3.16)
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
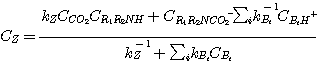
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
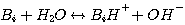
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
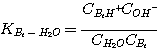
(3.21)
или:
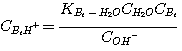
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
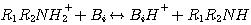
(3.25)
где:
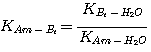
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
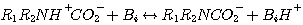
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.16) |
Т.к. амфотерный ион нестоек, его скорость образования равна нулю:

(3.17)
Рассчитать концентрацию амфотерного иона можно по формуле:
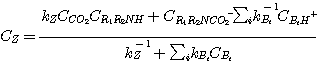
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
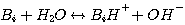
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
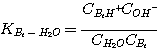
(3.21)
или:
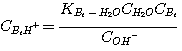
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
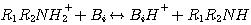
(3.25)
где:
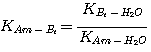
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
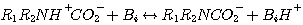
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.17) |
Рассчитать концентрацию амфотерного иона можно по формуле:
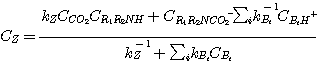
(3.18)
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
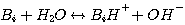
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
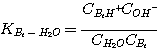
(3.21)
или:
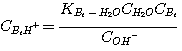
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
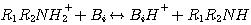
(3.25)
где:
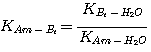
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
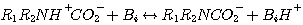
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.18) |
Введя замену уравнением 3.18 в уравнение 3.16 и, преобразуя его, получим:

(3.19)
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
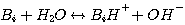
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
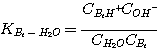
(3.21)
или:
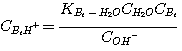
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
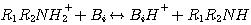
(3.25)
где:
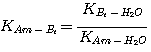
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
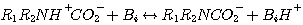
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.19) |
Уравнение 3.19 может быть упрощено отношением групп констант скорости к их соответствующим концентрациям равновесия
следующим образом. Рассмотрите реакцию воды с основанием:
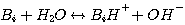
(3.20)
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
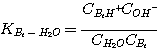
(3.21)
или:
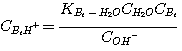
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
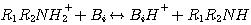
(3.25)
где:
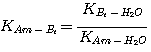
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
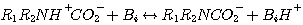
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.20) |
Эта реакция включает передачу протона, поэтому, реагенты и продукты этой реакции в момент равновесия:
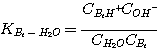
(3.21)
или:
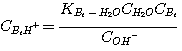
(3.22)
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
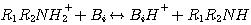
(3.25)
где:
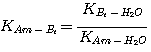
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
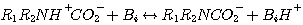
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.21) |
или:
|
|
(3.22) |
Амин может вести себя как основание и реагировать с водой согласно:

(3.23)
где:

(3.24)
Объединение реакций 3.20 и 3.23 дает:
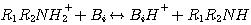
(3.25)
где:
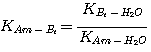
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
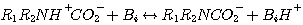
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.23) |
где:
|
|
(3.24) |
Объединение реакций 3.20 и 3.23 дает:
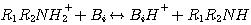
(3.25)
где:
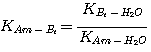
(3.26)
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
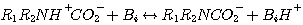
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.25) |
где:
|
|
(3.26) |
Реакция амина с амфотерным ионом дает:

(3.27)
Объединение реакций 3.25 и 3.27 дает:
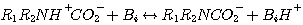
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.27) |
Объединение реакций 3.25 и 3.27 дает:
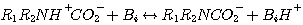
(3.28)
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.28) |
Сравнение реакций 3.15 и 3.28 дает:

(3.29)
или:

(3.30)
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.29) |
или:
|
|
(3.30) |
Добавление реакций 3.14 и 3.15 и замены амином дает:

(3.31)
где:

(3.32)
или:

(3.33)
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.31) |
где:
|
|
(3.32) |
или:
|
|
(3.33) |
Подставляя уравнения 3.24 и 3.33 в уравнение 3.30, имеем:

(3.34)
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.34) |
Подставляя уравнения 3.34 и 3.22 в уравнение 3.19 и преобразуя его, имеем:

(3.35)
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.35) |
Второй член в числителе уравнения (3.35) представляет собой концентрацию CO2, который находится в
равновесии с амином, карбаматом амина и присоединил протон амина, по реакции 3.31. Следовательно, это уравнение может
быть переписано как:

(3.36)
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.36) |
Как упомянуто, данные кинетики для системы CO2-MЭA имеют второй порядок. Уравнение 3.35 сокращается до
второго порядка, если вторым членом в знаменателе пренебречь, по сравнению с первым членом, получим:

(3.37)
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.37) |
Второй порядок константы скорости, полученный Хикитом и др. 1977 будет использоваться в этом исследовании, чтобы
вычислить скорость поглощения CO2 для систем, содержащих MЭA. Эта константа скорости представлена как функция
температуры:
MEA:

(3.38)
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
| MEA: |
|
(3.38) |
Напротив, первый член в знаменателе уравнения (3.35) незначителен по сравнению со вторым членом для
системы CO2-ДЭA:
DEA:

(3.39)
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
| DEA: |
|
(3.39) |
Уравнение 3.39 использовалось Ладдгом и Данквертсом 1981, Блаувгоффом и др. (1984), Верстигом и Ван Сваайж (1988), и
Гласскоком (1990), чтобы описать данные кинетики для системы CO2-ДЭА. Гласскок (1990) предположил, что амин и
вода – единственные основания, которые способствуют нейтрализации аморфного иона. Выражение скорости CO2-ДЭА,
сообщенное Гласскоком 1990, будет использоваться в этом исследовании. Это выражение представляют как:
DEA:

(3.40)
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
| DEA: |
|
(3.40) |
Константы скорости k'R1R2NH и k'H2O
представленные Гласскоком (1990), были извлечены от соответствующих данных кинетики и представлены как функции температуры

(3.41)

(3.42)
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.41) |
|
|
(3.42) |
2.2 Реакция CO2 с MДEA
CO2 реагирует косвенно с MДЭA в присутствии воды с образованием бикарбоната и присоединением протона
MДЭA. Три различных механизма были предложены для этой реакции (Барт и др. 1981). Первый механизм предполагает, что MДЭA
нейтрализует соединения, сформированные CO2-водными реакциями (реакции 3.8 и 3.9). Второй механизм
предполагает, что MДЭA связывается с водой перед реакцией с CO2:

(3.43)
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.43) |
Третий механизм описывается аморфным механизмом, описанным ранее для MЭA и ДЭA:

(3.44)
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.44) |
Амфотерный ион, сформированный мгновенно, реагирует с водой и гидроокисью, с образованием соответственно бикарбоната и
присоединением протона MДЭA и бикарбоната и MДЭA согласно:

(3.45)

(3.46)
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.45) |
|
|
(3.46) |
Принимая третий механизм и после процедуры, развитой ранее для MЭA и DЭA, следующее выражение получено для скорости
реакции CO2 с MДЭA:

(3.47)
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.47) |
Объединение реакций 3.44 с 3.45 и 3.44 с 3.46 дает:

(3.48)

(3.49)
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.48) |
|
|
(3.49) |
Реакция 3.48 может также быть получена от комбинаций следующих реакций:

(3.50)

(3.51)
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.50) |
|
|
(3.51) |
Отныне

(3.52)
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.52) |
Так как реакция 3.50 мгновенна, ее продукты и реагенты при равновесии:

(3.53)
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.53) |
Поэтому:

(3.54)
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.54) |
Реакция 3.49 может быть получена, комбинируя мгновенную реакцию разложения воды (уравнение 2.1) с реакцией 3.51, чтобы
получить:

(3.55)
или:

(3.56)
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.55) |
или:
|
|
(3.56) |
Замена уравнениями 3.54 и 3.56 в уравнение 3.47 и преобразование дает:

(3.57)
или:

(3.58)
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.57) |
или:
|
|
(3.58) |
Подобный происхождению MДA и ДЭA, второй член в числителе уравнения 3.58 представляет концентрацию CO2,
который находится в равновесии с бикарбонатом и ионами гидроокиси:

(3.59)
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.59) |
Уравнение 3.58 - общее выражение скорости для реакции CO2 с MДЭA или любым третичным амином.
В зависимости от величины второго члена знаменателя этого уравнения, можно получить две ограничивающих формы:

Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
Выражение скорости в этом случае уменьшается до:

(3.60)
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.60) |
Эта форма - по существу выражение, которое было бы получено, используя второй механизм. Много исследователей, включая
Хаймора и др. (1987), Хритчефильда (1988), Томкежа и др. (1989), Литтла и др. (1990), Рангавала и др. (1992), и Ко и Ли
(2000) принимали эту формулу, чтобы соответствовать данным скорости системы CO2-МДЭА. Константа скорости
реакции представлена как функция температуры:

(3.61)
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.61) |
Сравнивая среди публикуемых значений константы скорости при 195,15 К, получили вариацию от 2,5 до 8,8 л/моль/сек.

В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
В данном случае выражение скорости представляют как:

(3.62)
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.62) |
Гласскок (1990) показал, что эта формула принимает публикуемые данные лучше. Он использовал активность вместо
концентраций для получения констант скорости. В текущем исследовании выражение скорости, представленное первой формулой с
константой скорости, сообщенное Критчфилдом (1998), будет использоваться при моделировании кинетики
реакций CO2 с МДЭА. Константа скорости, представленная Критчфилдом, представлена как:

(3.63)
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
|
|
(3.63) |
2.3 Реакция CO2 со смесями MЭA-MДЭA and ДЭA-MДЭA
Поглощение CO2 водным раствором смесей MЭA-MДЭA и ДЭA-MДЭA была изучена Гласскоком и др. (1990),
Верстегом и др. (1990), Ранвалом и др. (1992), и Хагевиесем и др. (1995). Крайчфилд показал, что взаимодействие между
MДЭA и MЭA является незначительным. Поэтому выражения скорости (уравнение 3.37) для MЭA и (уравнение 3.60) для MДЭA все
еще применимы для смеси MЭA-MДЭA. Однако, для систем, содержащих ДЭA и MДЭA, последние ведут себя как основания, которое
нейтрализует амфотерный ион, образованный по реакции CO2 с ДЭA. Следовательно, выражение скорости
CO2-ДЭA для систем, содержащих ДЭA и MДЭA должно быть исправлено, добавляя влияние MДЭA на нейтрализацию
амфотерного иона:
DEA/MDEA:

(3.64)

Значение 468 м6/кмоль2/сек сообщено в тезисе Гласскок (1990) как константа скорости.
В этой работе, это значение используется для любой температуры, чтобы вычислить скорость абсорбции
CO2 в системах, содержащих смеси ДЭA и MДЭA. Следуя предложению Гласскока (1990), влиянием МДЭА на скорость
реакции CO2 с МЭА можно пренебрегать.
© ДонНТУ Комиссарова О.В. 2008
| DEA/MDEA: |
|
(3.64) |

|
||