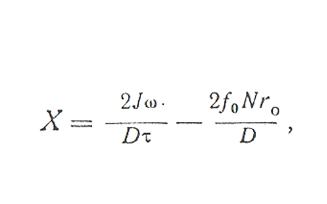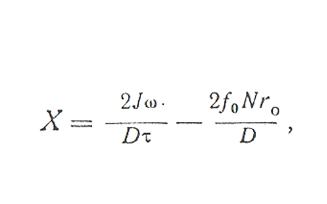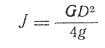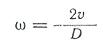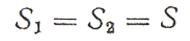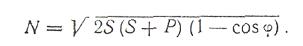Флоринский Ф.В. Динамика шахтного подъемного каната. Под ред. Савина Г.Н. М.: Углетехиздат, 1958 г. 239 с.
ТЕОРИЯ РАСЧЕТА СТАЛЬНЫХ ПОДЪЕМНЫХ КАНАТОВ
Сравнивая между собой наибольшие величины динамических напряжений, возникающих в упруго-вязком и упругом канатах постоянной длины, приходим к выводу, что затухание колебаний оказывает лишь небольшое влияние па уменьшение первого максимума динамических напряжений. Так как эти напряжения обычно составляют не более 40—50% наибольших полных напряжений, то уменьшение максимума последних, вызванное вязкими свойствами каната, будет еще менее ощутимым. При принятых нами величинах параметра вязкости, установленных на основании результатов испытания реального каната, уменьшение первого максимума полных напряжений в упруго-вязком канате по гравнению с.упругим не превысит 3—4%, а во многих случаях окажется ниже. К таким же результатам пришел Г. Н. Савин для канатов переменной длины.
Эти результаты приводят нас к выводу о необходимости расчета проволочного подъемного каната не как упруго-вязкой, а как упругой нити, что сделало нецелесообразным дальнейшее уточнение величины параметра вязкости .
Это положение также нашло свое отражение в работе Г. Н. Савина при рассмотрении канатов переменной длины.
В последующем изложении мы будем рассматривать подъемный канат исключительно как упругую нить постоянной длины.
О допускаемом напряжении для подъемного каната
Для расчета шахтных подъемных канатов широким распространением пользуется так называемый статический метод расчета. Этот метод заключается в том, что канат рассчитывается на простое растяжение как однородный стержень, подверженный действию только собственного веса и веса концевого груза Чтобы учесть влияние остальных сил, принимают повышенный запас прочности. Предполагается, что этот запас покрывает все усилия, развивающиеся в канате, как статические, так и динамические.
Дополнительная растягивающая сила
Определим приближенно дополнительную растягивающую силу,
являющуюся результатом влияния инерции шкива. Обозначим: эту силу через X. На основании теоремы о моменте количества движения, считая силу X не зависящей от времени і, и предположив, что шкив остановился за промежуток времени (сек.), имеем
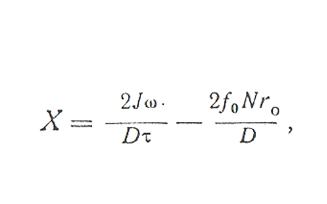
где
J-момент инерции шкива;
D-его диаметр;
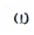-угловая скорость шкива до резкой остановки барабана;
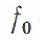-коэффициент трения между втулкой шкива и осью;
N-давление на ось;
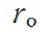-радиус оси.
Заменим:
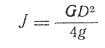
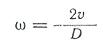
где
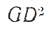-маховый момент шкива, значения которого для некоторых шкивов даны в таблице 1
g-ускорение тяжести.
Выражение получит вид
Давление на ось шкива
где
Р-вес шкива.
Последнее выражение можно упростить, считая приблеженно
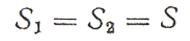
тогда
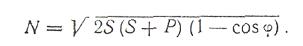
Натяжение S можно подсчитать по формуле
Таблица 1. Значения веса и махового момента некоторых употребительных шкивов
| D - диаметр шкива, м |
Р - абсолютный вес шкива, кг |
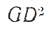-маховый момент шкива, кгм2 |
| 3.0 |
1950 |
9400 |
| 3.5 |
2320 |
14800 |
| 4.0 |
2800 |
24000 |
| 4.5 |
3270 |
37500 |
| 5.0 |
4000 |
56300 |
| 5.5 |
5300 |
85200 |
| 6.0 |
7400 |
115000 |
Значения дополнительной растягивающей силы оказываются незначительными по сравнению с основными силами. Это обстоятельство оправдывает приближенный метод определения X. В ряде случаев трение между втулкой и осью шкива оказывается настолько значительным, что сила X вообще будет отсутствовать.
При определении усилий, возникающих в канате в экстренные моменты его работы, влияние инерции шкива можно не учитывать.