 (1);
(1);Практической задачей создания оптимальных условий охлаждения слитка в зоне вторичного охлаждения (ЗВО) является установление количественных соотношений между коэффициентами теплоотдачи и плотностью орошения. Однако теоретический учет всех факторов, имеющих место при теплообмене в ЗВО, представляет собой сложно разрешимую задачу. Поэтому на практике используют определенные по эмпирической зависимости средние по поверхности коэффициенты теплоотдачи. Установлено, что эта зависимость имеет почти линейный характер и может аппроксимироваться следующим выражением [1,2].
 (1);
(1);
где:
 - плотность орошения,
- плотность орошения,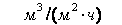 ;
;
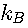 - коэффициент пропорциональности, определяемый из опыта,
- коэффициент пропорциональности, определяемый из опыта, .
.
По данным различных авторов для разных случаев
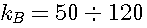 ,
, .
.
Линейная зависимость может использоваться в рабочих диапазонах изменения плотности орошения примерно до 20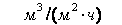 . При дальнейшем повышении величины плотности орошения значение коэффициента теплоотдачи примерно стабилизируется.
Приведенная выше методика расчета теплообмена в ЗВО удобна для практического использования, но она не позволяет учесть крайне неравномерное распределение коэффициента теплоотдачи, которое имеет место при водяном форсу ночном охлаждении высоконагретых поверхностей.
Разработка способов задания сложных граничных условий была проведена на Ново-Липецком металлургическом комбинате (НЛМК)[2] В.Л.Урбановичем в рамках проекта по всестороннему изучению работы МНЛЗ вертикального и радиального типа.
. При дальнейшем повышении величины плотности орошения значение коэффициента теплоотдачи примерно стабилизируется.
Приведенная выше методика расчета теплообмена в ЗВО удобна для практического использования, но она не позволяет учесть крайне неравномерное распределение коэффициента теплоотдачи, которое имеет место при водяном форсу ночном охлаждении высоконагретых поверхностей.
Разработка способов задания сложных граничных условий была проведена на Ново-Липецком металлургическом комбинате (НЛМК)[2] В.Л.Урбановичем в рамках проекта по всестороннему изучению работы МНЛЗ вертикального и радиального типа.
По способу охлаждения в ЗВО можно выделить несколько характерных зон поверхности:
-охлаждение на воздухе (излучением и конвекцией);
-контакт с роликом (брусом) [3];
-натекание струи воды, подаваемой форсункой;
-орошение стекающей водой за пределами действия факела форсунки.
Для первого участка локальное значение суммарного коэффициента теплоотдачи, учитывающего конвекцию и из лучение, выражали по формуле:
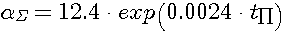
где:
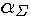 -локальный коэффициент теплоотдачи;
-локальный коэффициент теплоотдачи;
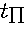 -локальное значение температуры поверхности слитка,
-локальное значение температуры поверхности слитка,
Значение эффективного коэффициента теплоотдачи на втором участке можно задавать по опытным данным, полученным для условий работы конкретных МНЛЗ. На третьем участке форсунки образуют области натекания струй в виде кругов (эллипсов). Распределение а в зоне натекания струи задается в виде экспоненциальной зависимости:
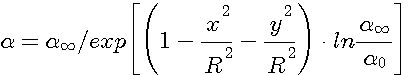 (2);
(2);
где х, у - координаты вдоль горизонтальной и вертикальной осей, м; R-радиус факела, создаваемого
форсункой на поверхности слитка, м; 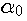 -коэффициент теплоотдачи в
центре факела,
-коэффициент теплоотдачи в
центре факела, ;
;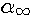 -коэффициент теплоотдачи на
границе факела,
-коэффициент теплоотдачи на
границе факела, ;
;
На четвертом участке коэффициент теплоотдачи принимали равным. Наличие на охлаждаемой поверхности в четвертой зоне устойчивой буферной паровой или паровоздушной пленки, изолирующей поверхность металла от потока воды, обуславливает сравнительно невысокие значения

 .
.
Для создания эффективной программы задания локальных коэффициентов теплоотдачи разработан метод разбиения сложной карты охлаждаемой поверхности на ряд простых карт. Значения а в каждой точке находили путем последовательного формализованного анализа простых карт. Для каждой из секций охлаждения вычисляли среднеинтегральные по площади коэффициенты теплоотдачи. Варьированием значения в центре зоны действия факела форсунки в уравнении (3) достигали совпадения средней величины коэффициента теплоотдачи по зоне со значением полученным по эмпирической зависимости (1).
Описанный выше подход является качественно новым шагом в решении указанной задачи. Однако, эта методика нуждается в усовершенствовании. Например, большую последовательность действий по подбору значения целесообразно заменить однозначным решением в виде последовательной цепочки действий без циклических возвратов и проверок выполнения условий сходимости. В данной работе предложена методика по изучению теплообмена в зоне вторичного охлаждения. Условие равенства средних значений коэффициентов теплоотдачи, полученных на основании расчетов по приведенной выше методике и рассчитанных по эмпирической зависимости (1), можно записать в виде следующего выражения:
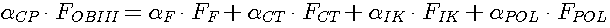 ;(3)
;(3)
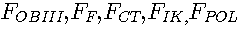 - площади исследуемого участка ЗВО, факелов форсунок, участка стекания охлаждающей воды, участка охлаждения за счет излучения и конвекции, контактного теплообмена с роликами соответственно, м2;
- площади исследуемого участка ЗВО, факелов форсунок, участка стекания охлаждающей воды, участка охлаждения за счет излучения и конвекции, контактного теплообмена с роликами соответственно, м2;
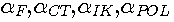 -средние коэффициенты теплоотдачи, от носящиеся к одноименным зонам,
-средние коэффициенты теплоотдачи, от носящиеся к одноименным зонам, .
.
Основой решения поставленной задачи является установление зависимости среднего для факела
коэффициента теплоотдачи от значений
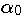 и
и
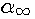 .
.
С математической точки зрения она сводится к решению уравнения:
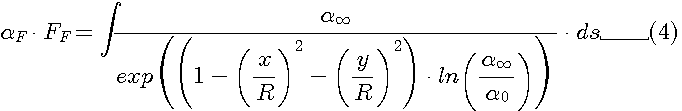 ;
;
Аналитическое решение уравнения (4) получено в следующем виде:
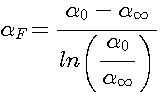 (5);
(5);
Подставляя решение (5) в выражение (3) и выполняя ряд преобразований, получим зависимость для определения коэффициента теплоотдачи в центре факела форсунки:
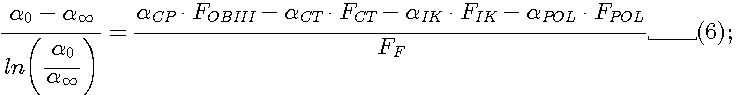
Полученное уравнение является трансцендентным. Для его решения необходимо воспользоваться одним из численных методов. Чтобы не разрабатывать программу по решению уравнения (6) самостоятельно, целесообразно воспользоваться вычислительным пакетом MathCAD. Для решения уравнений любого типа с одной переменной в нем предусмотрена функция Find(x). В этом случае решение любого уравнения представляется чрезвычайно простым.
В качестве примера использования данного метода исследования предлагается рассмотреть следующий пример. Заготовка сечением 150x150 мм находится на участке ЗВО, для, которого
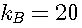 , a
, a 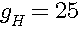 .
.
Необходимо рассчитать поле коэффициентов теплоотдачи для окрестности форсунки с радиусом факела 7,5 см. На исследуемом участке нет никаких опорно-поддерживающих устройств. Температура окрестностей углов слитка составляет 500 С. Схема расположения участков с различными закономерностями теплообмена на исследуемой поверхности приведена на рис. 1.
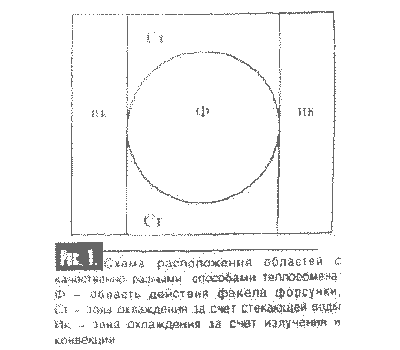
Для условий примера по описанной выше методике выполнен расчет полх коэффициентов теплоотдачи на участие поверхности слитка. Полученные результаты приведены на рис. 2.
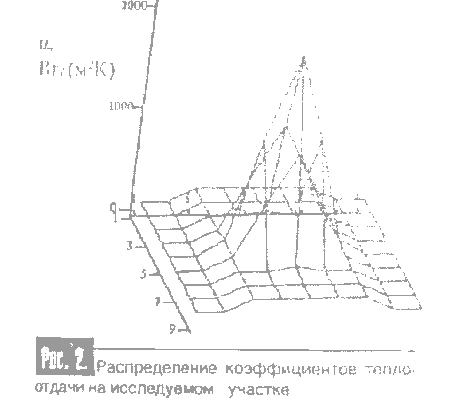
Где полученное поле представлено в виде поверхности. Предложенная в данной статье методика являемся значительным усовершенствованием методики, созданной В.Л. Урбановичем. Она позволяет глубоко исследовать закономерности теплообмена в ЗВО, является эффективным средством задания граничных условий в зоне вторичного охлаждения для математических моделей непрерывной разливки. Введение такого рода граничных условий позволит получать более точное распределение поля температур в формирующемся непрерывном слитке.
Литература
1. Непрерывная разливка стали на радиальных установках/В.Т. Сладкошеев, Р.В. Потанин, О.Н. Суладзе, В.С. Рутес. М.: «Металлургия», 1974.-288с.
2. Емельянов В.А. Тепловая работа машин непрерывного литья заготовок. Учебн. пособие для вузов.- М.: «Металлургия», 1988.-143с.
3. Дюдкин Д.А. Качество непрерывнолитой стальной заготовки. К.: Техника, 1988. – 253с.