Назад в библиотеку
«Динамическое проектирование самодвижущихся систем. Подвеска двигателя и структурные соединения»
Кафедра инженерной механики. Государственный университет Огайо, США. e-mail: singh.3@osu.edu
Автореферат. Динамические исследования и вибро-акустическое моделирование самодвижущихся конструкций представлены двумя случаями. Первый случай рассматривает роль и эффективность пассивных и адаптированных гидравлических двигательных опор. В то же время, важность сварных соединений, креплений корпуса тележки и устройства шасси с крепежными балками «Т» и «L» типа. В каждом случае были представлены аналитические и экспериментальные результаты. Нерешенные проблемы кратко обсуждались.
Ключевые слова. Динамическое проектирование, подвеска двигателя, структурные соединения, самодвижущаяся система, вибро-акустическое моделирование.
1. Введение
Двигатель, корпус и шасси самодвижущейся системы подвержены неуравновешенным движущим силам, неуравновешенным силам особенно на малых скоростях, динамические колебание в коробке передач и в других участках трансмиссии. По этому проектирование должно быть направлено на создание компактных и производительных самодвижущихся машин, отношение веса рамы двигателя сопоставимо с нарастанием интенсивности движущей силы. Следовательно, исследование и разработка должны бать сосредоточены на улучшении технологии подвески двигателя для достижений лучшей виброизоляции, плавного движения тележки и уменьшения шума. Такая проблема динамического проектирования представлена в виде исследования случая гидравлических опор. Представленные результаты математического моделирования и экспериментального исследования коротко обсуждались. Предложена новая адаптированная система подвески двигателя.
Динамика поведения сварных соединений, механическая связь сцепок тонколистовых стенок конструкции самодвижущейся тележки дает представление о данных для инженерных расчетов на изгибную и крутильную жесткость. Следовательно текущее исследование в значительной степени эмпирическое и основывается главным образом на конструктивном опыте и интуиции. Требования к проектированию для статических и динамических нагрузок имеют противоречия, как низкий уровень давления требует в соединениях жесткой связи, хотя исследования для низких уровней вибрации и шума требуют более податливых соединений. На практике, тем не менее, не аналитические инструменты проектирования пригодны для решения таких проблем. Более общий выбор инструментов для анализирования и динамических исследований необходимый для истолкования лучших существующих конструкций, улучшения общих основ нового или улучшенного процесса сваривания. Проблема формулируемая в этой статье с крепежными балками «Т» и «L» типа, как общий пример. Методики для определения жесткости соединений обсуждалась.
2. Предмет изучения. Гидравлические опоры
2.1 Понятие пассивной опоры.
Подвеска двигателя должна удовлетворять двум основным но противоречивым критериям. Первый должен жесткий и в большей степени демпфированного контроля малых вибраций и резонанс подвески двигателя достигает 5-30 Гц. Также должен быть способ контролировать и поглотить возможный удар, результат действия квази-статической нагрузки аналогична движению по неровной дороге, внезапные ускорения и замедления тележки, торможение и поворот. Второй, для малого возбуждения колебаний частоты высшего порядка применение податливой резиновой опоры (резинового гасителя) отвечающей требованиям виброизоляции и акустического комфорта. Обычный резиновый амортизатор не может удовлетворять одновременно двум требованиям как допустимые коэффициент жесткости kr и вязкого демпфирования br, волна сдвига почти постоянна с амплитудой колебаний и частотой 1-250 Гц. таким образом, компромисс между контролем резонанса и изоляцией неизбежен. Движение обычно оптимизируется для определения ориентировочных значений kr и br. Это удовлетворяет выполнению двух требований. Гидромеханическая опора созданная недавно и используется во многих транспортных средствах. На рисунке 1 схематически изображена гидромеханическая опора. Такое движение обеспечивает улучшение жесткостных и амортизационных характеристик, которые изменяют частоту и амплитуду колебаний, это концептуально лучшая пассивная опора известная в настоящее время.
2.2 Математическая модель пассивной опоры.
Типичные динамические свойства представлены на рисунке 2, где К - величина динамической жесткости, φk - произвольный угол, Х - начальная фаза. Аналитические расчеты также сравнивались с этим графиком, основная нелинейная модель описывается в статье (Singh et al 1992; Kim & Singh 1993, 1995). Разница между теоретическими и экспериментальными исследованиями 50 Гц.
На рисунке 3 представлена концептуальная модель которая включает в себя нелинейную модель и линейную опорную систему с коэффициентами жесткости kr и коэффициентом демпфирования, me и ms масса двигателя и масса подвески соответственно, u(ω,х) нелинейно зависящая от времени гидравлическая сила. Рисунок 4 сравнивает спектр амплитуд колебаний подпружиненной опоры с ускорением X"S(ω) и резиновую опору с гидравлической имеющую дросселирующую щель диаметром Δd = 0, 0.7 и1.4 мм. Пик резонанса достигает 9,2 Гц при слабом демпфировании резиновой опоры. Инерционность частей амортизатора с Δd = 0 ясно выражена динамической характеристикой с частотой до 15 Гц. нелинейная зависимость проявляется в амортизаторе с дросселирующей щелью Δd = 0.7 и 1.4 мм, когда взаимодействуют оба звена амортизатора. Придел может быть достигнуть частоты 15 Гц, тогда податливость верхней, жесткой, опоры велика. На самом деле резиновые опоры эффективно работают на высоких частотах. Дополнительная информация о нелинейных моделях амортизаторов и принципов колебательного силового потока освящен а статье(Singh et al 1992; Kim & Singh 1993, 1995, Roystan & Singh 1995-1997)
Динамическое проектирование самодвижущихся систем

Рисунок 1. Гидравлическая опора.
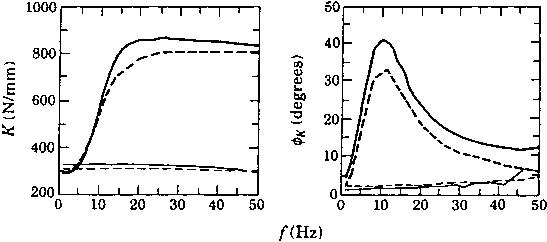
Рисунок 2. Типичные динамические характеристики гидравлических амортизаторов . Расчетный и экспериментальный спектр динамической жесткости простой опоры. (---- Теоретически для X= 1.0 мм; - экспериментально для X = 0.1мм; ---- теоретически для X = 0.1mm; - экспериментально для X = 1.0 mm.)
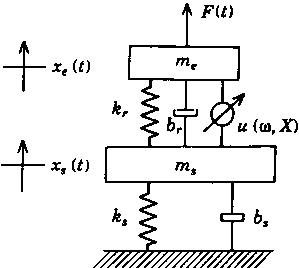
Рисунок 3. Динамическая модель гидравлической подвески двигателя.
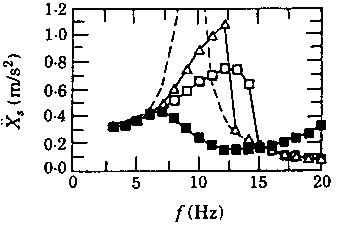
Рисунок 4. Сравнение обычных резиновых опор с гидравлическими амортизаторами. Моделирование частотных характеристик модели тележки для Fa = 100 Н. (Эффект дросселирующей щели X"S(ω); , Δd = 0мм; Δ, Δd = 0.7мм; Δ, Ad = 1.4 мм; - - - - резиновой опоры.)
Назад в библиотеку



