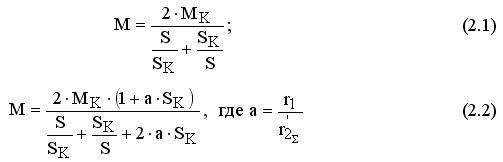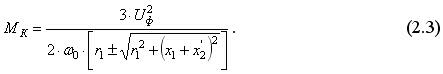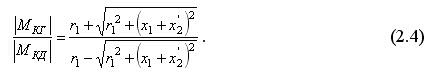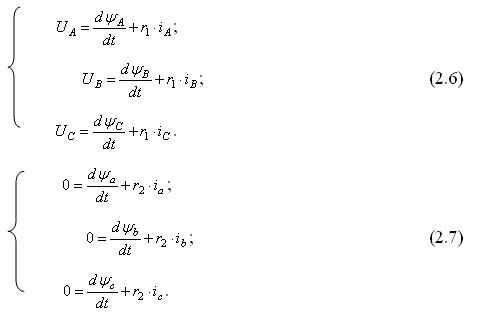Назад в библиотеку
2. Кондрахин В.П. докт. техн. наук., проф.,(ДонНТУ) - «Разработка математической модели электромеханической системы многодвигательного электропривода скребкового конвейера на базе двухскоростных асинхронных двигателей»
Математическая модель двухскоростного асинхронного электродвигателя.
До настоящего времени наиболее простым способом учета свойств приводного асинхронного двигателя было использование уравнения его механической характеристики в упрощенном или уточненном видах (рис. 1.1).
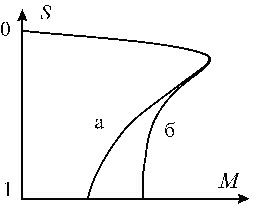
Рисунок 2.1.- Статические характеристики двигателя, построенные по формуле (2.1) - а), по формуле (2.2) – б).
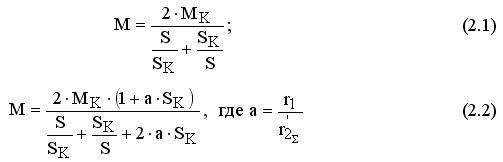
Применение для привода цепного конвейера двухскоростных асинхронных электродвигателей ставит вопрос о возможной работе двигателей в генераторном режиме при переходе на высокую скорость вращения.
Выражение для критического момента с учетом двигателя может быть записано в виде:
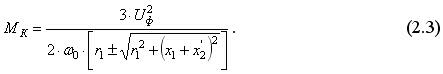
Знак «+» соответствует двигательному режиму, а «-» – генераторному. Если взять отношение абсолютных величин критического момента в генераторном режиме и в двигательном режиме, то из (2.3) получим:
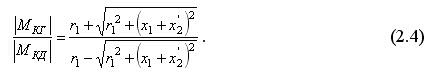
Критический момент двигателя в генераторном режиме превышает последний в двигательном режиме. Проф. Голован А.Т. приводил диапазон изменений этого отношения –
Практически, для большинства асинхронных машин это отношение может быть принято в районе 1,5. Пример характеристики в первом и втором квадрантах дан на рис. 2.2.
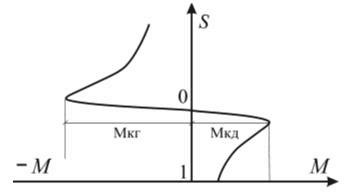
Рисунок 2.2 – Статистическая характеристика двигателя
Следует отметить, что эти значения даны без учета электромагнитных явлений в асинхронном двигателе. Если учесть электромагнитный переходной процесс в двигателе, то отношение MКГ/МКД может быть существенно выше 1,5.
Применение специальных двухскоростных асинхронных двигателей для привода скребкового конвейера ставит целый ряд вопросов, касающихся организации процесса разгона и выхода системы на режим установившегося вращения (движения конвейера с рабочей скоростью).
Для двухскоростного двигателя типовые электромеханические и механические характеристики имеют вид, представленный на рис. 2.3
Особо следует оговориться, что для применяемых приводных двигателей конвейеров в каталожных (паспортных) данных не приводится величина максимального (критического) момента для низшей (первой) скорости.
Переключение с малой скорости на большую (с первой на вторую) может сопровождаться возникновением нового переходного процесса, в частности, электромагнитного в двигателе и электромеханического – в системе. Примерный вид динамической механической характеристики при переключении с обмотки низкой скорости (ОМ) на высокую (ОБ) показан на рис. 2.4.
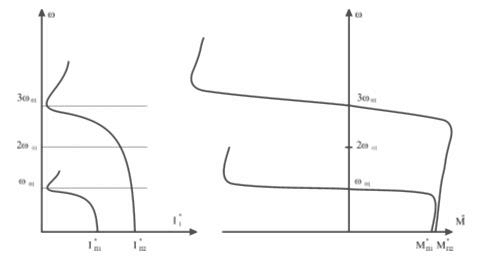Рисунок 2.3 – Электромеханические и механические характеристики двухскоростных двигателей
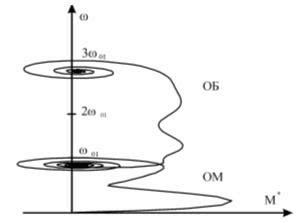Рисунок 2.4 – Динамическая механическая характеристика двигателя при переключении с ОМ на ОБ
Как видно из рис. 2.4, выбор момента переключения с ОМ на ОБ при наиболее благоприятном электромагнитном состоянии двигателя может способствовать снижению динамических нагрузок в элементах привода и системы.
Очевидно, что наиболее полное и всестороннее исследование поведения электромеханической системы (ЭМС) конвейера может быть проведено только при учете электромагнитных явлений в двигателе, а также при максимальном приближении расчетной схемы модели конвейера к реальной.
Для описания электромагнитных переходных процессов асинхронной машины, как и для любого электромеханического преобразователя энергии, необходимо составить уравнения электрического и механического равновесия, а также уравнение преобразования электромагнитной энергии в механическую. Первая группа уравнений представляет собой уравнения по первому закону Кирхгофа, записываемые для цепей каждой обмотки машины; второе – уравнение движения привода, а третье – устанавливает количественную связь, характеризующее преобразование электромагнитной энергии в механическую и наоборот.
При выводе дифференциальных уравнений асинхронной машины вводятся следующие допущения: не учитываются насыщение магнитопровода, потери в стали, а также влияние пазов; принимается, что фазовые обмотки выполнены одинаковыми, воздушный зазор равномерен; не учитываются высшие пространственные гармоники магнитного поля, т.е. магнитное поле каждой обмотки считается распределенным синусоидально по окружности расточки статора. Обычно также принимается, что параметры ротора приведены к цепи статора.
Асинхронный двигатель следует рассматривать как систему магнитосвязанных обмоток, расположенных на статоре и роторе.
Рассматривая взаимодействие обмотки фазы А статор и обмотки фазы а ротора, необходимо подчеркнуть, что взаимное положение этих обмоток в пространстве при вращении ротора непрерывно изменяется. С учетом принятых выше допущений взаимоиндуктивность между обмотками А и а может быть принята равной:
MAa=M12*cos(φAa) (2.5)
где М12 - максимальная величина взаимоиндуктивности, которая имеет место при совпадении осей обмоток А и а, Гн;
φAa - угол между осями обмоток фаз А и а, эл. рад.
Уравнения напряжения трех фаз статора и ротора имеют следующий вид:
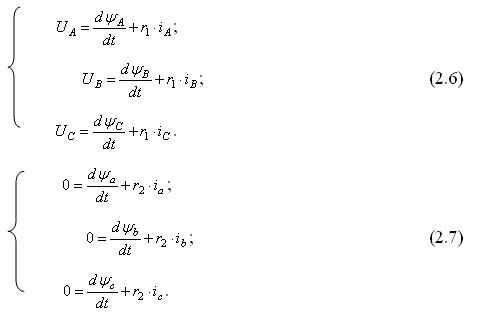
Окончательная система уравнений примет вид:
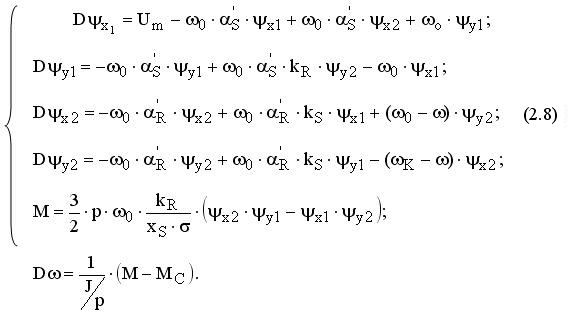
Данная система уравнений справедлива для одного фиксированного числа пар полюсов. При изменении числа пар полюсов необходимо переключить структуру модели с сохранением начальных электромагнитных величин (см. рис. 2.6).
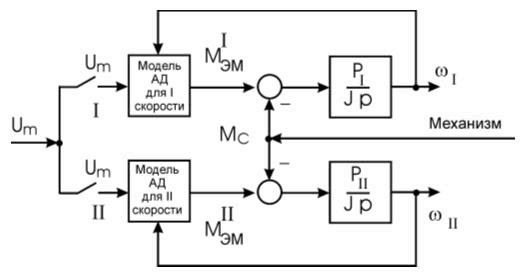Рисунок 2.7. – Блок-схема модели двухскоростного двигателя
Список источников.
1. Косарев В.В. Новая техника Донгипроуглемаша - основа интенсифи-кации добычи угля //Уголь Украины.-2003.№9.-С.5-9.
2. Скребковые конвейеры нового технического уровня. Андреев Г.В.,Косарев И.В., Лелека И.Т., Довженко В.И. // Уголь Украины.-2003.№9.-С. 36-38.
3. Стадник Н.И., Сергеев А.В., Мезников А.В. Система управления и привод забойных скребковых конвейеров // Уголь Украины.-2003.№9.-С. 38-41.
4. Скребковые конвейеры. Справочник / Под ред. А.В. Леусенко. - М.: Недра, 1992. – 221с.
Назад в библиотеку