Назад в библиотеку
3. Кондрахин В.П. докт. техн. наук., проф.,(ДонНТУ) - «Расчетные схемы, упругие, инерционные и диссипативные характеристики привода конвейера при наличии и отсутствии торсионного вала и упругой муфты»
Кинематическая схема редуктора привода конвейера КСД27 представлена на рис. 3.1
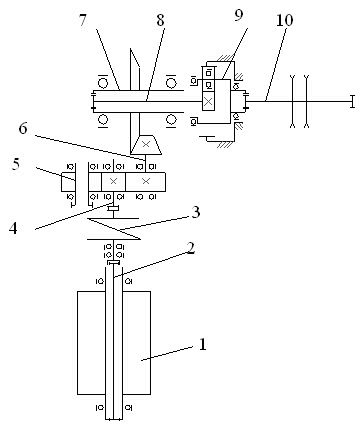
Рисунок 3.1 Кинематическая схема редуктора конвейера КСД27
На рисунке приняты следующая нумерация узлов и деталей, которая используется в дальнейшем при составлении расчетной схемы в качестве индексов при соответствующих динамических характеристиках: 1 – ротор электродвигателя; 2 – торсионный вал; 3 – упругая муфта; 4 – первый вал в сборе; 5 – вал храпового натяжного механизма в сборе; 6 – второй вал в сборе; 7 – третий вал в сборе; 8 – четвертый вал; 9 – планетарная передача; 10 – вал приводной звезды в сборе.
Массовые моменты инерции элементов привода определялись из их твердотельных моделей на компьютере и приводились к ротору двигателя путем деления момента инерции детали или сборочной единицы на квадрат передаточного отношения. Результаты определения инерционных характеристки приведены в таблице 3.1. Номера в первой колонке соответствуют обозначениям по рис. 3.1.
Таблица 3.1 – Массовые моменты инерции элементов привода, кгм^2
| Составной элемент
|
Момент инерции
|
Передаточное число
|
Приведенный момент инерции
|
| Ротор (1,2)
|
5,04
|
1
|
5,04
|
| Муфта (3)
|
0,783
|
1
|
0,783
|
| Вал (4)
|
0,117
|
1
|
0,117
|
| Вал (5)
|
0,285
|
1,39
|
0,148
|
| Вал (6)
|
0,347
|
2,278
|
0,067
|
| Вал (7,8)
|
11,1
|
5,84
|
0,323
|
| Водило (9)
|
14,8
|
33,4
|
0,013
|
| Вал звезды (10)
|
13,1
|
33,4
|
0,012
|
Из таблицы следует, что доля момента инерции ротора двигателя в общем моменте инерции привода достигает 78 %, другими динамически значимыми инерционными элементами являются упругая муфта (12%) и валы 7 и 8 с коническим колесом (5%).
Суммарные упругие характеристики привода конвейера определены экспериментально. Для составления расчетной схемы необходимо знать долю податливости каждого из элементов в общей податливости привода. Для определения этой доли был выполнен расчет податливости составных элементов привода по методике. Полученное общее расчетное значение коэффициента податливости привода примерно на 20 % меньше экспериментально полученного значения. Это обусловлено тем, что в расчете не учитывалась податливость корпусных деталей, подшипников и изгибная податливость валов.
Анализ результатов расчетного и экспериментального определения податливости показывает, что основными податливыми элементами редуктора (без учета торсионного вала и упругой муфты) являются вал 8 (28%), планетарная передача 9 (25%) и вал звезды 10 (46 %). С учетом полученных результатов построены расчетные динамические схемы привода конвейера КСД27 в линейной постановке, которые представлены на рис.3.2. Схема а) соответствует варианту привода без торсионного вала (Т) и упругой муфты (М), б) – с торсионным валом без упругой муфты, в) с торсионным валом и упругой муфтой; г) и д) - упрощенные универсальные расчетные схемы одного и двух приводов.
Параметры упрощенной расчетной схемы привода конвейера КСД27 приведены в таблице 3.2.
Таблица 3.2 - Приведенные к двигателю параметры расчетных схем
| Вариант привода
|
Jзв,
кгм^2
|
Jдв,
кгм^2
|
e, 10^-4,
1/Hм
|
ßc
Нмс
|
δ,рад
|
| M-T-
|
5,55
|
0,012
|
1,04
|
70
|
0,6
|
| M-T+
|
5,55
|
0,012
|
1,38
|
60
|
0,6
|
| M+T-
|
5,55
|
0,012
|
1,82
|
58
|
0,6
|
| M+T+
|
5,55
|
0,012
|
2,16
|
53
|
0,6
|

Рисунок 3.2 - Расчетные динамические схемы привода конвейера КСД27
Диссипативные свойства привода конвейера характеризует линеаризованный коэффициент сопротивления ?с, значения которого получены в соответствии с рекомендациями. При этом использовались также результаты построения гистерезисных петель при статическом нагружении приводов, в частности принято, что коэффициент поглощения системы с упругой муфтой на 12% выше, чем без муфты.
Как показали экспериментальные исследования, при пуске конвейера происходит изменение знака момента на валах редуктора, что сопровождается пересопряжением зазоров в соединениях и зубчатых передачах. Динамические исследования механических систем привода с зазорами, как правило, проводятся на основе кусочно-линейной модели. На расчетной динамической схеме зазоры обозначены символом δ. Величина δ представляет собой приведенный к звену приведения (к электродвигателю) суммарный зазор в соединении. Величина зазора в трансмиссии определяется по величине мертвого хода, который может быть найден как экспериментально, так и расчетным путем. Приведенные в таблице значения зазора получены методом параметрической идентификации в ходе вычислительных экспериментов с использованием разработанных математических моделей.
Список источников.
1. Косарев В.В. Новая техника Донгипроуглемаша - основа интенсифи-кации добычи угля //Уголь Украины.-2003.№9.-С.5-9.
2. Скребковые конвейеры нового технического уровня. Андреев Г.В.,Косарев И.В., Лелека И.Т., Довженко В.И. // Уголь Украины.-2003.№9.-С. 36-38.
3. Стадник Н.И., Сергеев А.В., Мезников А.В. Система управления и привод забойных скребковых конвейеров // Уголь Украины.-2003.№9.-С. 38-41.
4. Скребковые конвейеры. Справочник / Под ред. А.В. Леусенко. - М.: Недра, 1992. – 221с.
Назад в библиотеку


