Моделирование процессов нагрева металла является составной частью общей задачи построения автоматизированной системы управления нагревом металла. Оно позволяет изучать в широких пределах температурных диапазонов общие закономерности, присущие данному классу методических печей, а также рассматривать вопросы, связанные с определенной печью. Применение моделей нагрева для выбора наилучших технологических режимов позволяет значительно сократить объем экспериментальных работ, проводимых на обьекте, но, конечно не исключает и не заменяет их.

     В автоматизированной системе управления нагревательными печами назначение модели нагрева состоит в том, чтобы обеспечить систему информацией о температуре заготовок в текущий момент и о возможной траектории нагрева в будущем – в зависимости от предполагаемых условий нагрева.

     При разработке автоматизированной системы управления методическими печами к моделям нагрева металла предъявляют следующие требования:

     1. Модель должна обеспечить информацию о температуре металла с заданной точностью, исходя из выбранной цели управления.

     2. Заданная точность должна быть получена с наибольшей степенью простоты.

     3. Модель должна учитывать только те факторы, которые изменяются в процессе работы объекта.

     4. В процессе работы может произойти изменение параметров процесса нагрева в печи, поэтому необходимо автоматически подстраивать модель к этим изменениям.

     Для создания модели нагрева слитков в методической трехзонной печи наиболее приемлем классический метод - формирования уравнений модели на основе применения известных физических законов.

     Математическая модель, ориентированная на использование для разработки и настройки управления нагревом, должна учитывать: нагрев партий заготовок металла, причем каждая из заготовок должна при необходимости рассматриваться как массивное в теплотехническом смысле тело; окисление поверхности металла; потребление топлива по зонам в стационарных режимах печи. На рисунке 1 представлена структурная модель объекта моделирования.

     Выходная величина – температура металла , входная величина – температура печи . Теплообмен происходит по закону . Нагреваемая поверхность F; масса металла m, кг; удельная теплоемкость металла c, Дж/(кгС); коэффициент теплопередачи к поверхности металла , Вт/(м2С).

     Количество тепла, передаваемого металлу за время , равно:

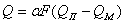
     Это тепло расходуется на изменение температуры металла на . Принимаем, что перепад температур внутри металла отсутствует.

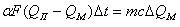
     Используя закон сохранения энергии, приравниваем полученное и израсходованное количества тепла:

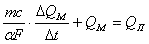
     откуда

     Переходя в предел при уменьшении к производной, получаем:

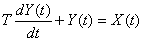
     В общем виде можно записать:

     Для получения передаточной функции слитка преобразуем дифференциальное уравнение (5).

     Введем замену:

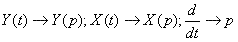
     тогда

     Следовательно, передаточная функция слитка имеет вид:

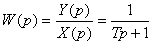
     Это апериодическое звено первого порядка с звеном запаздывания. Постоянная времени Т=230с, время запаздывания [2]

     Промоделировав в пакете Matlab структурную схему получили переходный процесс, показанный на рис. 2. Здесь видно, что полученный процесс не удовлетворяет поставленные требования к математической модели. Т.е в этом переходном процессе большое время запаздывания, перерегулирование, малое быстродействие, очень большое время моделирования. Поэтому следует усовершенствовать этот процесс.

     1. А.Г. Бутковский, С.А. Малый Управление нагревом металла. – М.: Металлургия, 1981, 272 с.

     2. З.Е. Круашвили Автоматизированный нагрев стали. – М.: Металлургия, 1973, 327с.