Применение кибернетического подхода для синтеза моделей развития социально-экономических объектов

Зотов В.А.
Источник:Доклады научных конференций Российской экономической академии им. Плеханова

Application of a cybernetic approach for the synthesis of development models of socio-economic objects. Zotov V.A.
Socio-economic objects belong to ones of cybernetic class. Their description with the aid of systems of dynamic nonlinear differential equations with nonstationary structure allows to synthesize adequate models and to get correct results of forecasting.

Впервые слово кибернетика (ciberne’tique) использовал знаменитый физик и математик А. М. Ампер как термин, определяющий науку об управлении государством (часть II труда “Essai sur la philosophie des sciences”, Paris, 1848). Вторую жизнь в 1948 г., но уже с несколько изменённым  смыслом, ему дал американский математик Норберт Винер, назвав кибернетикой созданное им новое научное направление. В настоящее время под кибернетической системой понимается система, обладающая обратными связями и динамическими элементами внутри себя. Исходя из указанной выше характеристики социально-экономические объекты, безусловно, можно отнести к системам кибернетического класса.

Модель сложного кибернетического объекта представляет собой структуру, состоящую из взаимосвязанных между собой объектов более низкого уровня.  То есть существует связь каких-то свойств. А это значит, что изменения, происходящие в любом из объектов более низкого уровня, всегда повлекут изменения других. Указанная связь между объектами может быть формализована в виде однозначно определённой функции-преобразователя. Таким образом, можно рассматривать модель кибернетического объекта как множество алгоритмов преобразований входных сигналов в выходные. Алгоритмы, описывающие динамику социально-экономических объектов, обладают рядом особенностей.

Во-первых, они должны иметь входные сигналы из внешней среды, то есть модель социально-экономического объекта не может быть рассмотрена как изолированная система. В качестве входов такой системы обычно моделируются различные экзогенные управления. В контексте социально-экономических объектов это могут быть регулирующие нормативные акты различных уровней власти. Например, бессмысленно моделировать динамику налоговых ставок иначе как через внешнее управление по причине их директивного изменения соответствующими структурами власти. Тем более что алгоритмы формирования ставок налогов до настоящего момента теоретически не разработаны.

Во-вторых, они должны обладать выходными сигналами. Причём часть из них служат индикаторами (показателями), другая – эндогенными сигналами управления для динамических алгоритмов на следующий квант модельного времени.

В-третьих, большинство сложных объектов, к которым относятся  социально-экономические объекты, относятся к классу объектов с нелинейными элементами. Отсюда, модель, описывающая этот объект, должна описываться нелинейными уравнениями. Любое его описание с помощью линейных уравнений является грубым отражением реального объекта, которое в очень редких случаях может использоваться для упрощения и только тогда, когда проявляющиеся при нелинейности свойства являются незначительными для результатов исследования.

Помимо отмеченных выше особенностей, алгоритмы должны носить строго детерминированный характер, то есть не иметь вероятностных элементов. По причине того, что социально-экономический объект является сложным и динамическим по своей природе, а взаимосвязи между его параметрами непрерывно меняются как качественно, так и количественно  по всему  временному континууму (нестационарность структуры), одинаковое управление, но в разные моменты времени (экзогенное и эндогенное), приведёт к различным и непредсказуемым последствиям. Это порождается постоянным изменением порога чувствительности алгоритмов к входным сигналам. Отмеченная особенность приводит к тому, что управление может привести в ряде случаев к крайне нежелательному развитию процесса, например, банкротству. Алгоритмы, основанные на стохастическом математическом аппарате, в отличие от детерминированных,  не позволят повторить эксперимент в точности при таких же условиях и выявить исходную причину катастрофы, которая может находиться задолго до неё.

Модели сложных социально-экономических объектов часто имеют большую размерность и требуют то количество стартовой информации, сбор которой или невозможен в принципе по причине отсутствия статистических наблюдений, или займёт неприемлемо длительное время. Применение кибернетического подхода в разы уменьшает количество необходимой для инициализации начальных условий модели информации.

Можно рассматривать экономическую деятельность людей как процесс создания (переработки), накопления и перераспределения ресурсных потоков (рис.1).

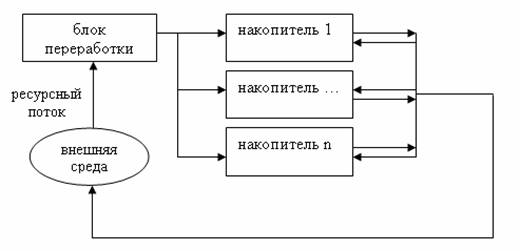
Рис. 1. Агрегированная схема экономической деятельности

При таком подходе к анализу экономической динамики, оперирующим ресурсными потоками, становятся не менее важными, чем  просто объём передаваемых ресурсов, такие факторы как:
а) время поступления ресурсов;
б) интенсивность потока;
в) пропускная способность канала, проводящего ресурс;
г) инерционность блока переработки ресурса (блока-преобразователя);
д) чувствительность блока-накопителя.

Именно кибернетический подход позволяет не только алгоритмизировать с учётом вышеуказанных свойств логику функционирования подавляющего большинства социально-экономических объектов, но и сделать механизм алгоритмизации лучше теоретически обоснованным  по сравнению с другими.

С учётом данных требований для синтеза динамических моделей сложных социально-экономических объектов предлагается использовать математический аппарат нелинейных дифференциальных уравнений. Модель реального объекта описывается системой таких уравнений с переменными коэффициентами. То есть коэффициенты при параметрах дифференциальных уравнений сами являются результатами решения этой же системы уравнений и также могут описываться нелинейными дифференциальными уравнениями. По этим причинам  появляется большое дополнительное количество обратных связей. Всё это: нелинейность преобразований и наличие обратных связей,  в конечном счёте, приводит к нестационарности всей структуры модели во временном континууме. Количество обратных связей в модели сопоставимо с количеством параметров. Причём в процессе моделирования отдельные обратные связи могут менять свой характер,  поменять свой знак на противоположный (с отрицательного на положительный и наоборот), перестать действовать («заснуть»), или, наоборот, активизироваться («проснуться»). Привнесением нестационарности в моделируемую систему достигается бо'льшая адекватность модели её реальному эквиваленту. Однако нестационарность налагает и ряд ограничений. Так, например, неверные начальные условия в модели неминуемо приведут её в процессе моделирования к разрушению.

Для описания элементов динамической модели используется математический аппарат теории автоматического регулирования (ТАР). Данная теория была разработана для создания систем автоматического управления (САУ). Эти системы характеризуются тем, что без непосредственного участия человека способны поддерживать необходимый режим работы различных обслуживаемых объектов. «САУ самостоятельно, без вмешательства извне либо поддерживают постоянными, либо изменяют по заданным законам одну или несколько физических величин, характеризующих процессы, происходящие в обслуживаемых объектах, или же сами определяют в зависимости от ряда условий нужный или оптимальный закон управления объектом»[1]. Моделируя социально-экономические объекты, мы имеем огромное количество как эндогенных, так и экзогенных рычагов управления. Причём необходимо осуществлять непрерывное управление этими рычагами на всём модельном времени. Оператор-человек не способен управлять столькими рычагами одновременно. Поэтому управление частью из них доверяется автоматам. Для такого управления в контур вносится стабилизированный параметр-норма. Автомат стремиться асимптотически приблизить значение автоматизированного рычага управления к значению нормы. Норма же в свою очередь, являясь неким коэффициентом, как было уже отмечено ранее, может постоянно менять своё значение в процессе моделирования под воздействием как экзогенных, так и эндогенных факторов. Управление в данном случае принимает форму регулирования. Методология, отработанная в ТАРе, как  нельзя лучше помогает моделировать такое управление.

В соответствии с нотацией, принятой в теории автоматического регулирования, модель формализуется в виде структурных схем, описывающих взаимосвязи между различными компонентами (блоками) исследуемой системы. Структурная схема состоит из звеньев. Каждое звено представляет собой динамический (интегрирование, запаздывание, взятие реальной производной и др.) или статический (суммирование, тригонометрические функции, логарифмирование и др.) оператор преобразования. Оператор характеризуется функцией преобразования входного сигнала в выходной, коэффициентом передачи, частотной, фазовой характеристиками.

Описанный выше кибернетический подход для синтеза моделей и прогнозирования динамики процессов в социально-экономических объектах позволяет:
а) корректно формализовать модели реальных объектов;
б) в интуитивно-понятной форме синтезировать модели посредством    операторов, чья   функция  переходного процесса редко имеет степень свободы большую двух;
в) за незначительное время прогнозировать развитие процесса описываемого     дифференциальным уравнением с порядком, доходящим в ряде случаев до нескольких сотен.
Таким образом, его применение в динамическом моделировании является не только оправданным, но и принципиально корректным.

 

1. Егоров. К. В. Основы теории автоматического регулирования, учебное пособие для вузов, изд. 2-е, переработан. и доп., М, «Энергия», 1967. 648 с. с илл.
2. Сб. «Философские проблемы кибернетики», Соцэкгиз, М., 1961, стр. 155-156.
3. Цянь-Сюэ-Сень. Техническая кибернетика, под редакцией А. А. Фельдбаума, изд-во иностранной литературы,  Москва, 1956.

4. Норберт Винер. Кибернетика или управление и связь в животном и машине, изд. 2-е, «Советское радио», Москва, 1968.