РАССПОЗНАВАНИЕ ИСКУССТВЕННЫМИ НЕЙРОННЫМИ СЕТЯМИ ГРАФИЧЕСКИХ ОБРАЗОВ ПРИ НАЛИЧИИ ИСКАЖЕНИЙ В РЕАЛЬНОМ ВРЕМЕНИ
Махно Ю.С., Федяев О.И.
Донецкий национальный технический университет
Тезисы доклада на III международную научно-техническую конференцию молодых учёных и студентов «Информатика и компьютерные технологии 2007». В докладе основной раскрываемой темой является, за счет чего достигается быстрота распознавания, а также устойчивость к искажениям при использовании неокогнитрона.
Проблема эффективного распознавания образов имеет важное значение в сферах автоматизации многих процессов человеческой деятельности, связанных с идентификацией различных объектов окружающего мира, например, авторизация рабочего персонала по отпечаткам пальцев или сетчатке глаза, идентификация продукта и расчет цены в магазине по штрих-коду, слежение за автомобилями въехавшими на территорию по их номерам и т. д. Все эти действия должны выполнятся моментально, чтобы не останавливать рабочий процесс.
В настоящее время одним из эффективных способов распознавания является подход на основе искусственных нейронных сетей (ИНС). В результате последних медицинских исследований появилась возможность смоделировать искусственную нейросеть, структура которой базируется на строении зрительной коры головного мозга. Модель этой сети – названная неокогнитроном – показала высокую эффективность её применения для распознавания образов, подверженных различным искажениям.
С технической точки зрения неокогнитрон является иерархической нейронной сетью состоящей из достаточно большого числа слоев идущих друг за другом и имеющий неполные (можно даже сказать достаточно редкие) связи между слоями [2]. Входной образ подается на входной слой и далее передается каждому последующему. Слоевая структура неокогнитрона показана на рис. 1.

Рисунок 1 – Структура неокогнитрона
Неокогнитрон состоит из двух типов слоев: простые и комплексные. Нейроны входящие в простые слои настраиваются на распознавание каких-либо определенных образов. Комплексные же матрицы созданы для того, чтобы объединить однотипные результаты распознавания простых матриц. Рассмотрим пример объединения результатов распознавания на базе двух шаблонов для первого слоя, каждый из которых представляет собой отрезок, наклоненный на 22 градуса от горизонтали (см. рис. 2, 3).

Рисунок 2 – Шаблоны распознавания
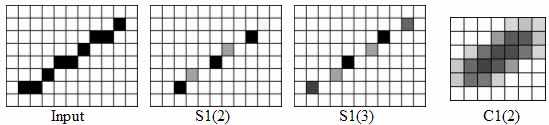
Рисунок 3 – Пример объединение результатов распознавания
Еще одной особенностью неокогнитрона является то, что он обучается слой за слоем, это позволяет ввести достаточно большое количество слоев и обучить их за непродолжительный отрезок времени. Довольно часто в неокогнитроне пользуются 8 слоями (4 простых и 4 сложных слоя [1, 3, 4]) с приблизительным количеством в 15000 нейронов. Использование такого количества нейронов и слоев, например, в сети обратного распространения ошибки привело бы к очень долгому (почти невозможному) обучению нейронной сети.
Каждый нейрон как простого, так и комплексного слоя получает сигналы не от всех нейронов, а лишь от некоторых, что также влияет на увеличение скорости распознавания образов неокогнитроном. Такие нейроны называются «областью видимости» [1]. Размерность областей видимости может быть различна, однако в результате исследований было выявлено, что оптимальные размеры областей видимости это 3х3 и 5х5. Для центрального нейрона каждой матрицы, центральный элемент области видимости располагается в центре матрицы предыдущего слоя (см. рис. 4).
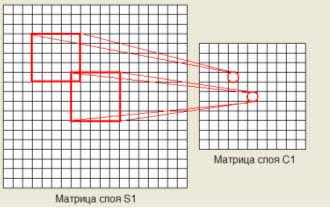
Рисунок 4 – Области видимости
Различают слои со сжатием и без него. Для слоев со сжатием характерно то, что размерность его матриц меньше, чем размерность матриц предыдущего слоя. Для сжатия могут использоваться различные методы. В создаваемой модели для слоев со сжатием используется следующий метод: центр области видимости нейрона, смещенного на 1 позицию от центрального нейрона, смещается на 2 единицы относительно центра матрицы предыдущего слоя (см. рис. 5). Для примера приведенного на рисунке 4 получается, что в область видимости угловых элементов входят только 4 нейрона.
У нейронов, расположенных в матрицах слоев без сжатия, индекс центрального элемента области видимости соответствует его индексу в матрице. В неокогнитроне не все коэффициенты являются настраиваемыми, также имеются фиксированные коэффициенты, расчет которых производится в самом начале моделирования. Настраиваемыми коэффициентами в неокогнитроне являются коэффициенты от нейронов комплексного слоя к нейронам простого слоя и коэффициент от подавляющего нейрона к нейрону простого слоя. Коэффициенты от комплексных нейронов к подавляющему нейрону и от простых нейронов к комплексным являются фиксированными. В связи с этим возникает проблема выбора фиксированных коэффициентов. Изначально, предполагается лишь, что значения коэффициентов должно уменьшаться при удалении от центра области видимости. При настройке весовых коэффициентов используется простая формула расчета Δ, которая зависит от величины входных сигналов (с): Δwi,j = a * ti,j * ci,j; wi,j(k+1) = wi,j(k) + Δwi,j[3], здесь t – фиксированные коэффициенты от комплексных нейронов к тормозящему нейрону, и a – скорость обучения. Величина Δ, для весового коэффициента подавляющего нейрона выбирается так, чтобы процесс обучения мог завершиться. В проделанной работе выбрана следующая формула: Δw0 = a * v / 2.
Таким образом, неокогнитрон, являясь универсальным средством для распознавания графических образов, имеет такие важнейшие качества как быстрая скорость обучения и распознавания образов, расширяемость модели, для получения более точных результатов распознавания. Эти качества позволяют использовать эту нейронную сеть для распознавания образов в реальном времени.
Литература
- Lauren Fausett. Fundamentals of Neural Networks: Architectures, Algorithms and Applications. New Jersey: Prentice Hall 398-417 pp. 2000.
- Ф. Уоссермен. Нейрокомпьютерная техника. Теория и практика. М.: Мир, 1992 – 260 с.
- S. Satoh, J. Kuroiwa, H. Aso and S. Miyake. Recognition of Hand-written Patterns by Rotation-invariant Neocognitron Proc. of ICONIP'98, 1, pp. 295-299, 1998.
- S. Satoh, J. Kuroiwa, H. Aso and S. Miyake, Pattern Recognition System with Top-Down Process of Mental Rotation, Proc. of IWANN'99, 1, pp. 816-825, 1999.