ПОВЫШЕНИЕ КАЧЕСТВА РАСПОЗНАВАНИЯ СЦЕН НЕЙРОННОЙ СЕТЬЮ «НЕОКОГНИТРОН»

С.В. Аксёнов, В.Б. Новосельцев
Институт «Кибернетический центр» при ТПУ

Изложены базовые принципы обучения и использования нейронной сети «Неокогнитрон». Показаны особенности модификаций неокогнитрона, инвариантного к вращению и с переменной селективностью. Предложены варианты расширения данной парадигмы для уменьшения избыточности сети.

Идея неокогнитрона впервые была предложена Фукушимой в [1–4] как универсальная система распознавания двумерных образов. Считается, что организация работы неокогнитрона наиболее близка к процессам, происходящим в зрительной коре головного мозга человека. К главному достонству системы можно отнести её нечувствительность к позиционным сдвигам, масштабированию и зашумлениям анализируемого образа. Процесс классификации разбивается на этапы, каждый из которых характеризуется анализом содержательно различных признаков, но выполняется согласно общей процедуре. На каждой стадии обработки происходит выделение существенных свойств выходов предыдущей стадии и формирование сжатого представления этих свойств для следующего этапа обработки. Важно подчеркнуть, что на любом текущем шаге в качестве входных используются только данные, являющиеся выходом предыдущего шага. На рис. 1 приведена иллюстрация поэтапного функционирования неокогнитрона.

Рисунок 1 – Этапы иерархического извлечения свойств неокогнитроном

Каждая стадия обработки выполняется фиксированными слоями неокогнитрона. Первоначальный слой нейронной сети носит название входного или рецептивного. Послойная обработка образа выполняется до тех пор, пока не будут найдены его меры сходства со всеми классами, известными сети.

Нейронные клетки соединены между собой посредством передаточных устройств – синапсов, которые, помимо прочего способны усиливать либо гасить сигнал. Можно сказать, что все знание о запоминаемых объектах, накапливаемое в процессе обучения сети, сконцентрировано в величинах силы передачи синапсов между нейронными клетками. В отличие от полносвязных моделей нейронных сетей, в которых все нейроны текущего слоя соединены со всеми нейронами предшествующего слоя, в неокогнитроне нейроны соединены только с определенной областью нейронов предыдущего слоя, называемой областью связи. Каждый слой нейронной сети состоит из непересекающихся фрагментов, называемых плоскостями нейронов. На наш взгляд термин «плоскость» не совсем удачен, но мы будем его употреблять, учитывая его традиционность. Плоскость нейронов – это область, состоящая из нейронов, обрабатывающих соседние фрагменты анализируемого образа, и служащая для распознавания или сжатия информации.

В состав неокогнитрона для распознавания входит несколько видов нейронных клеток, а именно простые (S-клетки) и сложные (С-клетки). Эти клетки составляют плоскости соответственно простых (S-) и сложных (С-) плоскостей. Основная задача простых плоскостей – производить извлечение существенных характеристик. Каждая S-плоскость обучена так, чтобы реагировать на определенный входной вектор. S-плоскости разбиты на пересекающиеся области – области конкуренции. В каждой области конкуренции, после возбуждения плоскости, определяется нейрон с максимальным значением выходного сигнала, выходы же остальных нейронов из этой области становятся равным нулю. Такой эффект носит название бокового или латерального торможения. Вообще говоря, торможение – процесс влияния одного нейрона на другой с целью уменьшения выходного сигнала последнего, целью процесса возбуждение напротив является увеличение выходного сигнала нейрона, на который производится воздействие.

Каждая S-клетка из простой плоскости на вход получает вектор из областей связей сложной плоскости предыдущей стадии. Набор весовых коэффициентов синапсов, соединяющих область связи и каждую S-клетку одинаков для всех S-клеток, находящихся в одной S-плоскости. Это гарантирует, что существенные характеристики объекта будут обнаружены вне зависимости от их расположения на входной плоскости клеток. C-клетка последующей сложной плоскости активируется (выдает сжатое приближение), если активна хотя бы одна S-клетка, входящая в область связи данной С-клетки.

Заключительный этап обработки реализуется алгоритмом «победитель забирает все» – среди всех выходов сети выбирается максимальный, соответствующий наиболее похожему из запомненных классов.

Помимо S- и C-клеток в состав неокогнитрона входят тормозящие V-клетки. Если С-клетки служат для возбуждения S-клеток, то V-клетки служат для торможения последних. Выходом V-клетки служит среднее значение выходных сигналов сложных нейронов, попадающих в область связи. Следует заметить, что каждой S-клетке соответствует одна V-клетка, причем их области связи одинаковы. Все синапсы в нейронной сети принадлежат одному из следующих классов:

1. модифицируемые возбуждающие: al(v,p,k) – используются для возбуждения S-клетки из рецептивных областей C-клеток, здесь и ниже l – номер слоя, k – номер плоскости, v – расположение синапса внутри области связи, p – номер С-плоскости, в которой располагается связь;
2. немодифицируемые возбуждающие: cl(v) – используются для активации V-клеток из областей связи C-клеток, dl(v) – для возбуждения C-клеток из рецептивных полей S-клеток и el(t,n,k) – при латеральном торможении S-клеток внутри областей конкуренции, где t – расположение синапса внутри области конкуренции между нейронами;
3. модифицируемые тормозящие: bl(k) – используются для торможения активности S-клеток активностью соответствующей V-клеткой;
4. немодифицируемые тормозящие: el(t,n,k) – используются при латеральном торможении S-клеток внутри областей конкуренции.

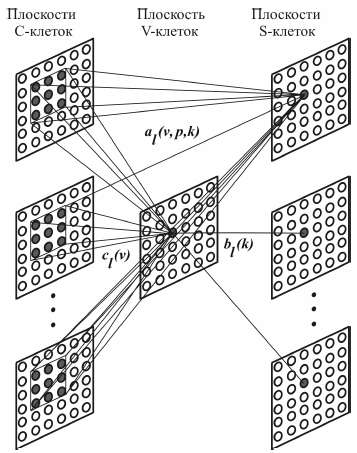
Рисунок 2 – Связи между нейронами слоев плоскостей C-, V- и S-клеток

На рис. 2 представлен пример связей между C-, V- и S-клетками. Темные клетки в плоскостях C-клеток попадают в область связи выделенных S-клеток и служат для возбуждения отмеченной на рисунке тормозящей V-клетки.

После попадания образа на входной слой неокогнитрона последовательно возбуждаются слои из простых и соответствующих им сложных плоскостей. Выход S-клетки на позиции n в k-той плоскости слоя l вычисляется как

где A_l – область связи соответствующей S-клетки, r_l – параметр селективности (степень близости входного сигнала и сигнала, которому были научены синапсы клетки), функция φ(...) есть пороговолинейная функция:

Выход оказывающей тормозящее действие на соответствующие ей S-клетки V-клетки на позиции n слоя l описывается выражением:

K_Cl – количество С-плоскостей в слое l.

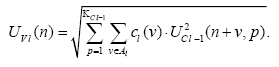
Плоскости S-клеток делятся на перекрывающиеся области конкуренции, внутри этих областей обучается только один нейрон, обладающий максимальным значением выходного сигнала. Подавление активности нейронов-соседей в области конкуренции происходит методом латерального торможения, аналогичного используемому в нейронной сети MAXNET [5]. Чтобы избежать длительной итеративной процедуры исключения слабейших выходов в [6] предложена модель ускоренного латерального торможения (рис. 3).

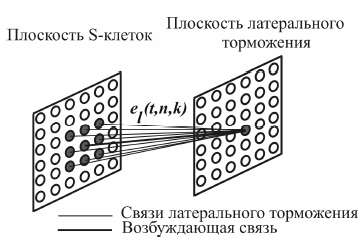
Рисунок 3 – Ускоренное латеральное торможение

Выход нейрона на позиции n плоскости k слоя l латерального торможения описывается формулой:

Значения весов тормозящих синапсов области конкуренции берутся из расчета:

где I_l – область конкуренции внутри слоя l. После извлечения свойств и определения нейрона-победителя в каждой области конкуренции происходит активация сложных плоскостей. Выход С-клетки на позиции n в k-той плоскости слоя l выражается как:

где D_l – область связи соответствующей C-клетки, j(p,k) – число связности p-тoй S-плоскости и k-той С-плоскости. (Фукушима [1] предполагал величину j(p,k) равной 1). Функция ψ(...) определяется как:

Пример соединения плоскости латерального торможения и плоскости сложных клеток приведен на рис. 4.

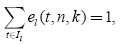
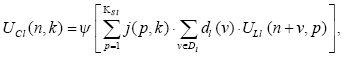
Рисунок 4 – Пример соединения плоскости латерального торможения и сложной плоскости

Весовые коэффициенты a_l(v,p,k) и b_l(k) в начале обучения устанавливаются близкими нулю и далее вычисляются в процессе обучения неокогнитрона. Значения остальных весовых связей берутся следующим образом:

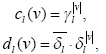, где γ_l > 0; δ_l <= 1; δ_l > 0;

Как уже отмечалось выше, настройке подлежат значения весов a_l(v,p,k) и b_l(k). После определения нейрона-победителя в каждой рецептивной области производится настройка его весов:

, где

m – номер обучающего образа, q_l – коэффициент скорости обучения.

К сожалению, данная модель нейронной сети не способна к правильному определению образа, если последний был повернут на угол, превышающий 30° (тестировалось на выборке из печатных букв). Для того, чтобы создать структуру, инвариантную к вращению образа, в работах [7, 8] была предложена модель, основанная на стеках плоскостей клеток. Двумерный вариант нейронной сети (положение образа по осям X и Y) был изменен на трехмерный (добавился угол поворота образа относительно запомненного вектора). При прохождении сигнала по сети S-/C-клеток, плоскость, находящаяся на вершине стека, получает входной вектор без изменений. На вход последующей в стеке плоскости S-/C-клеток поступает тот же вектор, но умноженный на матрицу вращения на определенный угол поворота, заданный проектировщиком сети (нами был взят угол 25°). На вход третьей плоскости – образ с углом поворота 25°+25° = 50° и т. д. В работе [7] показано, что при наличии стеков плоскостей с углами поворота 90, 180 и 270° нейронная сеть способна безошибочно распознавать 85,3% образов символов против 76,2% образов, опознанных классическим неокогнитроном.

Графическое представление модели стеков плоскостей представлено на рис. 5.

Рисунок 5 – Структура неокогнитрона, инвариантного к вращению образов. Примечание: US1, US2, US3 – слои S-плоскостей, UC1, UC2, UC3 – слои C-плоскостей, U0 – входной слой

Дальнейшим расширением способности к распознованию этой нейронной сети является регуляция параметра селективности r_kl. В работе Гильдебрандта [9] разработан алгоритм настройки данного параметра. Основная идея алгоритма Гильдебрандта состоит в том, чтобы производить регуляцию селективности S-клеток, при этом области связи в разных S-плоскостях были как можно больше без взаимного перекрытия. После обучения вектор весов S-клетки al становится пропорционален вектору суммы входных обучающих векторов: U_Cl–1,1+U_Cl–1,2+U_Cl–1,3+... Практически [10] данный метод определяет селективность клетки на основе усредненных обучающих характеристик. Таким образом, метод Гильдебрандта не гарантирует, что среди всей обучающей выборки не найдется вектора, не попадающего в требуемую область связи, рис. 6.

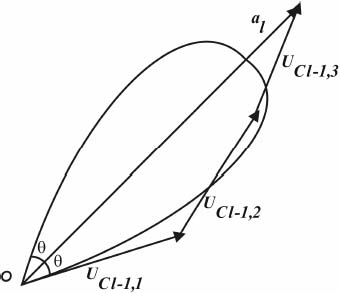
Рисунок 6 – Пример непопадания обучающего вектора (в данном случае U_Cl–1,1) в область связи с селективностью r_kl, соответствующей углу θ

Значения отклика S-клетки при её активации векторами U_Cl–1,1, U_Cl–1,2 и U_Cl–1,3 равны соответственно 0, длине вектора OB и длине вектора OC (рис. 7).

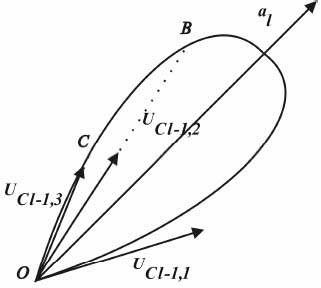
Рисунок 7 – Определение значения отклика S-клетки при её возбуждении тремя обучающими векторами после обучения

Одним из решений отмеченной проблемы обучающей выборки может стать настройка селективности, при котором гарантируется минимальный отклик S-клетки на все обучающие образы U_{Sl min}. Основанный на такой настройке метод называют «близкое к оптимуму обучение, основанное на характеристике» (Sub-Optimal Feature-based Training, SOFT) [11–13]. Параметр _{Sl min} выбирают в пределах от 0 до 1.

В [12] показано, что изменение селективности r_kl разумно производить, первоначально настраивая весовые коэффициенты слоя, а затем модифицируя селективности. Таким образом, первоначально инициализируется начальное значение селективности r_kl и значение минимального отклика клетки min(X_Sl(k)), затем производится активизация слоя m-тым обучающим вектором, и, если активация клетки победителя в области конкуренции X_Sl(n_klm,k) меньше текущего минимума отклика, производится обновление текущего минимума на величину активации победителя, т. е. если X_Sl(n_klm,k) < min(X_Sl(k)), то min(X_Sl(k))=X_Sl(n_klm,k). После предъявления всех обучающих образов начинается настройка параметра селективности r_kl:

Рис. 8 наглядно иллюстрирует изменение рецептивной области по сравнению с ситуацией, показанной на рис. 7. Ясно, что в последнем случае все обучающие вектора попадают в требуемую рецептивную область. Заметим, что при этом происходит и увеличение значений выхода клетки при возбуждении векторами U_Cl–1,2 и U_Cl–1,3.

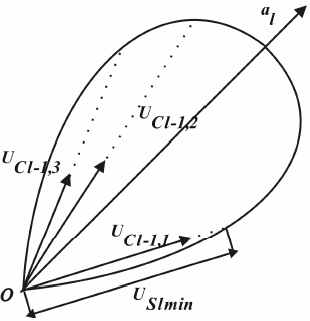
Рисунок 8 – Уменьшение селективности рассматриваемой S-клетки

При данном обучении может случиться, что все вектора U_Cl–1,j приблизительно равны, тогда селективность рецептивной области примет вид узкого лепестка (высоко селективная клетка). Если же на вход клетки поступит сигнал, значительно отличающийся от остальных, то селективности нейронов существенно уменьшатся. Пример изменения селективности клеток представлен на рис. 9. Селективность клеток № 2 и 3 увеличилась, а клетки № 1 – уменьшилась.

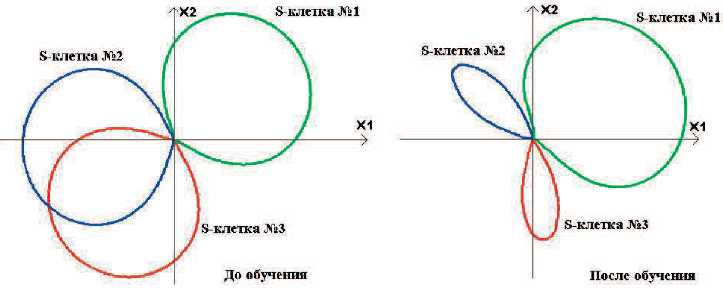
Рисунок 9 – Пример изменения селективности

Представленные результаты служат основой для дальнейших исследований по повышению эффективности неокогнитрона. Далее планируется провести работы в двух направлениях. Первое – построение расширенной иерархической модели на основе уже обученной сети. Второе направление – замена стека плоскостей, отвечающих за реагирование на вращение образа, на рекурсивную модель обработки входного вектора в слое, когда каждая последующая стадия сравнения с эталонами начинается, если не нашлось похожего образа с тем же углом, при этом производится изменение соответствующего параметра входного образа. Предполагается также распространить предложенный подход на родственные классы задач прогнозирования и контроля. Таким образом, проведен анализ нескольких вариантов при построении систем иерархического извлечения свойств. Предложены подходы по дальнейшему расширению возможностей существующих моделей на основе использования уже запомненных системой знаний.

Литература

1. Fukushima K. Neocognitron: A Self-Organizing Neural Network model for a Mechanism of Pattern Recognition Unaffected Shift in Position // Biological Cybernetics. – 1980. – № 4. – P. 193–202.
2. Fukushima K. Analysis of the Process of Visual Pattern Recognition by the Neocognitron // Neural Networks. – 1989. – № 2. – P. 413–420.
3. Fukushima K. Neocognitron: A Hierarchical Neural Network Capable of Visual Pattern Recognition // Neural Networks. – 1988. – № 1. – P. 119–130.
4. Fukushima K. Neocognitron for Handwritten Digit Recognition // Neurocomputing. – 2003. – № 51. – P. 161–180.
5. Lippman R. An Introduction to Computing with Neural Nets // IEEE ASSP Magazine. – 1987. – № 4. – P. 4–22.
6. Fukushima K. Cognitron: A Self-organizing multilayered neural network // Biological Cybernetics. – 1975. – № 2. – P. 121–136.
7. Satoh S., Kuroiwa J., Aso H., Miyake S. Recognition of Hand-written Patterns by Rotation-invariant Neocognitron // 5th Intern. Conf. on Neural Information Processing. – Tokyo, 1998. – № 1. – P. 295–299.
8. Satoh S., Kuroiwa J., Aso H., Miyake S. Pattern Recognition System with Top-Down Process of Mental Rotation // 5th Intern. Work- Conference on Neural Network. – Alicante, 1999. – № 1. – P. 816–825.
9. Hildebrandt T.H. Optimal Training of Threshold Linear Correlation Classifiers // IEEE Transactions on Neural Networks. – 1991. – №2. – P. 577–588.
10. http://svr-www.eng.cam.ac.uk/~drl/Publications/Publications.html
11. Lovell D.R., Downs T., Tsoi A.C. A Note on a Closed-Form Training Algorithm for the Neocognitron // IEEE Transactions on Neural Networks. – 1993. – № 2. – P. 367–368.
12. Lovell D.R., Downs T., Tsoi A.C. An Evaluation of the Neocognitron // IEEE Transactions on Neural Networks. – 1997. – № 8. – P. 100–105.
13. Lovell D.R., Downs T., Tsoi A.C. Is the Neocognitron Capable of State-of-the-art Digit Recognition? // IEEE Transactions on Neural Networks. – 1995. – № 1. – P. 94–97.