1. Введение в динамическое ценообразование

1.1 От фиксированного ценообразования к динамическому

          Существует тенденция в ценообразовании, которая обещает значительно изменить способ маркетинга и продажи товаров. Продавцы теперь предлагают специальные сделки, подготовленные для индивидуальных клиентов, и начинают рассчитывать соответствующую цену для каждого клиента в необходимое время. Это изменение произошло в значительной степени из-за развития связей в экономике с помощью Интернета, корпоративных сетей и беспроводных сетей. Покупатели сейчас способны быстро и легко сравнивать товары и цены, выбирая лучшую позицию для заключения сделки. В то же самое время технология позволяет продавцам собирать детализированные данные о привычках и предпочтениях покупателей, даже рассчитать максимально допустимую стоимость покупки, таким образом они могут привести в соответствие свои товары и цены. В прошлом были значительные затраты, связанные с изменяющимися ценами, известные как стоимость прайсов. Для компании с большой производственной линией ценовое регулирование могло занимать месяцы, чтобы дойти до дистрибьюторов, розничных продавцов и коммивояжёров. Появление сетевой технологии уменьшило стоимость прайсов и время почти до нуля. Когда покупатели и продавцы перешли в электронный мир, полученные в результате этого динамические цены более близко отражают истинную рыночную стоимость товаров и продаваемых услуг.
          В заключение, выделяют два события в электронном бизнесе, которые привели к изменению парадигмы от фиксированного ценообразования к динамическому:
           1. Операционные затраты для осуществления динамического ценообразования были уменьшены за счет устранения потребности в людях, которые физически должны присутствовать в определенное время на определенном месте, сокращения затрат на поиск и сокращения затрат на составление прайсов для информирования об изменении цен.
          2. Рост нестабильности и изменчивости спроса привел к увеличению числа клиентов, числа конкурентов и количества информации. Само динамическое ценообразование приводит к увеличению ценовой нестабильности, и компании пришли к выводу, что использование единственной постоянной цены на этих изменчивых Интернет-рынках неэффективно и невыгодно.

1.2 Определение динамического ценообразования

          Динамическое ценообразование — это динамическое регулирование цен для потребителей в зависимости от ценности, которую эти клиенты приписывают товару или услуге. В литературе несколько альтернативных терминов использовались для описания динамического ценообразования. Они включают гибкое ценообразование и настраиваемое ценообразование. Динамическое ценообразование включает два аспекта: ценовая дисперсия и ценовая дискриминация. Ценовая дисперсия может быть пространственной или временной. В пространственной ценовой дисперсии несколько продавцов предлагают данный товар по различным ценам. Во временной ценовой дисперсии данный магазин изменяет цену данного товара в течение определенного времени в зависимости от времени продажи и ситуации требования поставки. Другой аспект динамического ценообразования — отличительное ценообразование или ценовая дискриминация, где различные цены назначают различным потребителям одного и того же товара. Выделяют три типа ценовой дискриминации:
          Первая степень (или совершенная) дифференцирования: производитель продает различные единицы продукции по различным ценам, и эти цены могут отличаться для разных людей. В этом случае каждая единица товара продана тому человеку, который оценивает ее наиболее высоко, по максимальной цене, которую этот человек готов заплатить за товар. Если производитель владеет достаточной информацией, которая определяет максимальную готовность заплатить для каждого клиента, этот метод способен помочь привлечь всех потребителей целевого сегмента рынка.
          Вторая степень ценового дифференцирования: ее также называют нелинейным ценообразованием, она означает, что производитель продает различные единицы продукции по различным ценам, но каждый человек, который покупает одинаковое количество товара, платит одинаковое количество денег. Таким образом, цены зависят от количества купленного товара, а не от того, кто делает покупку. Примеры включают количественные скидки и премии. Другой пример — предприятия коммунального обслуживания; например, цена за единицу электричества часто зависит от количества купленного электричества.
          Третья степень ценового дифференцирования: это происходит, когда производитель продает товары различным людям по различным ценам, но каждая единица товара, проданного данному человеку, продается по одинаковой цене. Ценовое дифференцирование достигается за счет различия в оценках потребителей. Пример — групповое ценообразование (пожилые люди, студенты и т.д.). Другой пример — телекоммуникационное ценообразование (отличительное ценообразование для фирм и домашних хозяйств). Часто ценовое дифференцирование достигается с помощью дифференцирования товаров. Последнее достигается за счет дополнительных признаков или при обобщении существующих признаков. При дифференцировании товаров продавцы могут уменьшить взаимозаменяемость их товаров и услуг и привести предлагаемую продукции в соответствие с требованиями определенных потребителей или сегментов рынка. Непосредственный пример — компания Dell Computers, где каждый продаваемый компьютер уникален, потому что он обладает уникальным набором свойств, выбранных каждым покупателем. Другой пример — авиационная промышленность, где товары дифференцированы на основе политики возмещения, отмены ограничений, оставшихся выходных и т. д.

1.3 Модели, используемые в динамическом ценообразовании

          Множество математических моделей использовалось для вычисления динамических цен. Большинство из этих моделей формулирует проблему динамического ценообразования как проблему оптимизации. В зависимости от определенного математического инструмента, используемого ими, авторы статьи предлагают список из пяти категорий моделей:
          Модели на основе ассортимента — это модели, в которых решения относительно ценообразования, прежде всего, основаны на уровнях ассортимента и уровнях обслуживания клиента.
          Модели управления данными — это модели, которые используют статистические или подобные методы для того, чтобы сделать доступными используемые данные о предпочтениях клиента и для покупки образцов, необходимых для вычисления оптимальных динамических цен.
          В моделях теории игр продавцы могут конкурировать за одну и ту же группу клиентов, и это вызывает игру динамического ценообразования среди продавцов. Теоретические модели игр приводят к интересным способам вычисления оптимальных динамических цен в таких ситуациях.
          В моделях, изучающих механизмы, рынок электронной коммерции представляет собой богатую область для изучения онлайн покупателей и продавцов. Продавцы могут потенциально изучить предпочтение покупателя и покупку образцов и использовать алгоритмы для динамического ценового предложения для максимизации доходов и прибыли.
          Имитационные модели, использующие моделирование, могут помочь решить любую проблему принятия решений. Имитационная модель для динамического ценообразования может использовать любую из четырех вышеупомянутых моделей или использовать систему опытного образца или любой другой способ имитации динамики системы.
          Вышеупомянутый способ для распределения на категории динамических моделей ценообразования не является окончательным. Классификация является ни взаимно исключающей, ни абсолютно исчерпывающей. Конкретная динамическая схема ценообразования может включать два или больше из вышеупомянутых типов. Данный тип модели может использовать другой тип. Например, модели на основе ассортимента могли быть данными для модели управления. Моделирование, изучающие механизмы, может быть основой для модели управления данными. Модели, изучающие механизмы, могут использовать уровни ассортимента в их изучающих алгоритмах и т. д. Моделирование уместно для всех других типов моделей. В этой статье авторы провели краткий обзор моделей на основе ассортимента, моделей управления данными, моделей теории игр и моделей, изучающих механизмы. В статье также представлен детальный пример, описывающий использование самообучающихся моделей для динамического ценообразования в электронной коммерции. Моделирование не рассматривается как отдельная тема, так как оно характерно для всех перечисленных моделей.

2. Использование самообучающихся моделей для динамического ценообразования на рынке электронной коммерции

          В этом разделе авторы представляют подход на основе самообучения для динамического определения цен на электронном рынке с единственным розничным продавцом. Отдельно авторы описывают метод для расчета оптимальных нелинейных динамических цен при стохастических требованиях, чувствительных к цене клиентоах и пополнении ассортимента.
          Авторы рассматривают единственного продавца магазина розничной торговли (типа amazon.com), который продает определенный товар и использует нелинейное ценообразование для различного размера покупки с целью поощрения покупки большого объема. Делая разумные предположения на основе политики продавца относительно ассортимента, времени пополнения склада и процесса прибытия клиентов, авторы используют марковскую модель для описания динамики этой системы. В этой модели состояния соответствуют ценам, предлагаемым продавцом для различных количеств купленного товара. Без потери целостности рассматривается ситуация, где магазин объявляет цены за одну единицу, две единицы и три единицы товара.
          При этом продавец может использовать самообучающиеся стратегии для динамического моделирования цен, чтобы максимизировать выбранный показатель. В качестве такого показателя выбрана долгосрочная регулируемая средняя прибыль. Продавец использует Q-изучение для определения оптимальной динамической политики ценообразования.
          Авторы описывают модели и методологию, которые могут использоваться для обеспечения принятия управленческих решений, таких как определение оптимального количества и времени повторного заказа.

2.1 Описание системы

          Авторы рассматривают розничный магазин, который назначает нелинейные цены для различных количеств товара. Розничные магазины таких товаров, как одежда, DVD, пища, напитки и т.д., являются непосредственными примерами. Представьте, что электронный розничный магазин объявляет: "Большие скидки за различные размеры покупки". Предполагается, что розничный магазин предлагает три типа покупок: одной единицы, двух единиц и трех единиц продукции. Клиенты различаются по объему их покупок (1, 2 или 3) как тип 1, тип 2 и тип 3 соответственно. Кроме того, если требуемый товар отсутствует, магазин принимает заказ и обещает доставить его прибывшему клиенту, и клиенты ждут товар, если предложение для них приемлемо. Делаются следующие предположения о динамике системы:
          Клиенты попадают в магазин по закону распределения Пуассона с нормой λ. По прибытию клиент смотрит на показанное меню и сам выбирает размер покупки. Предполагается, что прибывший клиент имеет тип 1 (то есть, решает купить только одну единицу) с вероятностью f1, тип 2 (то есть, решает купить две единицы) с вероятностью f2 и тип 3 (то есть, решает купить три единицы) с вероятностью (1 — f1 — f2). Фактически это означало бы, что прибытие клиентов типа c (c = 1, 2, 3) происходит по распределению Пуассона с нормой fi λ, где f3 = 1 — f1 — f2.
           Продавец поддерживает ограниченный ассортимент товаров. Imax — максимальная вместимость ассортимента в магазине продавца. Продавец следует стандартной политике при пополнении ассортимента: всякий раз, когда количество ассортимента (текущая норма ассортимента в розничном магазине плюс количество пунктов, заказанных как пополнение) снижается до уровня меньшего, чем r (называемого точкой повторного заказа), он заказал бы пополнение в размере (Imax — r). Отметьте, что это тонкая вариация классической (q; r) политики относительно ассортимента, с q = Imax и стохастическим временем пополнения.
          Когда число требуемых товаров приводит к увеличению времени ожидания клиентов и выходу этого времени за предел, скажем N, продавец применяет политику контроля входной платы и отклоняет клиентов до того времени, пока соответствующие пополнения не будут сделаны, и количество товаров, ожидаемых клиентами, не станет меньше, чем N.
          В любое данное время t, продавец использует правило ценообразования, которое гласит: цена pc для клиента типа c. Продавец считает цену p1 базисной ценой. Продавец выбирает p2 (p3) следующим образом. Сначала равномерно распределенный ценовой ряд выбирается для p2 (p3) за счет выбора верхних и нижних пределов для равномерного распределения таких, как p1b2min и p1b2max (p1b3min и p1b3max), где b2min, b2max (b3min, b3max) являются ценовыми ограничениями для выбора p2 (p3). Базисная цена p1 динамически изменяется продавцом в зависимости от окружающей среды. Главная проблема в том и состоит, чтобы продавец так выбирал p1 в ответ на события в системе, чтобы максимизировать свою прибыль? Время главного пополнения (время между размещением заказа пополнения и прибытием товаров) распределено экспоненциально (с математическим ожиданием 1/μ).
          Если товара нет при прибытии клиента типа c, клиент сможет узнать текущую цену pc и ожидаемое время получения товара. Если текущая цена за единицу и время поставки будут приемлемы для него, то прибывший клиент перейдет к покупке и останется. Иначе прибывший клиент оставляет систему без покупки. Мы можем предположить, что равномерное распределение описывает приемлемый ценовой ряд (C c min; C c max) для клиентов типа c, и второе равномерное распределение описывает приемлемый временной ряд поставок (D c min; D c max) для клиентов типа c. Основываясь на этих двух распределениях, текущей указанной цене и указанном времени поставок, можно легко определить вероятность того, что прибывший клиент типа c, который не находит никаких товаров в розничном магазине, останется в нем.
           Предполагается, что время поставки w, установленное продавцом для всех клиентов, всегда равно среднему времени пополнения, то есть 1/ μ. Это предположение оправдано политикой ассортимента, которую мы используем. Прибывший клиент типа c измеряет полезность оценки цены pc и оценки времени поставки w по формуле:

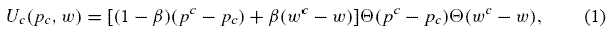
          где θ(x)= 1 если x >= 0 и 0 иначе, и 0 <= β <= 1. p c ≈ U(0; p cmax] и w c ≈ U(0; w cmax] с U(.), обозначающее равномерное распределение на указанном интервале для данных pmax и wmax.
           Если клиенты многократно используемых типов товаров конкурируют за товары, продавец выберет клиента каждого типа с равной вероятностью. Когда клиент прибывает в систему, определенное время требуется для получения ее оценок и решения, остаться ли ему или оставить систему. Предполагается, что это время незначительно. Можно предположить, что бесконечная очередь к серверу моделирует этот процесс, однако это не объясняет поведение системы лучше. Как только товар становится доступным, предполагается, что ждущий клиент немедленно заберет его, следовательно время на оплату и упаковку незначительно мало. Продавец имеет конечное число возможных вариантов для выбора базисной цены p1.
           Продавец берет на себя стоимость хранения ассортимента HI per за единицу товара в единицу времени и стоимость невыполнения заказа Hq per за единицу товара в единицу времени. Стоимость покупки единицы продукции — C. Стоимость заказа предположительно является незначительной. В этом примере продавец является обучающимся агентом. Каждый раз, когда клиент остается или оставляет систему, продавец может изучить окружающую среду, наблюдая за реакцией клиентов на динамическое изменение цены. Если клиент типа c решает остаться, продавец получит вознаграждение pc. Расходы продавца включают: стоимость покупки заказанных товаров, стоимость хранения ассортимента товаров и затраты невыполнения заказа для товаров, которые ожидают клиенты. В связи с этим продавец может динамически изменить базисную цену p1 для достижения оптимального значения. Полученная оптимальная цена помогла бы оценить выбранный показатель деятельности розничного магазина. В этой статье рассматрены два показателя эффективности деятельности магазина: общая долгосрочная дисконтированная прибыль и периодически получаемая прибыль в единицу времени.

2.2 Самообучающаяся модель динамического ценообразования

          Рисунок 2 изображает розничный магазин, описанный в предыдущем разделе. Очередь c — виртуальная очередь, содержащая ожидающих клиентов типа c. Из-за предположений о процессе прибытия и пополнения ассортимента модель марковского процесса для описания динамики системы наиболее целесообразна. Основа системы представлена кортежем (x1; x2; x3; I), где xc — число ждущих клиентов типа c в очереди c и I — норма ассортимента в розничном магазине. Возможный набор изменения цены, лежащий в основе системы — набор A, из которого продавец может выбрать цену p1 (p2 и p3 вычисляются на основе p1). Предполагается, что цены изменяются только при переходе из одного состояния в другое. Нетрудно заметить, что динамика системы и регулирования цен соответствуют динамике Марковского процесса.
Рисунок 2. — Модель розничного магазина с тремя группами клиентов
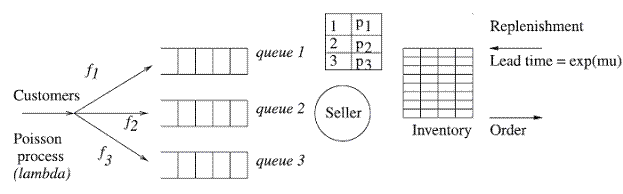
          Самообучающиеся методы считаются мощными для решения задач с использованием марковских процессов. Самообучающаяся модель ожидает сигнал поддержки от окружающей среды, который указывает правильность хода решения. Марковский процесс является инструментом для использования самообучающихся моделей. Продавец здесь является естественным обучающим агентом. Клиенты разделены на тип 1, тип 2 и тип 3 естественным способом, и продавец может быстро идентифицировать их. Продавец может видеть длину очереди. Он также знает средний размер оплаты при входе или выходе клиентов. Размер оплаты служит сигналом поддержки для используемой самообучающейся модели.

2.3 Динамика системы

          Очередь c на рисунке 1 в розничном магазине является виртуальной очередью для клиентов типа c. Пусть X (t): = (X1 (t); X2 (t); X3 (t); I (t)) будет основой системы у розничного продавца с Xc (.), представляющее количество зарегистрированных ранее запросов в очереди c и I (.), норма ассортимента у розничного продавце во время t. Розничный продавец назначает цену за единицу (p1) и оптовую скидку на своей веб-странице (цены p2 и p3) и может изменить цены только во время перехода из одного состояния в другое, что всякий раз происходит при покупке и уменьшении ассортимента или при регистрации запроса в любой из очередей. Клиент типа c купит товар или сделает заказ с предварительной регистрацией, когда Uc в (1) положительна. Легко заметить, что ценовая динамика может быть смоделирована как непрерывный марковский процесс.
          Во время 0 процесс X(t) наблюдается и классифицируется как одно из состояний в возможном наборе состояний S. После идентификации состояния розничный продавец выбирает способ ценообразования из списка A. Если процесс находится в состоянии i, и розничный продавец выбирает p1 є A, то процесс перейдет в состояние j є S с вероятностью Pij при условии, что следующее состояние будет j, время до следующего перехода является случайной переменной с вероятностным распределением Fij(p1).
          После перехода в новое состояние розничный продавец снова будет выбитать способ ценообразования, и все действия повторятся. Далее в состоянии i для выбранной цены p1 получаемый продавцом доход будет Sp(.), стоимость ассортимента будет H(i) и стоимость невыполнения заказа C(i; j), затраты будут следующие: пусть i = [x1; x2; x3; i1] и j = [x`1 ; x`2; x`3; i`1], тогда

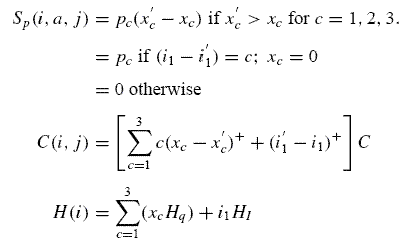
           Пусть p1 — это базисная цена продавца в наблюдаемом состоянии. Тогда происходят следующие переходы:
           [0; x2; x3; i1]→ [0; x2; x3; i1?1] с нормой f1λP(U1.(p1; 1/μ) > 0) для каждого x2; x3 и i1
           [0;0; x3; i1] → [0; 0; x3; i1 ? 2] с нормой f2λP (U2 (p2; 1/μ) > 0) для каждого x3 и 2 <= i1 < 3
           [0;0;0; i1] → [0; 0; 0; i1 ?3] с нормой f3λP(U3 (p3; 1/μ) > 0) для каждого i1 >= 3
           [x1; x2; x3; 0] → [x1 C 1; x2; x3; 0] с нормой f1λP(U1 (p1; 1/μ) > 0) для каждого x2; x3
           [x1; x2; x3; 0] → [x1; x2 C1; x3; 0] с нормой f2λP(U2 (p2; 1/μ) > 0) для каждого x1; x3
           [x1; x2; x3; 0] → [x1; x2; x3 C1; 0] с нормой f3λP(U3 (p3; 1/μ) > 0) для каждого x1; x2.

2.4 Ожидаемое среднее вознаграждение при долговременном управлении

          Пусть π: S → A обозначают стационарную детерминированную политику ценообразования, которой следует розничный продавец, выбирающий способ только на основе информации о состоянии системы. Пусть t0 = 0 и {tn}n >= 1 является последовательностью точек перехода между состояниями π и Х(tn-), которые обозначают состояния системы перед tn. В этом случае оценка ожидаемой долговременной регулируемой средней прибыли, начиная с состояния i для состояния π, составит:

          Задача розничного продавца состоит в том, чтобы найти π*: S → A по формуле:

          Предполагается, что s — специальное состояние, которое является текущим в цепи Маркова для каждого состояния. В последовательности состояний выделяются отдельные циклы, чтобы каждый из этих циклов мог рассматриваться как траектория состояния соответствующей стохастической максимизирующей прибыль функции цели с состоянием s в качестве последнего состояния. Для любого скаляра λ рассмотривается стохастическая максимизирущая прибыль функция цели с ожидаемой прибылью на стадии Σj Pij (p)[Sp(i; p; j) — C(i; j) — H(i)] — λ для всех i. Если зафиксировать ожидаемую прибыль стадии, полученную в состоянии i на уровне Σj Pij (p)[Sp(i; p; j) — C(i; j) — H(i)/] — λ*, где λ* является оптимальной средней прибылью стадии в состоянии s, тогда связанная стохастическая максимизирущая прибыль функция цели становится эквивалентной начальной средней прибыли в функции цели для данной стадии.
          Уравнение Беллмана имеет вид:

          где λ* является оптимальной средней прибылью на стадии и h*(i) интерпретируется как относительная прибыль для каждого состояния i по сравнению со специальным состоянием s.

2.5 Эксперимент моделирования

          Авторы моделируют и изучают работу модели розничного магазина, показанного на рисунке 2, рассматривая набор цен А = {8*0; 9*0; 10*0; 10*5; 11*0; 11*5; 12*0; 12*5; 13*0; 13*5}. Максимальная длина очереди для клиентов типа 1, 2 и 3 предположительно равна 10. Это означает, что в розничном магазине не может находиться более 10 клиентов любого типа одновременно. Максимальная норма ассортимента Imax предположительно равна 20 с точкой повторного заказа r = 10. С этими значениями параметров полученная модель марковского процесса имеет 161 состояние. Считается, что f1 = 0*4; f2 = 0*3. Приход клиентов в магазин происходит по распределению Пуассона со средним временем между прибытиями 15 минут. Верхние и нижние пределы равномерного распределения которое описывает приемлемый диапазон цен для клиентов типа 1, предположительно равны 8 и 14 соответственно. Эти пределы предположительно равны 12 и 24*5 для клиентов типа 2 и 18 и 35 для клиентов типа 3. Верхние и нижние пределы для равномерного распределения, которое описывает приемлемый диапазон времени поставки предположительно равны 0 часов и 12 часов соответственно. Авторы рассматривают время пополнения для повторных заказов со средним значением 3 часа. Стоимость хранения (HI) выбрана 0*5 за единицу в день и стоимость невыполнения заказа (Hq) выбрана 8*0 за невыполненный заказ в день. Предполагается, что продавец купил товары по стоимости 4 за единицу. Долговременная регулируемая прибыль в единицу времени используется в качестве показателя эффетивности деятельности розничного магазина.

Резюме

          Интернет и технологии электронной коммерции открыли богатые возможности для получения выгод от динамического ценообразования. Количество компаний, использующих динамические стратегии ценообразования, стремительно увеличивается. Кроме того испытываются все более и более сложные динамические стратегии ценообразования.
          В статье показано, что парадигма фиксированного ценообразования переходит к парадигме динамического ценообразования на рынках электронной коммерции, и что динамические стратегии ценообразования в случае должного использования выигрывают у стратегий фиксированного ценообразования. Авторы определили различные сроки и ключевые слова, используемые в контексте динамического ценообразования, и представили классификацию стратегий динамического ценообразования. Авторы определили условия, при которых стратегии динамического ценообразования будут лучше стратегий фиксированного ценообразования. В статье преставлены классифиция и обсуждение модели динамического ценообразования для четырех видов: модели на основе ассортимента, модели управления данными, модели на основе аукциона и модели, изучающие механизмы.
          В этой публикации описана роль самообучающихся методов для динамического ценообразования, и рассмотрена модель розничного магазина с одним продавцом при нелинейном ценообразовании для различных количеств покупаемого товара. Из этой статьи следует, что рынки электронной коммерции готовы к динамическому ценообразованию, и для определения оптимальных цен могут использоваться как более сложные экономико-математические модели, так и более простые динамические методы.

---