C. Valens, Guide to wavelet transform
Перевод выполнен Шаховой И. А. Ссылка: http://pagesperso-orange.fr/polyvalens/clemens/wavelets/wavelets.html
-
Введение
-
Непрерывное вейвлет-преобразование
-
Свойства вейвлета
-
Дискретные вейвлеты
-
Частотный фильтр
-
Интермеццо
-
Масштабирующая функция
-
Субполосное кодирование
-
Дискретное вейвлет-преобразование
-
Выводы
-
Ссылки
Всем известно, что Фурье представляет сигнал, заданный во временной области, в виде разложения по ортогональным базисным функциям (синусам и косинусам), выделяя таким образом частотные компоненты. Однако данное преобразование обладает некоторыми недостатками.
Недостаток Фурье анализа в том, что он обладает разрешением по частоте, но не имеет разрешения по времени: можно определить какие частоты присутствуют в сигнале, но невозможно определить, когда они в нем появляются. Это объясняется тем, что Фурье-преобразование представляет собой разложение сигнала на сумму функций, который перекрывают собой всю временную ось.
Решением проблемы является разбиение сигнала на части и анализ их по отдельности, но это приводит к обратной проблеме - наличию разрешения по времени, но потере разрешения в частотной области.
Проблема объясняется принципом Хэйзинберга, который утверждает, что невозможно знать точно частоту и точное время присутствия этой частоты(появления ее) в сигнале - сигнал не может быть представлен как точка в частотно-временном пространстве.
Недавно появившимся решением является вейвлет-анализ, в котором используется масштабируемое окно, передвигаемое по всему сигналу с расчетом спектра для каждой его позиции. Процесс повторяется множественно с изменением размера окна для каждого нового цикла. Такой подход называется многомасштабным анализом.
В вейвлет анализе частотно-временное пространство заменяют на масштабно- временное пространство. Чем больше масштаб, тем меньше различимы детали сигнала, таким образом, масштаб обратнопропорционален частоте сигнала.
Подход, представленный во введении известен под именем непрерывное вейвлет-преобразование. Формула преобразования имеет вид:
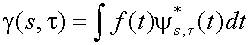 (1)
(1)
* означает комплексное сопряжение. Базовые функции
 называются вейвлетами. Выражение
(2) - запись обратного вейвлет-преобразования.
называются вейвлетами. Выражение
(2) - запись обратного вейвлет-преобразования.
Вейвлеты генерируются из начальной функции
 (t),
материнского вейвлета, методом масштабирования и сдвига.
(t),
материнского вейвлета, методом масштабирования и сдвига.
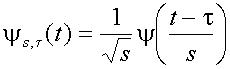 (3)
(3)
В (3) s - коэффициент масштабирования, коэффициент s-1/2 вводится для нормализации энергии сигнала при разных масштабах.
Важно отметить, что в (1), (2) и (3) не уточняется вид функции вейвлета. В этом состоит отличие вейвлет-анализа от анализа Фурье. Вейвлет-анализ строится не на определенном виде функций-вейвлетов, а на определенных свойтвах этих функций.
Самыми важными свойствами вейвлета являются допустимость и регулярность. Квадратно-интегрируемая функция
 (t),
удовлетворяющая условию допустимости,
(t),
удовлетворяющая условию допустимости,
может быть использована для анализа, а затем для восстановления сигнала без потери информации.В (4)
 (
(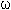 ) означает преобразование Фурье функции
) означает преобразование Фурье функции  (t
). Условие допустимости подразумевает, что преобразование Фурье функции
(t
). Условие допустимости подразумевает, что преобразование Фурье функции  (t) становится
равным нулю на нулевой частоте, т.е.
(t) становится
равным нулю на нулевой частоте, т.е.
Это значит, что вейвлеты должны иметь полосу частот как спектр. Нулевое значение на нулевой частоте также значит, что среднее значение вейвлета на всей временной оси должно быть равно нулю (в отличие от среднего значения гармоник Фурье-анализа). Из этого утверждения легко зделать вывод, что по виду вейвлет-функции представляют собой волны.
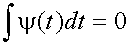 (6)
(6)
Из (1) вытекает, что частотно-временной результат вейвлет-преобразования равен квадрату входного сигнала, что для большенства приложений нежелательно. Для этого на вейвлет накладывают еще некоторые ограничения, чтобы результат вейвлет-преобразования убывал вместе с уменьшением масштаба s. Эти ограничения называют ограничениями регулярности, которые состоят в том, чтобы вейвлет-функция была гладкой и концентрировалась как во временной, так и в частотной области. Условие регулярности можно объяснить, используя понятие исчезающих моментов.
.Если вейвлет-преобразование (1) представить как разложение в ряд Тейлора при t = 0 до порядка n (
 = 0 для простоты), мы
получим:
= 0 для простоты), мы
получим:
Здесь f (p) - производная порядка p функции f и O(n+1) представляет собой остаток разложения.
Обозначив моменты вейвлета как Mp,
можно переписать (7) как конечную сумму
Из условия допустимости следует равенство 0 момента M0 = 0, т.е. первое слагаемое в правой части (9) равно 0. Если теперь нам удастся зделать нулевыми остальные моменты до Mn, коэффициенты вейвлет-преобразования
 (s,
(s, )
будут убывать также быстро как sn+2 в случае
гладкого сигнала f(t). Это называют исчезающими
моментами. Если у вейвлета N исчезающих моментов, то порядок
приближения вейвлет-преобразования равен N. Моменты необязательно
должны быть равны 0, очень маленькое значение часто считают достаточным.
)
будут убывать также быстро как sn+2 в случае
гладкого сигнала f(t). Это называют исчезающими
моментами. Если у вейвлета N исчезающих моментов, то порядок
приближения вейвлет-преобразования равен N. Моменты необязательно
должны быть равны 0, очень маленькое значение часто считают достаточным.
Таким образом, условие допустимости дает нам волну, регулярность и исчезающие моменты дают нам быстрое убывание, и вместе эти 2 условия дают нам вейвлет.
Зная, что такое вейвлет-преобразование, необходимо сделать его теперь применимым на практике. Однако, есть 3 свойства преобразования, которые делают сложным его применение в виде (1).
Первое - избыточность непрерывного вейвлет-преобразования (НВП).
Второе - бесконечное количество вейвлетов (масштаб можно изменять бесконечно).
Третье - для большинства функций вейвлет-преобразование не может быть вычислено аналитически, только при помощи численных методов и аналоговых компьютеров.
Так возникает необходимость решить эти 3 проблемы и создать быстрый алгоритм вычисления вейвлет-преобразования.
Избавимся от избыточности:
НВП преобразует одномерный сигнал в двумерное представление по частоте и по времени, которое является избыточным. Для решения проблемы избыточности вводят понятие дискретных вейвлетов. Дискретные вейвлеты не могут быть масштабированы и сдвигаемы по временной оси непрерывно. Эти две операции над дискретными вейвлетами можно проводить только дискретными шагами. Это достигается преобразованием вейвлет-функции (3) к следующему виду
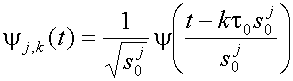 (10)
(10)
Хотя это называется дискретным вейвлетом, оюычно это представляет собой
(кусочно) непрерывную функцию. В
(10) j и k - целые числа, а s0
> 1 - шаг расширения. Коэффициент сдвига  0
зависит от шага расширения. Эффект дискретизации вейвлета заключается в том,
что теперь выборка в частотно-временной области осуществляется дискретными
интервалами. Обычно принимают s0 = 2. Коэффициент
сдвига принимают
0
зависит от шага расширения. Эффект дискретизации вейвлета заключается в том,
что теперь выборка в частотно-временной области осуществляется дискретными
интервалами. Обычно принимают s0 = 2. Коэффициент
сдвига принимают  0 =
1.
0 =
1.

Рис. 1
Локализация дискретных вейвлетов в мсштабно-временном пространстве.
Когда для преобразования непрерывного сигнала используют дискретные вейвлеты, результат представляет собой ряд вейвлет-коэффициентов и называется разложением в вейвлет-ряд. При этом обязательным является условие восстановления сигнала по коэффициентам разложения. достаточным для восстановления сигнала является ограничение (11) для энергии вейвлет-коэффициентов.
| f ||2 -энергия f(t), A > 0, B <
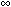 ;
A, B не зависят от f(t). Когда
(11)
выполняется, семействр базовых функций
;
A, B не зависят от f(t). Когда
(11)
выполняется, семействр базовых функций  j,k(t
) где j, k Z называют
фреймом с границами A и B. Если A = B фрейм
называют узким и дискретные вейвлеты представляют собой ортонормальный
базис.Если A
j,k(t
) где j, k Z называют
фреймом с границами A и B. Если A = B фрейм
называют узким и дискретные вейвлеты представляют собой ортонормальный
базис.Если A 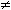 B, точное
восстановление сигнала возможно с условием использования двойного фрейма, в
котором вейвлет, используемый при разложении отличается от вейвлета,
используемого при восстановлении сигнала.
B, точное
восстановление сигнала возможно с условием использования двойного фрейма, в
котором вейвлет, используемый при разложении отличается от вейвлета,
используемого при восстановлении сигнала.
Вернемся от фреймов к удалению избыточности. Приведем дискретные вейвлеты к ортонормальному базису. Дискретные вейвлеты могут быть ортогональны своим собственным расширениям и сдвигам благодаря специальному выбору материнского вейвлета, что значит:
Начальный сигнал может быть восстановлен суммированием ортогональных базисных вейвлет-функций, умноженных на коэффициенты вейвлет-преобразования.
(13) - обратное дискретное вейвлет-преобразование.
Ортогональность все же не является непременным условием вейвлет-преобразования сигналов. В некоторых приложениях выбор неортогональных вейвлетов (избыточное преобразование) помогает уменьшить чувствительность к шумам и улучшить нечувствительность к сдвигу сигнала. Одним из недостатков дискретного вейвлет-преобразования является его чувствительность к сдвигу во времени исходного сигнала. Вейвлет преобразования сигнала и его версии, сдвинутой во времени не будут явялятся копиями друг-друга, только сдвинутыми по времени.
Попытаемся уменьшить количество вейвлетов, необходимых для преобразования сигнала.
Количество сдвигов вейвлетов ограничено длительностью сигнала, т.е. мы имеем границу по времени. Попытаемся найти границу по количеству шагов масштабирования.
Из (5) видно, что вейвлет имеет полосу частот как спектр. Из преобразования Фурье следует, что сжатие по времени равновильно растягиванию спектра и сдвигу его в сторону верхних частот.
Это значит, что сжатие вейвлета по времени в 2 раза растянет его спектр частот в 2 раза и также сдвинет все частотные составляющие спектра вверх. Используя эти выводы, мы может перекрыть конечный спектр нашего сигнала спектрами расширяемых вейвлетов также, как во временной области мы перекрываем весь наш сигнал за счет перемещения вейвлетов "вдоль" него во времени. Для хорошего качества представления спектра сигнала, перекрывающие его спектры вейвлетов должны касаться друг друга, как будто они стоят, держась за руки (рис. 2). Этого можно достичь при правильном построении вейвлетов.

Рис. 2
Касающиеся спектры вейвлетов, полученные в результате масштабирования материнского вейвлета во временной области.
Таким образом, вейвлет можно представить, как частотный фильтр. Тогда ряд вейвлетов можно назвать банком фильтров. Если мы обратим внимание на отношение центральной частоты спектра вейвлета к ширине этого спектра, то увидим, что это отношение постоянно для всех вейвлетов. Обычно это отношение называют фактором верности Q фильтра, и в случае вейвлетов говорят о постоянном Q банке фильтров.
Из вышесказанного следует, что исследуемый сигнал должен иметь конечную энергию. Если сигнал будет иметь бесконечную энергию, будет невозможно перекрыть частотный спектр сигнала и его временную доительность длительностями и спектрами вейвлетов. Математически это представляет собой следующее:
Возникает вопрос, как перекрыть весь спектр сигнала до самого нуля. Каждый раз при растяжении вейвлет во временной области в 2 раза, его полоса частот сжимается в 2 раза. Другими словами, с каждым растяжением вейвлета мы перекрываем только половину остающегося спектра, что означает, что для перекрытия всего спектра сигнала нам будет необходимо бесконечное число вейвлетов.
Решением этой проблемы является использование некоторой "пробки" для перекрытия дыры в остающемся спектре, когда она достаточна мала. Этой "пробкой" является так называемая масштабирующая функция, которая представляет собой фильтр низких частот. Масштабирующую функцию также иногда называют усредняющим фильтром.
Масштабирующую функцию как функцию с узкой полосой частот тоже можно представить как вейвлет разложение в виде (13):
Так как мы выбрали масштабирующую функцию
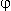 (t
) таким образом, что ее спектр успешно перекрывает остаток спектра сигнала,
выражение
(16) использует бесконечное количество вейвлетов до некоторого масштаба
j (см. рис.
3). Это значит, что если при разложении сигнала мы используем
масштабирующую функцию и ряд вейвлетов, масштабирующая функция перекрывает
своим спектром ту часть сигнала, которая иначе была бы перекрыта всеми
вейвлетами до масштаба j. Остаток же спектра сигнала, неперекрытый спектром
масштабирующей функции, перекрывается вейвлетами. Так, мы ограничили количество
вейвлетов в разложении и сделали его конечным.
(t
) таким образом, что ее спектр успешно перекрывает остаток спектра сигнала,
выражение
(16) использует бесконечное количество вейвлетов до некоторого масштаба
j (см. рис.
3). Это значит, что если при разложении сигнала мы используем
масштабирующую функцию и ряд вейвлетов, масштабирующая функция перекрывает
своим спектром ту часть сигнала, которая иначе была бы перекрыта всеми
вейвлетами до масштаба j. Остаток же спектра сигнала, неперекрытый спектром
масштабирующей функции, перекрывается вейвлетами. Так, мы ограничили количество
вейвлетов в разложении и сделали его конечным.
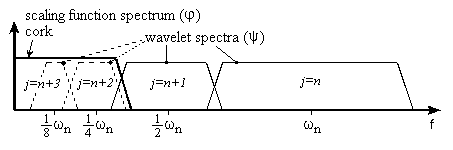
Рис. 3
Замена бесконечного набора вейвлетов одной масштабирующей функцией.
Безусловно, при использовании масштабирующей функции мы теряем часть информации. Сигнал может быть восстановлен без потерь, но некоторые особенности сигнала, которые можно было бы выявить при масштабном изменении вейвлетов, останутся невыясненными. Таким образом, становится важность выбора ширины спектра масштабирующей функции. Чем он шире, тем больше детальной информации остается невыясненной.
Низкочастотный спектр масштабирующей функции позволяет нам сформулировать некоторое условие допустимости сродни (6)
котрое показывает, что нулевой момент масштабирующей функции не может исчезнуть.
Подводя итог, еще раз следует упомянуть, что если один вейвлет можно считать частотным филтром, а масштабирующую функцию можно считать низкочастотным фильтром, то ряд отмасштабированных вейвлетов вместе с масштабирующей функцией представляет собой банк филтров.
Две из проблем, упомянутых в пункте 4, решены. Попытаемся выяснить тонкости вычислениявейвлет-преобразования.
Если представлять вейвлет-преобразование как банк фильтров, можно считать, что преобразование сигнала вейвлетом представляет собой прохождение сигнала через определенный частотный фильтр и выходы определенных ступеней фильтрации должны представлять собой вейвлет коэффициенты и коэффициенты преобразования масштабирующей функции. Эта идея анализа сигнала путем его пропускания через ряд фильтров получила название субполосного кодирования.

Рис. 4
Разделение спектра сигнала посредством итерированного банка фильтров.
Есть два подхода к осуществлению субполосного кодирования. Первый - рассчитать множество частотных фильтров и пропустить через них исходный сигнал. Это сложный подход, но удобен тем, что ширина полосы частот, пропускаемой отдельным фильтром, может быть выбрана свободно и, таким образом, мы можем заострять свое внимание на определенных частях спектра исследуемого сигнала. Но этот подход является очень сложным. Другой подход заключается в том, чтобы разделить исходный спектр сигнала на 2 части - высокочастотную и низкочастотную. Высокочастотная часть содержит мельчайшие детали, которые нас интересуют. Однако низкочастотная часть также может содержать информацию о деталях исходного сигнала, поэтому мы можем снова разделить ее на 2 части и т.д., пока мы не будем удовлетворены количеством частотных полос. Таким образом второй подход состоит в создании итерированного банка фильтров. Обычно количество полос в результате работы банка фильтров ограничивается объемом исходной информации или возможностями вычислительной техники. Процесс деления сигнала показан на рисунке 4. Преимущество этой схемы состоит в том, что нам необходимо создать только 2 фильтра, недостаток - в том, что покрытие спектра сигнала ограничено.
Во многих практических приложениях используется выборка исходного сигнала. Для анализа дискретных сигналов постараемся привести вейвлет-преобразование к дискретной форме. Следует помнить, что дискретные вейвлеты не являются дискретными во времени, дискретными являются только шаг масштабирования и сдвига во времени. Реализация вейвлет банка фильтров в качестве банка цифровых фильтров кажется хорошим решением. Но всякое решение требует проверки.
Из (16) следует, что масштабирующая функция может быть представлена как комбинация вейвлетов от минус бесконечности до некоторого масштаба j. Если к спектру масштабирующей функции добавить спектр вейвлета, нами будет получена новая масштабирующая функция со спектром вдвое шире, чем у предыдущей. Смысл этого объединения состоит в том, что первую масштабирующую функцию можно выразить через вторую, так как вся информация для первой масштабирующей функции содержится во второй. Это можно формально выразить через двумасштабное представление.
 (18)
(18)
Из этого представления следует, что масштабирующая функция на некотором масштабе может быть выражена через сдвинутую масштабирующую функцию на следующем более мелком масштабе, (здесь более мелкий масштаб означает ьольше деталей).
Первая масштабирующая функция заменила ряд вейвлетов. Таким образом, мы можем также выразить вейвлеты этого ряда через сдвинутые масштабирующие функции следующего масштаба. Для вейвлета масштаба j можно записать:
что представляет собой двумасштабное отношение вейвлета и масштабирующей функции более мелкого масштаба.
Так как наш сигнал можно выразить через расширенные и сдвинутые вейвлет до масштаба j-1, его также можно выразить через масштабированные и сдвинутые масштабирующие функции масштаба j.
Если в этом выражении мы поднимемся до масштаба j-1, нам необходимо будет добавить вейвлеты, чтобы сохранить тот же уровень детализации:
Если масштабирующая функция
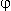 j,k(t
) и вейвлеты
j,k(t
) и вейвлеты  j,k(t) ортонормальны
или представляют собой узкий фрейм, коэффициенты
j,k(t) ортонормальны
или представляют собой узкий фрейм, коэффициенты  j-1(k
) и
j-1(k
) и  j-1(k)
можно найти как:
j-1(k)
можно найти как:
Если теперь мы заменим
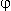 j,k(t
) и
j,k(t
) и  j,k(t)
в выражениях соответственно отмасштабированными и сдвинутыми версиями
(18) и
(19) и проведем некоторые преобразования, мы увидим следующий
результат:
j,k(t)
в выражениях соответственно отмасштабированными и сдвинутыми версиями
(18) и
(19) и проведем некоторые преобразования, мы увидим следующий
результат:
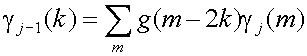 (24)
(24)
 (k)
на самом крупном масштабе.
(k)
на самом крупном масштабе.
Из теории обработки сигналов известно, что суммы как (23) и (24) являются тем же, что и цифровой фильтр. Так как мы знаем, что коэффициенты
 j(k
) поступают от низкочастотной части разделенного спектра сигнала,
коэффициенты h(k) в
(23) должно быть формируют низкочастотный фильтр. А так как мы
знаем, что коэффициенты
j(k
) поступают от низкочастотной части разделенного спектра сигнала,
коэффициенты h(k) в
(23) должно быть формируют низкочастотный фильтр. А так как мы
знаем, что коэффициенты  j(k
) являются результатом высокочастотной части разделенного спектра сигнала,
коэффициенты g(k) в
(24) должны формировать высокочастотный фильтр. Значит
(23) и
(24) вместе формируют одну ступень итерированного банка фильтров
и коэффициенты h(k) можно называть масштабирующим фильтром, а g(k)
- вейвлет-фильтром.
j(k
) являются результатом высокочастотной части разделенного спектра сигнала,
коэффициенты g(k) в
(24) должны формировать высокочастотный фильтр. Значит
(23) и
(24) вместе формируют одну ступень итерированного банка фильтров
и коэффициенты h(k) можно называть масштабирующим фильтром, а g(k)
- вейвлет-фильтром.
Пришло время решить последнюю проблему - выбор спектра масштабирующей функции. Так как на каждой итерации банка фильтров объем выборки для следующего шага уменьшается в два раза, в конце концов остается только один отсчет ( в крайнем случае). На этом последнем шаге становится ясно, что это последняя итерация и таким образом, ширина спектра нашей масштабирующнй функции ограничивается автоматически. Обычно все же процесс итерирования останавливают, когда объем выборки становится меньше длины масштабирующего или вейвлет-фильтра, в зависимости от того, который из них длинее. Таким образом, длина наибольшего из фильтров определяет ширину спектра масштабирующей функции.
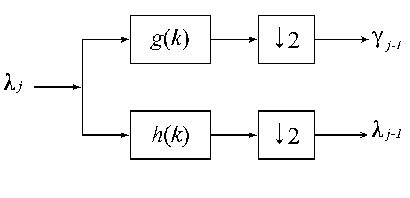
Рис. 5
Реализация (23) и (24) как одной ступени итерированного банка фильтров.
Вейвлет-преобразование преобрело практически реализуемую форму в результате его аппроксимации банком фильтров.


Рис. 6
Некоторые масштабирующие функции (наверху) и вейвлеты(внизу)
- Burrus, C. S. and R. A. Gopinath, H. Guo.
INTRODUCTION TO WAVELETS AND WAVELET TRANSFORMS, A PRIMER. Upper Saddle River, NJ (USA): Prentice Hall, 1998.
- Calderbank, A. R. and I. Daubechies, W. Sweldens, B.-L. Yeo
WAVELET TRANSFORMS THAT MAP INTEGERS TO INTEGERS.
Proceedings of the IEEE Conference on Image Processing. Preprint, 1996.
IEEE Press, 1997. To appear.
-
Daubechies, I.
TEN LECTURES ON WAVELETS. 2nd ed.
Philadelphia: SIAM, 1992.
CBMS-NSF regional conference series in applied mathematics 61.
- Hubbard, B. Burke
THE WORLD ACCORDING TO WAVELETS.
Wellesey, MA (USA): A K Peters, 1996.
- Kaiser, G. A FRIENDLY GUIDE TO WAVELETS.
Boston: Birkhдuser, 1994.
- Körner, T. W.
FOURIER ANALYSIS.
Cambridge, UK: Cambridge University Press, 1996.
- Mallat, S. G.
A THEORY FOR MULTIRESOLUTION SIGNAL DECOMPOSITION: THE WAVELET REPRESENTATION.
IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 11, No. 7
(1989), p. 674- 693.
- Sheng, Y.
WAVELET TRANSFORM.
In: The transforms and applications handbook. Ed. by A. D. Poularikas. P.
747-827.
Boca Raton, Fl (USA): CRC Press, 1996.
The Electrical Engineering Handbook Series.
- Vetterli M. and C. Herley.
WAVELETS AND FILTER BANKS: THEORY AND DESIGN.
IEEE Transactions on Signal Processing, Vol. 40, No. 9 (1992), p. 2207-2232.
- Weiss, L. G.
WAVELETS AND WIDEBAND CORRELATION PROCESSING.
IEEE Signal Processing Magazine, January (1994), p. 13-32.
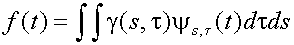 (2)
(2)
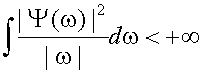 (4)
(4)
 (5)
(5)
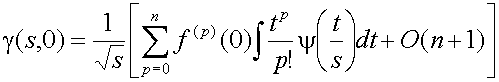 (7)
(7)
 (8)
(8)
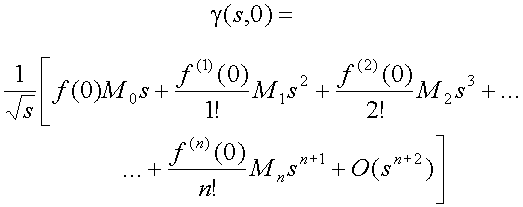 (9)
(9)
 (11)
(11)
 (12)
(12)
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
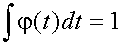 (17)
(17)
 (19)
(19)
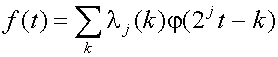 (20)
(20)
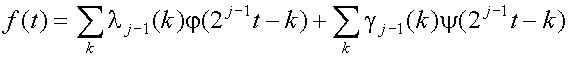 (21)
(21)
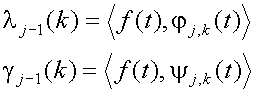 (22)
(22)
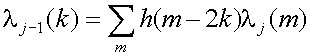 (23)
(23)