В.Н. Копенков. Эффективные алгоритмы локального дискретного вейвлет-преобразования с базисом Хаара


В работе предлагаются два новых быстрых алгоритма вычисления локального дискретного вейвлет-преобразования одномерного сигнала на примере вейвлет-базиса Хаара, приводятся выражения для их вычислительной сложности, производится их сравнение друг с другом и с известным алгоритмом быстрого вейвлет-преобразования. Приведены рекомендации по использованию каждого из предложенных алгоритмов. В частности, указаны области «предпочтения» этих алгоритмов, то есть параметры задачи вычисления вейвлетпреобразования, для которых эти алгоритмы вычислительно эффективны. На основе анализа сложности алгоритмов, а также с учетом дополнительных возможностей, которые дает рекурсивный алгоритм, делается вывод о его преимуществе по сравнению с альтернативным и с известным алгоритмом быстрого вейвлет-преобразования. Представлено обобщение рассмотренных алгоритмов на 2-х мерный случай Ссылка: "KO321317.pdf"[pdf, 614 Kb]



Введение

Вейвлет-анализ является в настоящее время одним из наиболее эффективных инструментов, предназначенных для исследования локальных пространственных и частотных характеристик сигналов [1,2]. В настоящей работе для решения задач локального вейвлет-анализа данных предполагается заменить известную иерархическую вычислительную конструкцию, присущую хорошо известным алгоритмам расчета дискретного вейвлет-преобразования (ДВП), таким как «algorithme a trous» [3] и быстрый алгоритм дискретного ортогонального вейвлет-разложения С.Малла [2] (БВП). Замена конструкции предполагает ее трансформацию от иерар- хической схемы вычислений, используемой в известных алгоритмах, к схеме, в которой вычисление коэффициентов для вейвлетов каждого уровня производится последовательно для всех его позиций на цифровом сигнале в рекурсивном режиме [4-6].

Данное изменение вычислительной конструкции вейвлет-преобразования позволяет отойти от «блочного» характера вычислений [1,2], который обычно приводит либо к избыточной в вычислительном плане схемы последовательного вычисления вейвлет-преобразования (для сильно перекрывающихся блоков анализа), либо к снижению качественных показателей анализа (при расположении блоков вейвлет-преобразования без перекрытий). Изменение вычислительной конструкции в параллельную или параллельно-рекурсивную форму, которая хорошо приспособлена к задаче локального «скользя- щего» анализа цифровых сигналов и изображений [4-6], приводит, в частности, к существенному снижению сложности обработки. Работа организована следующим образом.

В первом разделе приводится определение вейвлетов, дискретного вейвлет-преобразования одно- мерного сигнала, дается вид вейвлет-базисов Хаара. Этот раздел является вводным и содержит только известные сведения из теории вейвлетов, доступные, например, в монографиях [1,2]. Во втором разделе приводится описание прямого и быстрого алгоритма вычисления дискретного вейвлет-преобразования, приводятся выражения для его вычислительной сложности.

В третьем разделе дается определение локального дискретного вейвлет-преобразования одномерного сигнала, приводится выражения для сложности реализации локального вейвлет-преобразования в случае, применения известных алгоритмов, описанных во втором разделе. Этот раздел содержит очевидное развитие известных результатов.




1. Вейвлет-преобразование (ВП) и базис Хаара

 1.1 Непрерывный случай

Функция psi(t) называется вейвлетом (всплеском), если для нее выполняются следующие условия [1,2]:

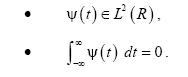
Функцию двух переменных a,b, задаваемую выражением
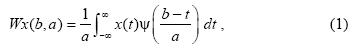
называют вейвлет-преобразованием вещественной функции x(t) [1,2]. Вейвлеты вида {2m/2psi(2mt-k)} для фиксированного m являются базисом подпространства Wm = Vm\Vm-1, где m - целое, в ортогональном кратномасштабном анализе (ОКА), который определен следующим образом [1,2].
Определение. Система подпространств Vm в пространстве L2(R) называется ОКА, если она удовлетворят условиям:

Одним из наиболее известных вейвлет-базисов является базис Хаара [1,2], скейлинг-функция которого определяется следующим образом:
Вейвлеты Хаара имеют вид:

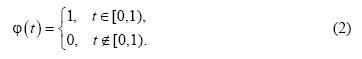
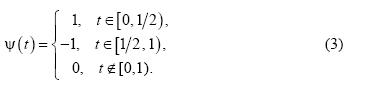
1.2 Дискретный случай

Отсчеты дискретного сигнала x(n) интерпретируются как коэффициенты разложения этого сигнала по скейлинг-функциям (2). Таким образом, дискретный сигнал x(n) представляется как кусочно-постоянная функция и, следовательно, интерпретируются как функция пространства V0. Для сигнала x(n) (n>=0) с нулевым средним дискретное вейвлет-преобразование задается выражением:

Для сигналов со средним, отличным от нулевого, для обратимости преобразования (4) добавляется значение скалярного преобразования со скейлинг-функцией максимального масштаба (берется из размеров сигнала).


2. Алгоритм быстрого вейвлет-преобразования

Расчет коэффициентов вейвлет-преобразования непосредственно по выражению (4) является достаточно трудоемкой процедурой. Действительно, в ортогональном (безизбыточном) представлении (4) дискретного сигнала длины N = 2L участвуют N-1 вейвлетов различных масштабов m = 1..L и одна скейлинг-функция размера N. Каждый вейвлет масштаба m имеет размер S(m) = 2m (число ненулевых отсчетов), число вейвлетов этого масштаба – K(m)=N/2m=2L-m Поэтому для расчета коэффициентов ортогонального вейвлет-преобразования (4), то есть соответствующих скалярных произведений для всех вейвлетов и скейлинг-функции, требуется, очевидно

операций сложения (нормирующие множители здесь и далее не учитываем, умножение на единицу также игнорируется). Идея ускорения расчета преобразования (4) заключается в простом использовании того факта, что пространства Vm есть прямая сумма пространств Wm и Vm-1 Тогда, имея текущее представление функции в пространстве Vm, мы можем получить с помощью проекций представления в пространствах Vm-1 и Wm-1[1-3]. Соответствующий быстрый алгоритм ДВП имеет вид [1-3]:

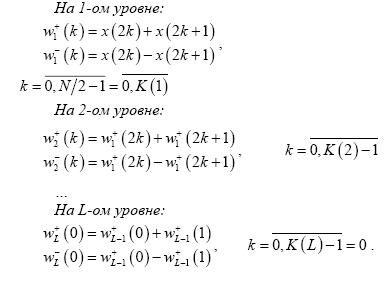
Эту расчетную процедуру иногда называют быстрым вейвлет-преобразованием (БВП), а иногда – алгоритмом Малла, по имени человека, доказавшего теорему, которая показывает корректность именно такой процедуры расчета [2]. Вычислительная сложность такого алгоритма, очевидно, составляет [1-3]

U1(N)=2(N-1) (5) операций сложения, необходимых для вычисления всех коэффициентов дискретного ортогонального ВП. В дальнейшем мы будем пользоваться выражением для приведенной вычислительной сложности, то есть числу операций, приходящихся на один отсчет исходного сигнала. В этом случае, получаем следующее выражение для вычислительной сложности:

U1*(N)=U1(N)/N=2(N-1)/N=2 (6)


3. Локальное ДВП цифрового сигнала

На практике часто приходится использовать не полное разложение сигнала, а его локальное разложение. При локальном разложении каждый возможный фрагмент сигнала длины M2 =2L2 должен быть подвергнут разложению по заданной системе функций. Такую обработку обычно называют обработкой в скользящем окне [4-6], поскольку область обработка из M2 отсчетов последовательно сдвигается, занимая все возможные положения на оси дискретного аргумента. Обработка в скользящем окне является неотъемлемой частью целого ряда прикладных задач, таких как обнаружение и распознавание локальных объектов/сигналов, локальный анализ, адаптивные преобразования и других [4,5].

При использовании для расчета коэффициентов локального вейвлет-преобразования алгоритма БВП, описанного во втором разделе настоящей работы, сложность обработки в пересчете на число областей/фрагментов анализа составляет, очевидно

U*2(M2)=(N-M2+1)U1(M2)/(N-M2+1)=(2M2-1) (7)
операций сложения.

Следует отметить, что в большинстве практических задач локального анализа сигналов и изображений нет необходимости получать все возможные коэффициенты разложения [4,5]. Обычно диапазон интересующих функций разложения уже, обычно он ограничен (по частоте) снизу и сверху. Снизу – максимальными размерами объектов, сверху – их минимальными размерами и размерами их существенных деталей. Поэтому введем в рассмотрение размер M1, который ограничивает минимальный уровень вейвлетов в разложении (4). Тогда вычислительная сложность БВП для диапазона уровней [L1,L2] составит:

U*2(L1,L2)=2(2L2-1) (8)
операций сложения и не зависит от положения «нижнего» уровня L1.


Литература

  1. I. Daubechies Ten Lectures on Wavelets // CBMS-NSF Lecture Notes nr. 61, SIAM, 1992. – 377 p.
  2. S. Mallat A wavelet tour of signal processing // Aca- demic Press, 1999 – 637 p.
  3. M. Holschneider, A real-time algorithm for signal analy- sis with help of the wavelet transform // M. Holschneider, R. Kronland-Martinet, J. Morlet, Ph. Tchamitchian Wave- lets, Time-Frequency Methods and Phase Space, Chapter A. Berlin: Springer-Verlag, 1989. - pp. 289-297.
  4. A.V. Chernov Fast Method for Local Image Processing and Analysis // A.V. Chernov, V.V. Myasnikov, V.V. Sergeyev Pattern Recognition and Image Analysis, Vol.9, No.4, 1999, pp. 572-577.
  5. V.V. Myasnikov Methods for Designing Recursive FIR Filters // Proceedings of International Confer- ence “Computer Vision and Graphics” (ICCVG 2004), Warsaw, Poland, September 22-24, 2004, Springer, pp.845-850.
  6. Копенков В.Н., Быстрые алгоритмы локального дис- кретного вейвлет-преобразования с базисом Хаара // Копенков В.Н., Мясников В.В НТК с межд. участием: «ПИТ-2006» Том 2. 2006 г. Самара. стр. 113-118.