Л. Левкович-Маслюк, А. Переберин. Лифтинг-схема, мультивейвлеты
Лекция содержит краткую, вводную информацию о лифтинг-схеме (вейвлет-преобразовании второго поколения) и мультивейвлетах (векторнозначном расширении вейвлетов). Ссылка: http://algolist.manual.ru/compress/image/leo_lev/lecture4/wav4_1.php
Целочисленное вейвлет-преобразование
Напомним условия точного восстановления для двух пар биортогональных фильтров. Рассмотрим две пары фильтров: (h, g) и
 . Мы хотим проводить разложение при помощи свертки с
. Мы хотим проводить разложение при помощи свертки с 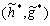 , а восстановление – при помощи (h,g).
В терминах z-преобразования разложение на высокие и низкие частоты с прореживанием вдвое имеет вид:
, а восстановление – при помощи (h,g).
В терминах z-преобразования разложение на высокие и низкие частоты с прореживанием вдвое имеет вид:

Записав в аналогичном виде процесс восстановления с помощью пары (h, g), и приравняв результат к X(z), получаем :
Метод лифтинга (lifting) позволяет:
Строить новые фильтры, удовлетворяющие (1), из уже имеющихся.
Выполнять вейвлет-преобразование быстрее за счет декомпозиции на элементарные шаги лифтинга (lifting steps).
Шаги лифтинга используют разбиение сигнала на две компоненты – с четными и нечетными индексами. Поэтому эта методика естественно формулируется в терминах полифазных матриц (polyphase matrix). Сначала введем матрицу модуляции (modulation matrix):
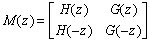 (2)
(2)
Аналогично определяется M(z). Условие (1) эквивалентно тому, что
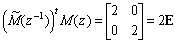 (1')
(1')
Мы предполагаем, что все фильтры содержат конечное число ненулевых коэффициентов, т.е. выражения типа H(z) являются многочленами Лорана (могут содержать и положительные и отрицательные степени z); для краткости будем называть их просто многочленами. Введем четную и нечетную части наших многочленов :
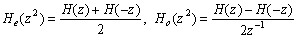
Тогда
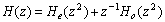
Полифазная матрица имеет вид:

Она связана с матрицей модуляции так:
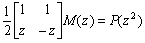
Подставив это выражение в (1’), получим условие точного восстановления в такой форме:
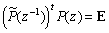 (3)
(3)
Если предположить, что определитель полифазной матрицы равен 1 (этого всегда можно достичь умножением на подходящий одночлен G(z)), то из (3) получаем обычное выражение, связывающее основные и дуальные фильтры:
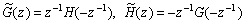
Полифазная матрица позволяет записать вейвлет-преобразование через действие компонент фильтров на компонентах сигнала. Например, этап разложения выглядит так:
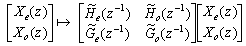
/ Предположим, что имеется пара фильтров H(z), G(z) такая, что det(P(z))=1. Такая пара называется комплементарной (complementary). Оказывается, легко описать все конечные фильтры G1(z), образующие комплементарную пару с фиксированным фильтром H(z). А именно, пара H(z), G1(z) комплементарна тогда и только тогда, когда:

/ где S – произвольный многочлен. Это преобразование пары фильтров называется лифтингом. Оно эквивалентно преобразованию полифазной матрицы

/ При помощи алгоритма Евклида вычисления наибольшего общего делителя многочленов можно получить следующее разложение полифазных матриц (основной и дуальной):
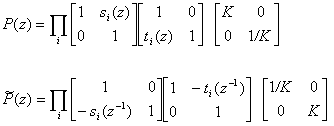 (4)
(4)
/ Обратим внимание на то, что масштабирование, заданное в (4) матрицей также можно представить в виде шагов лифтинга, причем не единственным образом. Разложение (4) – “анатомия” одного шага вейвлет-преобразования. Любое биортогональное ВП можно представить в таком виде. Непосредственный результат – сокращение числа операций (до 50%). Но главное значение лифтинга не в этом. Если перейти от z-преобразования к записи в компонентах самого сигнала, то полученные формулы удобно модифицировать для локальной адаптации к сигналу, а также к краевым условиям. Этот подход очень близок к тому, который использовался при построении адаптивных многосеточных разностных схем в вычислительной физике. Идея лифтинга близка к идее пирамиды лапласианов. Однако первоначально лифтинг возник в рамках идеологии предсказания-уточнения (predict-update). Применение лифтинговых матриц-сомножителей к сигналу эквивалентно следующей процедуре. Исходный сигнал разбивается на 2 компоненты (например, четную и нечетную). Нечетные элементы “предсказываются” по значениям четных, находится разность (ошибка предсказания), а затем по этой ошибке корректируется четная часть (например, чтобы сохранить неизменным среднее значение). Например, можно предсказывать нечетные компоненты сигнала по четным при помощи кубической интерполяции. Запишем шаги схему лифтинга в терминах компонентов векторов:
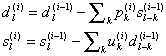
Шаги прямого преобразования:

Шаги обратного преобразования:

Как было отмечено выше, лифтинг позволяет не только анализировать имеющиеся фильтры, но и строить новые, то есть конструировать новые схемы вейвлет-преобразований, в том числе и такие, которые другим способом получить либо очень трудно, либо невозможно (в частности, преобразования, базисные функции которых не являются сдвигами и сжатиями одной функции). Идеология "предсказание-уточнение" является в этом смысле чем-то вроде итерационного метода пострения фильтров: взяв в качестве начального приближения набор "плохих" фильтров, можно, последовательно применяя к этим фильтрам шаги лифтинга, получать новые фильтры с определенными свойствами. При этом, если исходные фильтры удовлетворяют (1), то на каждом шаге лифтинга условие (1) не будет нарушаться , то есть любое построенное таким образом преобразование заведемо гарантирует точное восстановление.
В качестве начального приближения обычно берутся фильтры, выделяющие соответственно четные и нечетные компоненты исходного сигнала. В терминах вейвлетов это означает, что вейвет-базисом становится просто подмножество скейлинг-функций. Такие вейвлеты называются ленивыми (lazy wavelet), они практически неприменимы для сколь-либо удовлетворительной обработки сигналов, зато активно используются в качестве "заготовки" для построения констукций различной сложности.
Лифтинговая запись имеет еще одно полезное свойство: если компоненты сигнала – целые числа, то можно сделать целыми и все промежуточные результаты шагов лифтинга. При этом обращение остается точным, т.к. представляет собой те же самые шаги, выполненные в обратном порядке. Тем самым любое ВП можно заставить переводить целые числа в целые. Шаг целочисленного (integer-to-integer) ВП записывается с помощью лифтинга так:
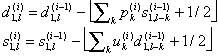 (6)
(6)
Оказывается, что целочисленное ВП можно использовать при сжатии изображений без потерь, хотя имеются только предварительные результаты, указывающие на то, что после целочисленного ВП применение обычных методов символьного кодирования становится более эффективным.
Имеется и нелинейная версия предсказания-уточнения. Дело в том, что при работе в окрестности резких перепадов любые фильтры, полученные из интерполяционных соображений, дают плохой результат и при предсказании, и при уточнении. Нелинейность возникает в тех методах, где сигнал предварительно тестируется на локальные скачки, и предсказание делается по участкам, не содержащим скачков. Такого рода адаптация к сигналу хорошо известна в вычислительной физике, и в применении к многомасштабному разложению сигналов была впервые, по-видимому, реализована А.Хартеном в рамках его общей теории многомасштабного представления (см. [1]).
Мультивейвлеты
Мультивейвлеты (multiwavelets) – это векторнозначное обобщение вейвлетов. Они предназначены для разложения “многоканальных” сигналов, имеющих не одну, а несколько компонент. Впрочем, к такому виду можно привести и скалярный сигнал (переходом к четным и нечетным компонентам, например). Мультивейвлеты определяются точно такими же (внешне!) уравнениями рескейлинга, что и обычные вейвлеты.
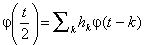
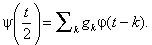
Их привлекательность том, что они:
Как и обычные вейвлеты, порождают МА.
Сильнее локализованы в пространстве, что может оказаться удобно в ряде задач (например, в матфизике).
Допускают быстрый алгоритм преобразования (алгоритм Малла с матричными коэффициентами дословно переносится на этот случай)
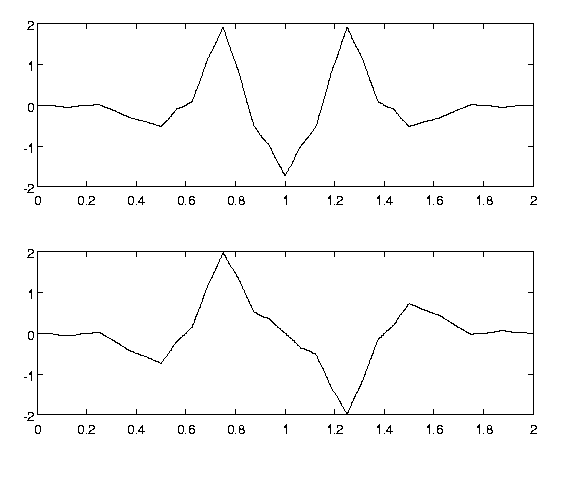
Однако построить мультивейвлеты оказалось сложнее, чем обычные вейвлеты. Дело в том, что уравнения скейлинга имеют матричные коэффициенты, которые не коммутируют между собой. Поэтому найти подходящий набор коэффициентов, дающий гладкие решения уравнения рескейлинга, довольно сложно. Первый пример ортогональных и непрерывных мультивейвлетов получен Джеронимо, Хардином и Массопустом (Geronimo, Hardin, Massopust – GHM). Скейлинг-функции и вейвлеты в их примере были кусочно-самоподобными, и пример был построен с использованием методов из теории ИФС (итерационных функциональных систем), порождающих, вообще говоря, фрактальные функции. GHM-мультивейвлеты и скейлинг-функции показаны на рисунках 1 и 2:
 (6)
(6)
Рисунок 1- Скейлинг–функции GHM.
 (6)
(6)
Рисунок 2 - Мультивейвлеты GHM.
Коэффициенты уравнений рескейлинга таковы:
 (6)
(6)
- I. Daubechies. Ten Lectures on Wavelets. SIAM, 1992.
- C.K.Chui. Wavelets: a tutorial in theory and applications, Academic Press, 1992.
- IEEE Trans. on Information Theory, Vol. 38, No. 2, March 1992 (специальный номер по вейвлетам)
- P.Burt, E.Adelson. The Laplacian pyramid as a compact image code, IEEE Trans. Comm., 31, pp. 482-540.
- Mark Smith, Thomas Barnwell. Exact Reconstruction Techniques for Tree-Structured Subband Coders, IEEE Trans. on ASSP, v. ASSP-34, No.3, June 1986.