Классификация известных нейросетей по основным категориям применения
На этом сайте расположена лекция, посвященная вводному курсу в тему нейронных сетей. Рассмотрены их классификация, характеристики, достоинства и недостатки. Ссылка: http://www.victoria.lviv.ua/html/oio/html/theme7_rus.htm
Тема 7. Классификация известных нейросетей по основным категориям применения
Поскольку все искусственые нейронные сети базируются на концепции нейронов, соединений и передаточных функций, существует сходство между разными структурами или архитектурами нейронных сетей. Большинство отличий зависит разных правил обучения. Рассмотрим некоторые известные модели искусственных нейросетей.
Перцептрон Розенблатта
Первой моделью нейросетей считают перцептрон Розенблатта. Теория перцептронов является основой для многих типов искусственных нейросетей прямого распространения и классикой для изучения.
Однослойный перцептрон способен распознавать простейшие образы. Отдельный нейрон вычисляет взвешенную сумму элементов входного сигнала, отнимает значение сдвига и пропускает результат через жесткую пороговую функцию, выход которой равняется +1 или -1. В зависимости от значения выходного сигнала принимается решение:
+1 - входной сигнал принадлежит классу A,
-1 - входной сигнал принадлежит классу B.
На рис. 1 показана схема нейронов, используемых в однослойных перцептронах, график передаточной функции и схема решающих областей, созданных в многомерном пространстве входных сигналов. Решающие области определяют, какие входные образы будут отнесены к классу A, какие - к классу B. Перцептрон, состоящий из одного нейрона, формирует две решающих области, разделенных гиперплоскостью. На рисунке показанный случай, когда размерность входного сигнала равняется 2. При этом разделяющая поверхность представляет собой прямую линию на плоскости. Уравнение, задающее разделяющую прямую, зависит от значений синаптических весов и сдвига.
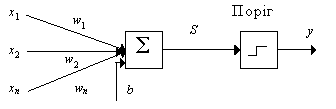
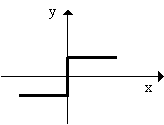

Рис. 1. Схема нейрона, график передаточной функции и разделяющая поверхность
Алгоритм обучения однослойного перцептрона
- Инициализация синаптических весов и сдвига: синаптические весы принимают небольшие случайные значения.
- Предъявление сети нового входного и желаемого выходного сигналов:
Входной сигнал x=(x1, x2, ..., xn) предъявляется нейрону вместе с желаемым выходным сигналом d. - Вычисление выходного сигнала нейрона:
- Настраивание значений весов:
- Переход к шагу 2.
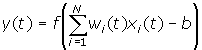
wi(t+1)=wi (t)+r[d(t)-y(t)]xi (t), i=1, ..., N
где wі(t) - - вес связи от і-го элемента входного сигнала к нейрону в момент времени t, r - скорость обучения (меньше 1); d(t) - желаемый выходной сигнал.
Если сеть принимает правильное решение, синаптические весы не модифицируются.
Тип входных сигналов: бинарные или аналоговые.
Размерности входа и выхода ограничены при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации - технологическими возможностями.
Области применения: распознавание образов, классификация.
Недостатки. Примитивные разделяющие поверхности (гиперплоскости) дают возможность решать лишь простейшие задачи распознавания.
Преимущества. Программные и аппаратные реализации модели очень просты. Простой и быстрый алгоритм обучения.
Модификации. Многослойные перцептроны дают возможность строить более сложные разделяющие поверхности и потому более распространены.
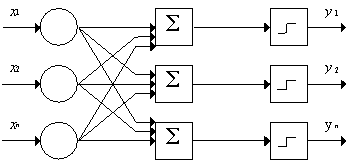
Рис. 2. Перцептрон с несколькими выходами
Нейросеть обратного распространение погрешности (Back Propagation)
Архитектура FeedForward BackPropagation была разработана в начале 1970-х лет несколькими независимыми авторами: Вербор (Werbor); Паркер (Parker); Румельгарт (Rumelhart), Хинтон (Hinton) и Вильямс (Williams). Сейчас, парадигма ВackРropagation наиболее популярная, эффективная и легкая модель обучения для сложных, многослойных сетей. Она используется в разных типах приложений и породила большой класс нейросетей с разными структурами и методами обучения.
Типичная сеть ВackРropagation имеет входной слой, выходной слой и по крайней мере один скрытый слой. Теоретически, ограничений относительно числа скрытых слоев не существует, но практически применяют один или два.

Рис. 3. Многослойный перцептрон
Нейроны организованы в послойную структуру с прямой передачей сигнала. Каждый нейрон сети продуцирует взвешенную сумму своих входов, пропускает эту величину через передаточную функцию и выдает выходное значение. Сеть может моделировать функцию практически любой сложности, причем число слоев и число нейронов в каждом слое определяют сложность функции. Определение числа промежуточных слоев и числа нейронов в них является важным при моделировании сети. Большинство исследователей и инженеров, применяя архитектуру к определенным проблемам используют общие правила, в частности:
- Количество входов и выходов сети определяются количеством входных и выходных параметров исследуемого объекта, явления, процесса, и т.п.. В отличие от внешних слоев, число нейронов скрытого слоя выбирается эмпирическим путем. В большинстве случаев достаточное количество нейронов составляет nск Ј nвх + nвых, где nвх, nвых - количество нейронов во входном и, соответственно, в выходном слоях.
- Если сложность в отношении между полученными и желаемыми данными на выходе увеличивается, количество нейронов скрытого слоя должна также увеличиться.
- Если моделируемый процесс может разделяться на много этапов, нужен дополнительный скрытый слой (слои). Если процесс не разделяется на этапы, тогда дополнительные слои могут допустить перезапоминание и, соответственно, неверное общее решение.
После того, как определено число слоев и число нейронов в любом из них, нужно найти значения для синаптических весов и порогов сети, способных минимизировать погрешность спродуцированного результата. Именно для этого существуют алгоритмы обучения, где происходит подгонка модели сети к имеющимся обучающим данным. Погрешность для конкретной модели сети определяется путем прохождения через сеть всех обучающих примеров и сравнения спродуцированних выходных значений с желаемыми значениями. Множество погрешностей создает функцию погрешностей, значение которой можно рассматривать, как погрешность сети. В качестве функции погрешностей чаще используют сумму квадратов погрешностей.
Для лучшего понимания алгоритма обучения сети Back Propagation нужно разъяснить понятия поверхности состояний. Каждому значению синаптических весов и порогов сети (свободных параметров модели количеством N) отвечает одно измерение в многомерном пространстве. N+1-ое измерение отвечает погрешности сети. Для разных соединений весов соответствующую погрешность сети можно изобразить точкой в N+1-измеримом пространстве, все эти точки образовывают некоторую поверхность - поверхность состояний. Цель обучения нейросети состоит в нахождении на многомерной поверхности наиболее низкой точки.
Поверхность состояний имеет сложное строение и довольно неприятные свойства, в частности, наличие локальных минимумов (точки, наиболее низкие в своем определенном округе, но выше глобального минимума), плоские участки, седловые точки и длинные узкие овраги. Аналитическими средствами невозможно определить расположение глобального минимума на поверхности состояний, поэтому обучение нейросети по сути состоит в исследовании этой поверхности.
Отталкиваясь от начальной конфигурации весов и порогов (от случайно избранной точки на поверхности), алгоритм обучения постепенно отыскивает глобальный минимум. Вычисляется вектор градиента поверхности погрешностей, который указывает направление кратчайшего спуска по поверхности из заданной точки. Если немножко продвинуться по нему, погрешность уменьшится. В конце концов, алгоритм останавливается в нижней точке, которая может оказаться лишь локальным минимумом (в идеальном случае - глобальным минимумом). Сложность здесь состоит в выборе длины шагов. При большой длине шага сходимость будет быстрее, но есть опасность перепрыгнуть решения, или пойти в неправильном направлении. При маленьком шаге, правильное направление будет выявлено, но возрастает количество итераций. На практике размер шага берется пропорциональным крутизне склона с некоторой константой - скоростью обучения. Правильный выбор скорости обучения зависит от конкретной задачи и определяется исследовательским путем. Эта константа может также зависеть от времени, уменьшаясь по мере продвижения алгоритма.
Алгоритм действует итеративно, его шаги называются эпохами. На каждой эпохе на вход сети поочередно подаются все обучающие примеры, выходные значения сети сравниваются с желаемыми значениями и вычисляется погрешность. Значение погрешности, а также градиента поверхности состояний используют для коррекции весов, и действия повторяются. Процесс обучения прекращается или если пройдено определенное количество эпох, или если погрешность достигает определенного уровня малости, или если погрешность перестает уменьшаться (пользователь преимущественно сам выбирает нужный критерий останова).
Алгоритм обучение сети
- Инициализация сети: весовые коэффициенты и сдвиги сети принимают малые случайные значения.
- 2. Определение элемента обучающего множества: (вход - выход). Входы (x1, x2... xN), должны различаться для всех примеров обучающего множества.
- Вычисление выходного сигнала:
- Настраивание синаптических весов:
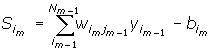
yim= f(Sjm)
im=1, 2, ..., Nm, m=1, 2, ..., L
где S - выход сумматора, w - вес связи, y - выход нейрона, b - смещение, i - номер нейрона, N - число нейронов в слое, m - номер слоя, L - число слоев, f- передаточная функцяя.
wij(t+1)=wij(t)+rgjx'і
где wij - вес от нейрона i или от элемента входного сигнала i к нейрону j в момент времени t, xi' - выход нейрона i, r - скорость обучения, gj - значение погрешности для нейрона j.
Если нейрон с номером j принадлежит последнему слою, тогда
gj=yj(1-yj)(dj-yj)
где dj - желаемый выход нейрона j, yj - поточный выход нейрона j.
Если нейрон с номером j принадлежит одному з слоев с первого по предпоследний, тогда
где k пробегает все нейроны слоя с номером на единицу больше, чем у того, которому принадлежит нейрон j.
Внешние сдвиги нейронов b настраиваются аналогичным образом.
Тип входных сигналов: целые или действительные.
Тип выходных сигналов: действительные из интервала, заданного передаточной функцией нейронов.
Тип передаточной функции: сигмоидальная. В нейронных сетях применяются несколько вариантов сигмоидальных передаточных функций.
Функция Ферми (экспонентная сигмоида):
де s - выход сумматора нейрона, a - некоторый параметр.
Рациональная сигмоида:
Гиперболический тангенс:

Упомянутые функции относятся к однопараметрическим. Значение функции зависит от аргумента и одного параметра. Также используются многопараметрические передаточные функции, например:
Сигмоидальные функции являются монотонно возрастающими и имеют отличные от нуля производные по всей области определения. Эти характеристики обеспечивают правильное функционирование и обучение сети.
Области применения. Распознавание образов, классификация, прогнозирование.
Недостатки. Многокритериальная задача оптимизации в методе обратного распространения рассматривается как набор однокритериальных задач - на каждой итерации происходят изменения значений параметров сети, которые улучшают работу лишь с одним примером обучающей выборки. Такой подход существенным образом уменьшает скорость обучения.
Преимущества. Обратное распространение - эффективный и популярный алгоритм обучения многослойных нейронных сетей, с его помощью решаются многочисленные практические задачи.
Модификации. Модификации алгоритма обратного распространения связаны с использованием разных функций погрешности, разных процедур определения направления и величины шага.
Delta Bar Delta
Delta bar Delta была разработана Робертом Джекобсом (Robert Jacobs), для улучшения оценки обучения стандартных сетей FeedForward и является модификацией сети BackPropagation
Процедура BackPropagation базируется на подходе крутого спуска, который минимизирует погрешность сети во время процесса перемены синаптических весов. Стандартные оценки обучения применяются на базисе "слой за слоем" и значение момента назначаются глобально. Моментом считается фактор, который используется для сглаживания оценки обучения. Момент прибавляется к стандартному изменению веса и пропорционален к предыдущему изменению веса. Хотя этот метод успешен в решении многих задач, сходимость процедуры слишком медленная для использования.
Delta bar Delta имеет "неформальный" подход к обучению искусственных сетей, при котором каждый вес имеет свой собственный самоадаптированный фактор обучения и прошлые значения погрешности используются для вычисления будущих значений. Знание вероятных погрешностей разрешает сети делать интеллектуальные шаги при смене весов, но процесс усложняется тем, что каждый вес может иметь совсем разное влияние на общую погрешность. Джекобс предложил понятие "здравого смысла", когда каждый вес соединения сети должна иметь собственную оценку обучения, а размер шага, который предназначен одному весу соединения не применяется для всех весов в слое.
Оценка обучения любого веса соединения изменяется на основе информации про текущую погрешность, найденной из стандартной ВackРropagation. Если локальная погрешность имеет одинаковый знак для нескольких последовательных временных шагов, оценка обучения для этого соединения линейно увеличивается. Если локальная погрешность часто изменяет знак, оценка обучения уменьшается геометрически и это гарантирует, что оценки обучения соединения будут всегда положительными. Оценкам обучения разрешено изменяться во времени.
Назначение оценки обучения к каждому соединению, разрешение этой оценке обучения неперервно изменяться с течением времени обуславливают уменьшение времени сходимости.
С разрешением разных оценок обучения для любого веса соединения в сети, поиск крутейшего спуска может не выполняться. Вместо этого, весы соединений изменяются на основе частичных производных погрешности относительно самого веса и оценки "кривизны поверхности погрешности" возле текущей точки. Изменения весов отвечают ограничению местности и требуют информацию от нейронов, с которыми они соединены.
Преимущества. Парадигма Delta Bar Delta является попыткой ускорить процесс сходимости алгоритма обратного распространения за счет использования дополнительной информации об изменении параметров и весов во время обучения.
Недостатки
- Даже небольшое линейное увеличение коэффициента может привести
к значительному росту скорости обучения, которое вызывает прыжки
в пространстве весов.
- Геометрическое уменьшение коэффициента иногда бывает недостаточно
быстрым.
Extended Delta Bar Delta
Эли Минай (Ali Minai) и Рон Вильямс (Ron Williams) разработали алгоритм Eextended Delta bar Delta, как естественное продолжение работы Джекобса. В алгоритм встраивается память с особенностью восстановления. После каждого представления обучающих данных эпохи, оценивается накопленная погрешность. Если погрешность меньше за предыдущую минимальную погрешность, весы сохраняются в памяти, как наилучшие на это время. Параметр допуска руководит фазой восстановления. В случае, если текущая погрешность превышает минимальную предыдущую погрешность, модифицированную параметром допуска, все значения весов соединений стохастично возвращаются к сохраненному в памяти наилучшего множества весов.
Направленный случайный поиск
Сеть направленного случайного поиска (Directed Random Search), использует стандартную архитектуру FeedForward, которая не базируется на алгоритме BackProragation и корректирует весы случайным образом. Для обеспечения порядка в таком процессе, к случайному шагу прибавляется компонента направления, гарантирущая направление весов к предварительно успешному направлению поиска. Влияние на нейроны осуществляется в отдельности.
Для сохранности весов внутри компактной области, где алгоритм работает хорошо, устанавливают верхнюю границу величины весов. Устанавливая границы весов большими, сеть может продолжать работать, поскольку настоящий глобальный оптимум остается неизвестным. Другой особенностью правила обучение является начальное отличие в случайном распределении весов. В большинстве коммерческих пакетов существует рекомендованное разработчиком число для параметра начального отличия.
Парадигма случайного поиска имеет несколько важных черт. Она быстрая и легкая в использовании, наилучшие результаты получаются, когда начальные веса находятся близко к наилучшим весам. Быстрой парадигма является благодаря тому, что для промежуточных нейронов погрешности не вычисляются, а вычисляется лишь выходная погрешность. Алгоритм дает эффект лишь в небольшой сети, поскольку при увеличении числа соединений, процесс обучения становится длинным и трудным.
Существует четыре ключевых компонента сети со случайным поиском. Это - случайный шаг, шаг реверсирования, направленная компонента и самокорректирующее отличие.
Случайный шаг. К любому весу прибавляется случайная величина. Все обучающее множество пропускается через сеть, создавая "погрешность предсказания". Если новая общая погрешность обучающего множества меньше чем предыдущая наилучшая погрешность предсказания, текущие значения весов, включающие случайный шаг становятся новым множеством "наилучших" весов. Текущая погрешность предсказания сохраняется как новая, наилучшая погрешность предсказания.
Шаг реверсирования. Если результаты случайного шага хуже предыдущей наилучшей, случайная величина отнимается от начального значения веса. Это создает множество весов, которые находятся в противоположном направлении к предыдущему случайному шагу. Если общая "погрешность предсказания" меньше предыдущей наилучшей погрешности, текущие значения весов и текущая погрешность предсказания сохраняются как наилучшие. Если и прямой и обратный шаги не улучшают результат, к наилучшим весам прибавляется полностью новое множество случайных значений и процесс начинается сначала.
Направленная компонента. Для сходимости сети создается множество направленных компонент, полученных по результатам прямого и обратного шагов. Направленные компоненты, которые отображают цепь успехов или неудач предыдущих случайных шагов, прибавляются к случайным компонентам на каждом шаге процедуры и обеспечивают элемент "здравого смысла" в поиске. Доказано, что добавление направленных компонент обеспечивает резкое повышение эффективности алгоритма.
Самокорректирующее отличие. Определяется параметр начального отличия для управления начальным размером случайных шагов, который прибавляется к весам. Адаптивный механизм изменяет параметр отличия, который базируется на текущей оценке успеха или неудачи. Правило обучения предполагает, что текущий размер шагов для весов в правильном направлении увеличивается для случая нескольких последовательных успехов. Наоборот, если происходит несколько последовательных неудач, отличие уменьшается для уменьшения размера шага.
Преимущества. Для небольших и средних нейросетей, направленный случайный поиск дает хорошие результаты за короткое время. Обучение автоматическое, требует небольшого взаимодействия с пользователем.
Недостатки. Количество весов соединений накладывает практические ограничения на размер задачи. Если сеть имеет больше чем 200 весов соединений, направленный случайный поиск может требовать увеличения времени обучения, но продуцировать приемлемые решения.
Нейронная сеть высшего порядка или функционально - связанная нейронная сеть
Функционально-связанные сети были разработаны Йох-Хан Пао (Yoh-Han Pao) и детально описанны в его книге "Адаптивное распознавание образов и нейронные сети" (Adaptive Pattern Recognition and Neural Networks). Нейросеть расширяет стандартную архитектуру FeedForward BackPropagation модификацией узлов на входном слое. Входы комбинируются математическим путем с помощью функций высшего порядка, таких как квадраты, кубы или синусы и расширяют восприятие сетью заданной проблемы. Из названий этих функций, высшего порядка или функционально-связанных входов и вытекает название нейросетей.
Существует два основных способа добавления входных узлов. В первом, в модель могут добавляться перекрестные произведения входных элементов, это называется входным произведением или тензорной моделью, где каждая компонента входного образа перемножается со всеми компонентами входного вектора. Например, для сети ВackРropagation с тремя входами (A, B и C), перекрестными произведениями будут AA, BB, CC, AB, AC и BC (элементы второго порядка). Также могут прибавляться элементы третьего порядка, такие как ABC.
Вторым методом для добавления входных узлов является функциональное расширение базовых входов. В случае модели с входами A, B и C, ее можно превратить в модель нейронной сети высшего порядка со входами: A, B, C, SIN(A), COS(B), LOG(C), MAX(A,B,C) и др. Полный эффект должна обеспечить сеть с объединением модели тензорного и функционального расширения.
Никакой новой информации не прибавляется, но расширенное представление входов делает сеть проще для обучения. Существуют ограничения для этой модели. Для преобразования начальных входов необходимая обработка большего количества входных узлов, влияющих на быстродействие сети, поэтому при расширении входов должно быть учтено объединение точного решения и сравнительно небольшого времени обучения.
Сеть Кохонена
Сеть разработана Тойво Кохоненом в начале 1980-х гг. и принципиально отличается от рассмотренных высше сетей, поскольку использует неконтролируемое обучение и обучающее множество состоит лишь из значений входных переменных.
Сеть распознает кластеры в обучающих данных и распределяет данные по соответствующих кластерах. Если дальше сеть встречается с набором данных, непохожим ни на одним из известных образцов, она относит его к нового кластеру. Если в данных содержатся метки классов, то сеть способна решать задачи классификации.
Сеть Кохонена имеет всего два слоя: входной и выходной, ее называют самоорганизованной картой. Элементы карты располагаются в некотором пространстве - как правило двумерном.
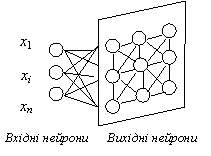
Рис. 4. Сеть Кохонена
Сеть Кохонена учится методом последовательных приближений. Начиная со случайным образом выбранного выходного расположения центров, алгоритм постепенно улучшается для кластеризации обучающих данных.
Основной итерационный алгоритм Кохонена последовательно проходит ряд эпох, на каждой эпохе обрабатывается один обучающий пример. Входные сигналы (векторы действительных чисел) последовательно предъявляются сети, желаемые выходные сигналы не определяются. После предъявления достаточного числа входных векторов, синаптические весы сети определяют кластеры. Весы организуются так, что топологически близкие узлы чувствительны к похожим входным сигналам.
Для реализации алгоритма необходимо определить меру соседства нейронов (окрестность нейрона-победителя). На рис. 6 показаны зоны топологического соседства нейронов на карте признаков в разные моменты времени. NEj(t) - множество нейронов, считающиеся соседями нейрона j в момент времени t. Зоны соседства уменьшаются с течением времени.
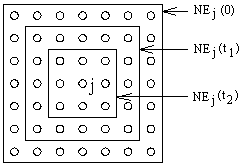
Рис. 5. Зоны топологического соседства на карте признаков в разные моменты времени
Алгоритм функціонування мережі Кохонена
- Инициализация сети. Весовым коэффициентам сети даются небольшие
случайные значения. Общее число синаптических весов - M*N (см.
рис. 4). Начальная зона соседства показана на рис. 5.
- Предъявление сети нового входного сигнала.
- Вычисление расстояния до всех нейронов сети:
- Выбор нейрона с наименьшим расстоянием:
- Настраивание весов нейрона j* и его соседей:
- Возвращение к шагу 2.
Расстояния dj от входного сигнала до каждого нейрона j определяются по формуле:
где xi - i-ый элемент входного сигнала в момент времени t, wij(t) - вес связи от i-го элемента входного сигнала к нейрону j в момент времениt.
Выбирается нейрон-победитель j*, для которого расстояние dj самое малое.
Делается настраивание весов для нейрона j* и всех нейронов из его окрестности NE. Новые значения весов:
wij(t+1)=wij(t)+r(t)(xi(t)-wij(t))
где r(t) - скорость обучения, которая уменьшается с течением времени (положительное число, меньше единицы).
В алгоритме используется коэффициент скорости обучения, которое постепенно уменьшается, для тонкой коррекции на новой эпохе. В результате центр устанавливается в определенной позиции, которая удовлетворительным образом кластеризует примеры, для которых данный нейрон является победителем.
Свойство топологической упорядоченности достигается в алгоритме с помощью использования понятия окрестности. Окрестность - это несколько нейронов, окружающих нейрон-победитель. Соответственно скорости обучения, размер окрестности постепенно уменьшается, так, что сначала к нему принадлежит довольно большое число нейронов (возможно вся карта), на самых последних этапах окрестность становится нулевой и состоит лишь из нейрона-победителя. В алгоритме обучения коррекция применяется не только к нейрону-победителю, но и к всем нейронам из его текущей окрестности. В результате такого изменения окрестности, начальные довольно большие участки сети иммигрируют в сторону обучающих примеров.
Сеть формирует грубую структуру топологического порядка, при которой похожие примеры активируют группы нейронов, которые близко находятся на топологической карте. С каждой новой эпохой скорость обучения и размер окрестности уменьшаются, и внутри участков карты обнаруживаются более тонкие расхождения, что приводит к точному настраиванию каждого нейрона. Часто обучения умышленно разбивают на две фазы: более короткую, с большой скоростью обучения и больших окресностей, и более продолжительную с маленькой скоростью обучения и нулевыми или почти нулевыми окрестностями.
После того, как сеть научена распознаванию структуры данных, ее можно использовать как средство визуализации при анализе данных.
Области применения. Кластерный анализ, распознавание образов, классификация.
Недостатки. Сеть может быть использована для кластерного анализа только в том случае, если заранее известное число кластеров.
Преимущества. Сеть Кохонена способна функционировать в условиях препятствий, так как число кластеров фиксировано, весы модифицируются медленно, настраивание весов заканчивается после обучения.
Модификации. Одна из модификаций состоит в том, что к сети Кохонена прибавляется сеть MAXNET, что определяет нейрон с наименьшим расстоянием ко входному сигналу.
Квантование обучающего вектора (Learning VectorQuantization)
Сеть была предложена Тойво Кохоненом в середине 80-х гг., позже, чем его работа по самоорганизованным картам. Сеть базируется на слое Кохонена, способному к сортировке примеров в соответствующие кластеры и используется как для проблем классификации, так и для кластеризации изображений.
Сеть содержит входной слой, самоорганизованную карту Кохонена и выходной слой. Пример сети изображен на рис. 6. Выходной слой имеет столько нейронов, сколько есть отличных категорий или классов. Карта Кохонена имеет ряд нейронов, сгруппированных для любого из этих классов, количество которых зависит от сложности отношения "вход-выход". Конечно, каждый класс будет иметь одинаковое количество элементов по всему слою. Слой Кохонена учится классификации с помощью обучающего множества. Сеть использует правила контролируемого обучения. Входной слой содержит столько нейронов, сколько имеется отдельных входных параметров.
Квантование обучающего вектора классифицирует свои входные данные в определенные группирования, то есть отображает n-измеримое пространство в m-измеримое пространство (берет n входов и создает m выходов). Карты сохраняют отношения между близкими соседями в обучающем множестве так, что входные образы, которые не было предварительно изучены, будут распределены по категориям их ближайших соседей в обучающих данных.
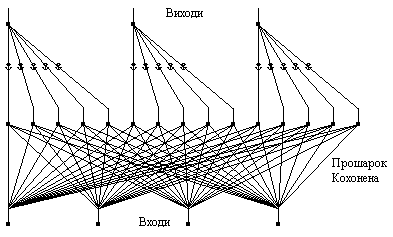
Рис. 6. Пример сети с квантованием обучающего вектора
В режиме обучения, контролируемая сеть использует слой Кохонена, где вычисляется расстояние от обучающего вектора до любого нейрона и ближайший нейрон объявляется победителем. Существует лишь один победитель на весь слой. Победителю разрешено возбуждать лишь один выходной нейрон, объявляя класс или кластер к которому принадлежит входной вектор. Если нейрон-победитель находится в ожидаемом классе обучающего вектора, его весы усиливаются в направлении обучающего вектора. Если нейрон-победитель не находится в классе обучающего вектора, весы соединений уменьшаются. Эта последняя операция упоминается как отталкивание (repulsion). Во время обучения отдельные нейроны, которые приписаны к частичному классу мигрируют к области, связанной с их специфическим классом.
Во время режима функционирования, вычисляется расстояние от входного вектора к любому нейрону и снова ближайший нейрон объявляется победителем. Это в свою очередь генерирует один выход, определяя частичный класс, найденный сетью.
Недостатки. Для сложной классификации похожих входных примеров, сеть требует большой карты Кохонена с большим количеством нейронов на класс. Это может быть преодолено целесообразным выбором обучающих примеров или расширением входного слоя.
Некоторые нейроны имеют тенденцию к победе слишком часто, то есть настраивают свои веса очень быстро, в то время как другие постоянно остаются незадействованными. Это часто случается, если их веса имеют значения далекие от обучающих примеров. Для устранения этого, нейрон, который побеждает слишком часто штрафуется, то есть уменьшаются весы его связей с каждым входным нейроном. Это уменьшения весов пропорционально к разности между частотой побед нейрона и частотой побед среднего нейрона.
Преимущества. Алгоритм предельной коррекции используется для усовершенствования решения даже если было найдено относительно хорошее решение. Алгоритм способен действовать, если нейрон-победитель находится в неправильном классе, а второй наилучший нейрон в правильном классе. Обучающий вектор должен быть близко от средней точки пространства, соединяющего эти два нейрона. Неправильный нейрон-победитель смещается из обучающего вектора, а нейрон из другого места продвигается к обучающему вектору. Эта процедура делает четкой границу между областями, где возможна неверная классификация.
В начале обучения желательно отключить отталкивание. Нейрон-победитель продвигается к обучающему вектору лишь тогда, когда обучающий вектор и нейрон-победитель находятся в одном классе. Такой подход целесообразен, если нейрон должен обойти область, имющую отличный класс для достижения необходимой области.
Сеть встречного распространения (CounterРropagation)
Роберт Хехт-Нильсен (Robert Hecht-Nielsen) разработал сеть СounterРropagation как средство для объединения неконтролируемого слоя Кохонена с контролируемым выходным слоем. Сеть предназначена для решения сложных классификаций, при минимизации числа нейронов и времени обучения. Обучение для сети СounterРropagation похоже на сети с квантованием обучающего вектора.
Пример сети изображен на рис. 7. Однонаправленная сеть CounterPropagation имеет три слоя: входной слой, самоорганизованная карта Кохонена и выходной слой, использующий правило "дельта" для изменения входных весов соединений. Этот слой называют слоем Гроссберга.
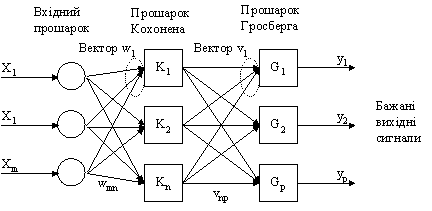
Рис. 7. Сеть встречного распространения без обратных связей
Первая сеть СounterРropagation состояла из двухнаправленного отображения между входным и выходным слоями. Данные поступают на входной слой для генерации классификации на выходном слое, выходной слой поочередно принимает дополнительный входной вектор и генерирует выходную классификацию на входном слое сети. Из-за такого встречно-распространенного потока информации сеть получила свое название. Много разработчиков используют однонаправленный вариант СounterРropagation, когда существует лишь один путь прямого распространения от входного к выходному слою.
В сети встречного распространения объединены два алгоритма: самоорганизованная карта Кохонена и звезда Гроссберга (Grossberg Outstar). Нейронные сети, объединяющие разные нейропарадигми как строительные блоки, более близки к мозгу по архитектуре, чем однородные структуры. Считается, что в мозгу именно каскадные соединения модулей разной специализации позволяют выполнять необходимые вычисления. Каждый элемент входного сигнала подается на все нейроны слоя Кохонена. Весы связе (wmn) образовывают матрицу W. Каждый нейрон слоя Кохонена соединен со всеми нейронами слоя Гроссберга. Весы связей (vnp) образовывают матрицу весов V.
В процессе обучения сети встречного распространения входные векторы ассоциируются с соответствующими выходными векторами (двоичными или аналоговыми). После обучения сеть формирует выходные сигналы, которые отвечают входным сигналам. Обобщающая способность сети дает возможность получать правильный выход, когда входной вектор неполный или искаженный.
Обучение сети
В результате самообучения слой приобретает способность разделять непохожие входные векторы. Какой именно нейрон будет активироваться при предъявлении конкретного входного сигнала, заранее тяжело предусмотреть.
При обучении слоя Кохонена на вход подается входной вектор и вычисляются его скалярные произведения с векторами весов всех нейронов.
Скалярное произведение является мерой сходства между входным вектором и вектором весов. Нейрон с максимальным значением скалярного произведения считается "победителем" и его весы усиливаются (весовой вектор приближается к входному).
wн=wc+r(x-wc)
где wн - новое значение веса, который соединяет входной компонент x с выигравшим нейроном, wс - предыдущее значение веса, r - коэффициент скорости обучения, которое сначала обычно равняется 0.7 и может постепенно уменьшаться в процессе обучения. Это позволяет делать большие начальные шаги для быстрого грубого обучения и меньшие шаги при подходе к окончательной величине.
Каждый вес, связанный с нейроном-победителем Кохонена, изменяется пропорционально разности между его величиной и величиной входа, к которому он присоединен. Направление изменения минимизирует разность между весом и соответствующим элементом входного слоя.
Обучающее множество может содержать много похожих между собой входных векторов, и сеть должна быть наученной активировать один нейрон Кохонена для любого из них. Весы этого нейрона является усреднением входных векторов, что его активируют.
Выходы слоя Кохонена подаются на входы нейронов слоя Гроссберга. Входы нейронов вычисляются как взвешенная сумма выходов слоя Кохонена. Каждый вес корректируется лишь в том случае, если она соединенная с нейроном Кохонена, что имеет ненулевой выход. Величина коррекции весов пропорциональна разности между весом и необходимым выходом нейрона Гроссберга. Обучение слоя Гроссберга - это обучения "с учителем", алгоритм использует заданные желаемые выходы.
Функціонування мережі
В своей простейшей форме слой Кохонена функционирует по правилу "победитель получает все". Для данного входного вектора один и только один нейрон Кохонена выдает логическую единицу, все другие выдают нуль. Слой Гроссберга функционирует в похожей манере. Его выход является взвешенной суммой выходов слоя Кохонена. Если слой Кохонена функционирует так, что лишь один выход равняется единице, а другие равняются нулю, то каждый нейрон слоя Гроссберга выдает величину веса, который связывает этот нейрон с единственным нейроном Кохонена, чей выход отличен от нуля.
В полной модели сети встречного распространения есть возможность получать выходные сигналы по входным и наоборот. Этим двум действиям отвечают прямое и обратное распространения сигналов.
Области применения. Распознавание образов, восстановление образов (ассоциативная память), сжатие данных (с потерями).
Недостатки. Сеть не дает возможности строить точные аппроксимации (точные отображения). В этом сеть значительно уступает сетям с обратным распространением погрешности. К недостаткам модели также следует отнести слабый теоретический базис модификаций сети встречного распространения.
Преимущества
- Сеть встречного распространения проста. Она дает возможность
получать статистические свойства из множества входных сигналов.
Кохонен доказал, что для наученной сети вероятность того, что
случайно выбранный входной вектор будет ближайшим к любому заданному
весовому вектору, равняется 1/k, k - число нейронов Кохонена.
- Сеть быстро учится. Время обучения по сравнению с обратным распространением
может быть в 100 раз меньше.
- По своим возможностям строить отображения сеть встречного распространения
значительно превосходит однослойные перцептроны.
- Сеть полезна для приложений, где нужна быстрая начальная аппроксимация.
- Сеть дает возможность строить функцию и обратную к ней, что находит применение при решении практических задач.
Модификации. Сети встречного распространения могут различаться способами определения начальных значений синаптических весов.
- Для повышения эффективности обучения применяется добавление шума ко входным векторам.
- Еще один метод повышения эффективности обучения - предоставление каждому нейрону "чувства справедливости". Если нейрон становится победителем чаще, чем 1/k (k - число нейронов Кохонена), то ему временно увеличивают порог, давая тем самим учиться и другим нейронам.
- Кроме "метода аккредитации", при котором для каждого
входного вектора активируется лишь один нейрон Кохонена, может
быть использован "метод интерполяции", при использовании
которого целая группа нейронов Кохонена, имеющих наибольшие выходы,
может передавать свои выходные сигналы в слой Гроссберга. Этот
метод повышает точность отображений, реализованных сетью.
Вероятностная нейронная сеть.
Вероятностная нейронная сеть была разработана Дональдом Спехтом (Donald Specht). Эта сетевая архитектура была впервые представлена в двух статьях : "вереятностные нейронные сети для классификации" (Probabilistic Neural Networks for Classification) 1988, "Отображение или ассоциативная память и вереятностные нейронные сети" (Mapping or Associative Memory and Probabilistic Neural Networks) 1990 г.
Выходы сети можно интерпретировать, как оценки вероятности принадлежности элементу к определенному классу. Вероятностная сеть учится оценивать функцию плотности вероятности, ее выход рассматривается как ожидаемое значение модели в данной точке пространства входов. Это значения связано с плотностью вероятности общего распределения входных и выходных данных.
Задача оценки плотности вероятности относится к области байесовской статистики. Обычная статистика по заданной модели показывает, какова вероятность того или другого выхода (например, на игральной кости 6 очков будет выпадать в среднем в одном случае с шести). Байесовская статистика интерпретирует по другому: правильность модели оценивается по имеющимся достоверным данным, то есть дает возможность оценивать плотность вероятности распределения параметров модели по имеющимся данным.
При решении задач классификации можно оценить плотность вероятности для каждого класса, сравнить между собой вероятности принадлежности к разным классам и выбрать модель с параметрами, при которых плотность вероятности будет большей.
Оценка плотности вероятности в сети основана на ядерных оценках. Если пример расположен в данной точке пространства, тогда в этой точке есть определенная плотность вероятности. Кластеры из рядом расположенных точек, свидетельствуют, что в этом месте плотность вероятности большая. Возле наблюдения имеется большее доверие к уровню плотности, а по мере отдаления от него доверие уменьшается и стремится к нулю. В методе ядерных оценок в точке, которая отвечает каждому примеру, помещается некоторая простая функция, потом они все прибавляются и в результате получается оценка для общей плотности вероятности. Чаще в качестве ядерных функций берут колоколоподобные функции (гауссовские). Если имеется достаточное количество обучающих примеров, такой метод дает хорошие приближения к истинной плотности вероятности.
Вероятностная сеть имеет три слоя: входной, радиальный и выходной. Радиальные элементы берутся по одному на каждый пример. Каждый из них имеет гауссовскую функцию с центром в этом примере. Каждому классу отвечает один выходной элемент. Выходной элемент соединен лишь с радиальными элементами, относящихся к его классу и подытоживает выходы всех элементов, принадлежащих к его классу. Значения выходных сигналов получаются пропорционально ядерным оценкам вероятности принадлежности соответствующим классам.
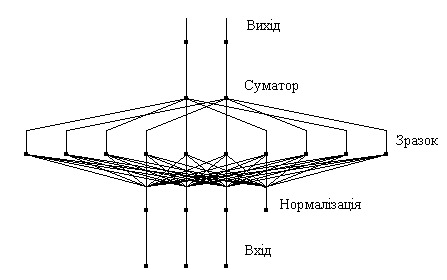
Рис. 8. Приклад імовірнісної нейронної мережі
Преимущества. Обучение вероятностной нейронной сети намного проще, чем ВackРropagation. Недостатком сети является ее размер, поскольку она фактически содержит в себе все обучающие данные, требует много памяти и может медленно работать.
Модификации. Базовая модель вероятностной нейронной сети имеет модификации. Предположим, что пропорции классов в обучающем множестве отвечают их пропорциям во всем исследуемом множестве (априорная вероятность). Например, если среди всех людей больными являются 2%, то в обучающем множестве для сети, диагностирующей заболевание, больных также должно быть 2%. Если же априорные вероятности отличаются от пропорции в обучающей выборке, сеть будет выдавать неверный результат. Это можно учесть, вводя корректирующие коэффициенты для разных классов.
Сеть Хопфилда
Джон Хопфилд впервые представил свою ассоциативную сеть в 1982 г. в Национальной Академии Наук. В честь Хопфилда и нового подхода к моделированию, эта сетевая парадигма упоминается как сеть Хопфилда. Сеть базируется на аналогии физики динамических систем. Начальные применения для этого вида сети включали ассоциативную, или адресованную по смыслу память и решали задачи оптимизации.
Сеть Хопфилда использует три слоя: входной, слой Хопфилда и выходной слой. Каждый слой имеет одинаковое количество нейронов. Входы слоя Хопфилда подсоединены к выходам соответствующих нейронов входного слоя через изменяющиеся веса соединений. Выходы слоя Хопфилда подсоединяются ко входам всех нейронов слоя Хопфилда, за исключением самого себя, а также к соответствующим элементам в выходном слое. В режиме функционирования, сеть направляет данные из входного слоя через фиксированные веса соединений к слою Хопфилда. Слой Хопфилда колебается, пока не будет завершено определенное количество циклов, и текущее состояние слоя передается на выходной слой. Это состояние отвечает образу, уже запрограммированному в сеть.
Обучение сети Хопфилда требует, чтобы обучающий образ был представлен на входном и выходном слоях одновременно. Рекурсивный характер слоя Хопфилда обеспечивает средства коррекции всех весов соединений. Недвоичная реализация сети должна иметь пороговый механизм в передаточной функции. Для правильного обучение сети соответствующие пары "вход-выход" должны отличаться между собой.
Если сеть Хопфилда используется как память, адресуемая по смыслу она имеет два главных ограничения. Во-первых, число образов, которые могут быть сохранены и точно воспроизведены является строго ограниченным. Если сохраняется слишком много параметров, сеть может сходится к новому несуществующему образу, отличному от всех запрограммированных образов, или не сходится вообще.
Граница емкости памяти для сети приблизительно 15% от числа нейронов в слое Хопфилда. Вторым ограничением парадигмы есть то, что слой Хопфилда может стать нестабильным, если обучающие примеры являются слишком похожими. Образец образа считается нестабильным, если он применяется за нулевое время и сеть сходится к некоторому другому образу из обучающего множества. Эта проблема может быть решена выбором обучающих примеров более ортогональных между собой.
Структурная схема сети Хопфилда приведена на рис. 9.
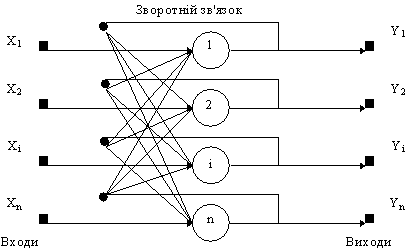
Рис. 9. Структурная схема сети Хопфилда
Задача, решаемая данной сетью в качестве ассоциативной памяти, как правило, формулируется так. Известен некоторый образцовый набор двоичных сигналов (изображений, звуковых оцифровок, других данных, которые описывают определенные объекты или характеристики процессов). Сеть должна уметь с зашумленого сигнала, представленного на ее вход, выделить ("припомнить" по частичной информации) соответствующий образец или "дать вывод" о том, что входные данные не отвечают ни одному из образцов. В общем случае, любой сигнал может быть описан вектором x1, хі, хn..., n - число нейронов в сети и величина входных и выходных векторов. Каждый элемент xi равняется или +1, или -1. Обозначим вектор, который описывает k-ий образец, через Xk, а его компоненты, соответственно, - xik, k=0, ..., m-1, m - число образцов. Если сеть распознает (или "вспоминает") определенный образец на основе предъявленных ей данных, ее выходы будут содержать именно его, то есть Y = Xk, где Y - вектор выходных значений сети: y1, yi, yn. В противном случае, выходной вектор не совпадет ни с одним образцом.
Если, например, сигналы представляют собой какое-то изображение, то, отобразив в графическом виде данные с выхода сети, можно будет увидеть картинку, которая целиком совпадает с одной из образцовых (в случае успеха) или же "свободную импровизацию" сети (в случае неудачи).
Алгоритм функционирования сети
- На стадии инициализации сети синаптические коэффициенты устанавливаются таким образом:
- На входы сети подается неизвестный сигнал. Его распространение непосредственно устанавливает значения выходов:
- Рассчитывается новое состояние нейронов
- Проверяем изменились ли выходные значения выходов за последнюю итерацию. Если да - переход к пункту 2, иначе (если выходы стабилизировались) - конец. При этом выходной вектор представляет собой образец, что лучше всего отвечает входным данным.
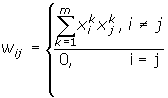
Здесь i и j - индексы, соответственно, предсинаптического и постсинаптического нейронов; xik, xjk - i-ый і j-ый элементы вектора k-ого образца.
yi(0) = xi , i = 0...n-1,
поэтому обозначения на схеме сети входных сигналов в явном виде носит чисто условный характер. Нуль в скобке yi означает нулевую итерацию в цикле работы сети.
и новые значения выходов
где f - передаточная функция в виде пороговой, приведена на рис. 10.

Рис. 10. Передаточные функции
Иногда сеть не может провести распознавания и выдает на выходе несуществующий образ. Это связано с проблемой ограниченности возможностей сети. Для сети Хопфилда число запомненых образов m не должно превышать величины, приблизительно равной 0.15*n. Кроме того, если два образа А і Б сильно похожи, они, возможно, будут вызвать в сети перекрестные ассоциации, то есть предъявление на входы сети вектора А приведет к появлению на ее выходах вектора Б и наоборот. Благодаря итерационному алгоритму, машина продвигается к наилучшему решению
Машина Больцмана
Машина Больцмана (Boltzmann mashine) похожа по функции и действию на сеть Хопфилда и включает понятие "моделированного отжига" для поиска в пространстве состояний слоя образов глобального минимума.
Экли (Ackley), Хинтон (Hinton) и Сейновски (Sejnowski) разработали правило больцмановского обучения в 1985 г. Подобно сети Хопфилда, машина Больцмана имеет пространство состояний, которое базируется на весах соединений в слое образов. Процессы обучение сети, наполненной образами, включает сглаживание рельефа пространства состояний.
Машина Больцмана моделирует отжиг металла, который прибавляется к процессу обучение сети. Как и при физическом отжиге, температура начинается с больших значений и уменьшается с течением времени. Увеличенная температура прибавляет увеличенный шумовой коэффициент к любому нейрону в слое образов. Преимущественно, конечной температурой будет нуль. Для достижения оптимального решения целесообразно на низших температурах прибавлять больше итераций.
Машина Больцмана, учась на высокой температуре, ведет себя как случайная модель, а на низких температурах она как детерминированная. Из-за случайной компоненты в отжиговом обучении, нейрон может принять новое значение состояния, которое увеличивается быстрее, чем уменьшается общее пространство состояний. Имитация физического отжига позволяет продвигаться к глобальному минимуму, избегая локальный.
Как и в сети Хопфилда, сети может быть представлен частичный образ для восстановления отсутствующей информации. Ограничение на число классов менее 15 % от общего количества элементов в слое образов, все еще применяется.
Алгоритм функционирования сети
- Определить переменную T, представляющую искусственную температуру.
- Предъявить сети множество входов и вычислить выходы и целевую
функцию.
- Дать случайное изменение весам и пересчитать выход сети и изменение
целевой функции в соответствии с изменением весов.
- Если целевая функция уменьшилась, тогда новое множество весов
сохраняется.
Если изменение весов приводит к увеличению целевой функции, то вероятность сохранения этого изменения вычисляется по помощи распределения Больцмана:
где P(c) - вероятность изменения c в целевой функции; k - константа, аналогичная константе Больцмана, выбирается в зависимости от задачи; T - искусственная температура.
Выбирается случайное число r из равномерного распределения от нуля до единицы. Если P(c) больше, чем r, то изменение сохраняется, в противном случае величина веса возвращается к предыдущему значению.
Эта процедура дает возможность системе делать случайный шаг в направлении, портящем целевую функцию, позволяя ей вырываться из локальных минимумов.
Шаги 3 и 4 повторяются для всех весов сети, постепенно уменьшая температуру T, пока не будет достигнуто допустимое низкое значение целевой функции. В этот момент предъявляется другой входной вектор и процесс обучения повторяется. Сеть учится на всех векторах обучающего множества, пока целевая функция не станет допустимой для всех из них.
Скорость уменьшения температуры должна быть обратно пропорциональная логарифму времени. При этом сеть сходится к глобальному минимуму.
Области применения. Распознавание образов, классификация.
Недостатки. Медленный алгоритм обучения.
Преимущества. Алгоритм дает возможность сети выбираться из локальных минимумов адаптивного рельефа пространства состояний.
Модификации. Случайные изменения могут проводиться не только для отдельных весов, но и для всех нейронов слоев в многослойных сетях или для всех нейронов сети одновременно. Эти модификации алгоритма дают возможность сократить общее число итераций обучения.
Сеть Хемминга
Сеть Хемминга (Hamming) - расширение сети Хопфилда. Эта сеть была разработана Ричардом Липпманом (Richard Lippman) в середине 80-х гг. Сеть Хемминга реализует классификатор, базирующийся на наименьшей погрешности для векторов двоичных входов, где погрешность определяется расстоянием Хемминга. Расстояние Хемминга определяется как число бит, отличающихся между двумя соответствующими входными векторами фиксированной длины. Один входной вектор является незашумленым примером образа, другой - испорченным образом. Вектор выходов обучающего множества является вектором классов, к которым принадлежат образы. В режиме обучения входные векторы распределяются по категориям, для которых расстояние между образцовыми входными векторами и текущим входным вектором является минимальным.
Сеть Хемминга имеет три слоя: входной слой с количеством узлов, сколько имеется отдельных двоичных признаков; слой категорий (слой Хопфилда), с количеством узлов, сколько имеется категорий или классов; выходной слой, который отвечает числу узлов в слое категорий.
Сеть есть простой архитектурой прямого распространения с входным уровнем, полностью подсоединенным к слою категорий. Каждый элемент обработки в слое категорий является обратно подсоединенным к каждому нейрону в том же самом слое и прямо подсоединенным к выходному нейрону. Выход из слоя категорий к выходному слою формируется через конкуренцию.
Обучение сети Хемминга похоже на методологию Хопфилда. На входной слой поступает желаемый обучающий образ, а на выход выходного слоя поступает значение желаемого класса, к которому принадлежит вектор. Выход содержит лишь значение класса к которому принадлежит входной вектор. Рекурсивный характер слоя Хопфилда обеспечивает средства коррекции всех весов соединений.
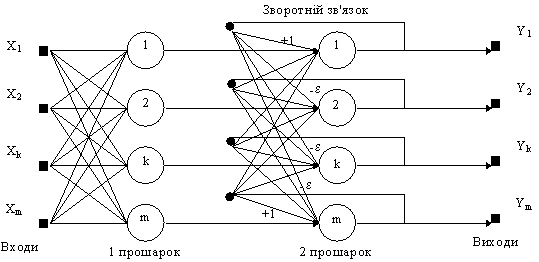
Рис. 11. Структурная схема сети Хемминга
Алгоритм функционирования сети Хемминга
- На стадии инициализации весовым коэффициентам первой слоя и порогу передаточной функции присваиваются такие значения:
- На входы сети подается неизвестный вектор x1, xi, xn ... Рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя):
- Вычисляются новые состояния нейронов второго слоя:
- Проверяется, изменились ли выходы нейронов второго слоя за последнюю
итерацию. Если да - перейти к шагу 3. Иначе - конец.
Wik=xIk/2, i=0...n-1, k=0...m-1
bk = n / 2, k = 0...m-1
Здесь xik - i-ый элемент k-ого образца.
Весовые коэффициенты тормозящих синапсов в втором слое берут равными некоторой величине 0 < v < 1/m. Синапс нейрона, связанный с его же выходом имеет вес +1.
После этого получения значения инициализируют значения выходов второго слоя:
yj(2) = yj(1), j = 0...m-1
и значения их выходов:
Передаточная функция f имеет вид порога, причем величина b должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению.
Роль первой слоя является условной: воспользовавшись один раз на первом шаге значениями его весовых коэффициентов, сеть больше не возвращается к нему, поэтому первый слой может быть вообще исключен из сети.
Сеть Хемминга имеет ряд преимуществ над сетью Хопфилда. Она способна найти минимальную погрешность, если погрешности входных бит являются случайными и независимыми. Для функционирования сети Хемминга нужно меньшее количество нейронов, поскольку средний слой требует лишь один нейрон на класс, вместо нейрона на каждый входной узел. И, в конце концов, сеть Хемминга не страдает от неправильных классификаций, которые могут случиться в сети Хопфилда. В целом, сеть Хемминга быстрее и точнее, чем сеть Хопфилда.
Двунаправленная ассоциативная память
Эта сетевая модель была разработана Бартом Козко (Bart Kosko) и расширяет модель Хопфилда. Множество парных образов учится за образами, которые представлены как биполярные векторы. Подобно сети Хопфилда, когда представляется зашумленная версия одного образа, определяется ближайший образ, ассоциированный с ним.
На рис. 12 показан пример двунаправленной ассоциативной памяти. Она имеет столько входов, сколько есть выходов. Два скрытых слоя помещаются на двух отдельных ассоциативных элементах памяти и представляют удвоенный размер входных векторов. Средние слои полностью соединены между собой. Входной и выходной слои нужны для реализации средств ввода и воссоздания информации из сети.
Средние слои разработаны для сохранности ассоциированных пар векторов. Если на вход сети поступает зашумленный вектор образа, средние слои колебаются до достижения стабильного состояния равновесия, что отвечает ближайшей наученной ассоциации и на выходе генерируется образ из обучающего множества. Подобно сети Хопфилда, двунаправленная ассоциативная память предрасположена к неправильному отыскиванию наученного образа, если поступает неизвестный входной вектор, который не был в составе обучающего множества.
Двунаправленная ассоциативная память относится к гетероассоциативной памяти. Входной вектор поступает на один набор нейронов, а соответствующий выходной вектор продуцируется на другом наборе нейронов. Входные образы ассоциируются с выходными.
Для сравнения: сеть Хопфилда автоассоциативная. Входной образ может быть восстановлен или выправлен сетью, но не может быть ассоциирован с другим образом. В сети Хопфилда используется однослойная структура ассоциативной памяти, в которой выходной вектор появляется на выходе тех же нейронов, на которые поступает входной вектор.
Двунаправленная ассоциативная память, как и сеть Хопфилда, способна к обобщению, вырабатывая правильные выходные сигналы, несмотря на поврежденные входы.
Рассмотрим схему двунаправленной ассоциативной памяти. Входной вектор A обрабатывается матрицей весов W сети, в результате чего продуцируется вектор выходных сигналов сети B. Вектор B обрабатывается транспонированной матрицей WT весов сети, которая продуцирует сигналы, представляющие новый входной вектор A. Этот процесс повторяется до тех пор, пока сеть не достигнет стабильного состояния, в котором ни вектор A, ни вектор B не изменяются.
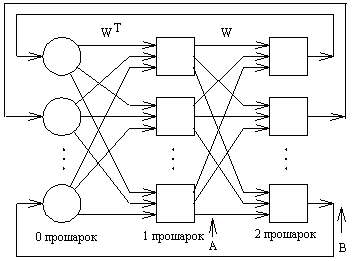
Рис. 12. Двухнаправленная ассоциативная память
Нейроны в слоях 1 и 2 функционируют, как и в других парадигмах, вычисляя сумму взвешенных входов и значения передаточной функции F:
или в векторной форме:
B=F(AW)
где B - вектор выходных сигналов нейронов слоя 2, A - вектор выходных сигналов нейронов слоя 1, W - матрица весов связей между слоями 1 и 2, F - передаточная функция.
Аналогічно
A=F(BWT),
где WT является транспозицией матрицы W.
В качестве передаточной функции используется экспонентная сигмоида.
Слой 0 не делает вычислений и не имеет памяти. Он - лишь средством распределения выходных сигналов слоя 2 к элементам матрицы WT.
Формула для вычисления значений синаптических весов:
где Aj и Bj - входные и выходные сигналы обучающего множества.
Весовая матрица вычисляется как сумма произведений всех векторных паров обучающего множества.
Системы с обратной связью имеют тенденцию к колебаниям. Они могут переходить от состояния к состоянию, никогда не достигая стабильности. Доказано, что двунаправленная ассоциативная память безусловно стабильна при любых значениях весов сети.
Области применения. Ассоциативная память, распознавание образов.
Недостатки. Емкость двунаправленной ассоциативной памяти жестко ограничена. Если n - количество нейронов во входном слое, то число векторов, которые могут быть запомнены в сети не превышает L=n/2log2n. Так, если n=1024, то сеть способна запомнить не более 25 образов.
Двунаправленная ассоциативная память имеет некоторую непредсказуемость в процессе функционирования, возможные ошибочные ответы.
Преимущества
- По сравнению с автоассоциативной памятью (например, сетью Хопфилда),
двунаправленная ассоциативная память дает возможность строить
ассоциации между векторами A и B, что в общем случае имеют разные
размерности. За счет таких возможностей гетероассоциативная память
имеет более широкий класс применений, чем автоассоциативная память.
- Двунаправленная ассоциативная память - простая сеть, которая
может быть реализована в виде отдельной СБИС или оптоэлектронным
способом.
- Процесс формирования синаптических весов простой и быстрый.
Сеть быстро сходится в процессе функционирования.
- Сигналы в сети могут быть как дискретными, так и аналоговыми. Для обоих случаев доказана стабильность сети.
Сеть адаптивной резонансной теории
Разработана Стивеном Гроссбергом и Карпентером в середине 80-х гг. Парадигма использует неконтролируемое обучение, анализирует значимые входные данные, выявляет возможные признаки и классифицирует образы в входном векторе.
Сеть адаптивной резонансной теории состоит из двух взаимосвязанных слоев нейронов, расположенных между входным и выходным слоями. Каждый входной образ низшей слоя резонанса стимулирует ожидаемый образ на высшем слое, который пересылается к низшему слою, чтобы влиять на следующий вход. Это создает "резонанс" между низшим и высшим слоями для облегчения сетевой адаптации образов.
Сеть преимущественно используется в биологическом моделировании, тем не менее существуют некоторые технические применения. Главным ограничением сетевой архитектуры является ее шумовая чувствительность. Даже небольшое количество шума на входном векторе путает обобщающие возможности наученной сети.
Сеть ART-1 реализует алгоритм кластеризации, очень похожий на алгоритм "последовательного лидера". Следуя этому алгоритму первый входной сигнал считается образцом первого кластера. Следующий входной сигнал сравнивается с образцом первого кластера. Говорят, что входной сигнал "направляется за лидером" и принадлежит первому кластеру, если расстояние до образца первого кластера меньше порога. В противном случае второй входной сигнал - образец второго кластера. Этот процесс повторяется для всех следующих входных сигналов. Таким образом, число кластеров растет с течением времени и зависит как от значения порога, так и от метрического свидетельства расстояния, используемое для сравнения входных сигналов и образцов классов.
Основная часть сети ART-1 похожа на сеть Хемминга. С помощью последовательных связей вычисляется соответствие входных сигналов и образцов кластеров. Максимальное значение соответствия усиливается с помощью латеральных связей выходных нейронов.
Сеть ART-1 отличается от сети Хемминга обратными связями от выходных нейронов к входным, кроме того есть возможность выключать выходной нейрон с максимальным значением соответствия и проводить тестирования соответствия входного сигнала и образцов кластеров, как того требует алгоритм "последовательного лидера".

Рис. 13. Основные компоненты классификатора Карпентер/Гроссберга
Алгоритм функционирования сети
- Инициализация сети:
- Предъявление сети нового бинарного входного сигнала:
- Вычисление значений соответствия:
- Выбор образца с наибольшим соответствием:
- Сравнение с порогом:
- Исключение примера с наибольшим значением соответствия:
- Адаптация примера с наибольшим значением соответствия:
- Включение всех исключенных на шаге 6 образцов. Возвращение к шагу 2.
vij(0)=1;Wij(0)=1/(1+N)
0Ј i Ј N-1; 0Ј j Ј M-1; 0Ј b Ј 1;
где wij(t) - синаптический вес связи от i-го нейрона первого слоя к j-го нейрону второго слоя в момент времени t, vij(t) - синаптический вес связи от j-го нейрона второго слоя к i-го нейрону первого слоя в момент времени t, b - значение порога.
Весы vij(t) і wij(t) определяют образец, отвечающий нейрону j.
Порог b показывает, насколько должен входной сигнал совпадать с одним из запомненных образцов, чтобы они считались похожими. Близкое к единице значения порога требует почти полного совпадения.
При небольших значениях порога входной сигнал и образец, даже, если они сильно различаются, считаются принадлежащими к одному кластеру.
Входные сигналы предъявляются выходному слою нейронов аналогично сети Хемминга.
Значение соответствия вычисляются параллельно для всех образцов, запомненых в сети, аналогично сети Хемминга.
yj=max(yj)
Эта операция выполняется с помощью латерального торможения.
 ;
;

если
 переход
к шагу 7, иначе к шагу 6.
переход
к шагу 7, иначе к шагу 6.
На этом шаге вычисляется отношение скалярного произведения входного сигнала и образца с наибольшим значением соответствия к числу единичных бит входного сигнала. Значение отношения сравнивается с порогом, введенном на первом шаге.
Если значение отношения больше порога, то входной сигнал считается похожим наподобие наибольшему значению соответствия. В этом случае образец модифицируется путем выполнения операции AND (логическое "И"). Новый образец является образцом на предыдущем шаге + входной сигнал.
Если значение отношения меньше порога, то считается, что входной сигнал отличается от всех образцов и рассматривается как новый образец. В сеть вводится нейрон, отвечающий новому образцу, и вычисляются значение синаптических весов.
Выход нейрона с наибольшим значением соответствия временно устанавливается равным нулю и более не принимает участия в шаге 4.
vij(t+1)=vij(t)xj

Входные сигналы в этой модели бинарные.
Размерности входа и выхода ограничены при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации - технологическими возможностями.
Емкость сети совпадает с числом нейронов второго слоя и может увеличиваться в процессе функционирования сети.
Области применения. Распознавание образов, кластерный анализ.
Недостатки. Неограниченное увеличение числа нейронов в процессе функционирования сети. В появлением шума возникают значительные проблемы, связанные с неконтролируемым ростом числа образцов.
Преимущества. Обучение без учителя.
Модификации. Существует модель ART-2 с аналоговыми значениями входными сигналами.