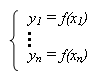Регрессионный анализ. Градуировка.

Автор: А.В. Гармаш

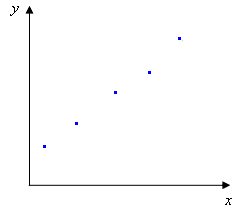
Проведение количественного анализа, как правило, включает в себя построение градуировки, т.е. находждение градуировочной функции экспериментальным путем. Для этого измеряется аналитический сигнал для серии образцов сравнения, в результате получается массив данных: {x_i,y_i}, где x - содержание определяемого компонента, y - аналитический сигнал. На плоскости каждое измерение можно представить точкой:

Градуировочная функция y = f(x) определяется методами регрессионного анализа. Прямо через точки проводить ломаную и считать ее градуировочной функцией нельзя, т.к. измеряемый сигнал содержит погрешность.

Т.о. необходимо:
1) доопределить функцию (между точками)
2) минимизировать погрешность и
3) выбрать вид зависимости.

Вид функции зависимости выбирается исходя из внешней информации (расположения точек на плоскости) и из общих соображений относительно физических и химических законов, связывающих аналитический сигнал с содержанием определяемого компонента (например, построение градуировки в спектрофотометрии опирается на закон Бугера-Ламберта-Бера). Наиболее часто используется линейная зависимость.

Обозначим k - число параметров градуировочной функции, n - число измерений. Мы получаем систему уравнений:

Рассмотрим различные варианты соотношений n и k:

1) n < k - данных недостаточно. Необходимо провести больше измерений или упростить модель - уменьшить число параметров.

2) n = k - у системы единственное точное решение. Однако в этом случае нельзя оценить погрешность измерения

3) n > k - система уравнений несовместна и не имеет точного решения. Существует бесконечное множество приближенных решений, возникает задача аппроксимации.

На практике наиболее распространен 3-й случай. Рассмотрим его более подробно на примере линейного регрессионного анализа (т.е. градуировочная зависимость имеет линейный вид y = ax + b, определяется двумя параметрами a и b, k = 2).

Необходимо найти a и b такие, чтобы погрешность была минимальной.

Один из наиболее распространенных методов нахождения параметров линейной зависимости - метод наименьших квадратов, МНК

Предпосылки МНК:
1) Погрешность аргумента (x) пренебрежимо мала по сравнению с погрешностью y
2) Погрешность y постоянна (не зависит от x) - постулат равноточности (в условиях реального эксперимента погрешность обычно растет с ростом y)
3) Данные подчиняются нормальному закону распределения
4) Данные независимы, коэффициент корреляции r(y_i,y_j) = 0
5) Отклонение градуировочной функции от экспериментальных данных минимально. В рамках метода наименьших квадратов минимизируется величина , где Y_i - величина аналитического сигнала, рассчитанная по уравнению Y = ax + b, y_i - экспериментальная величина аналитического сигнала

С учетом всех предпосылок получаются следующие выражения для a и b:

Источник: Лекции по регрессионному анализу http://chemstat.com.ru/node/12