Артемьева И.Л., Тютюник М.Б. Прототип системы конфлюэнтных продукций для МВС-1000

ПРОТОТИП СИСТЕМЫ КОНФЛЮЭНТНЫХ ПРОДУКЦИЙ ДЛЯ МВС-1000^¹

Институт автоматики и процессов управления ДВО РАН

При появлении многопроцессорных ЭВМ рассматривались различные подходы для получения систем программирования для них.

Во-первых, создавались новые алгоритмические языки для написания параллельных алгоритмов. В таких языках явно присутствуют средства для создания параллельных процессов, для синхронизации их работы и организации их взаимодействия. Примерами таких языков могут служить ответвления языка С.

Во-вторых, были разработаны языки, позволяющие работать параллельно с данными, задаваемыми массивами. Для подобных языков рассматриваются схемы распараллеливания на уровне данных. Ярким примером подобного языка считают HPF (High Performance Fortran).

Наконец, следует сказать о логических языках, которые, в основном, базируются на известном языке Prolog. Среди первых систем, основанных на логическом языке, отметим японскую систему, разработанную в рамках создания компьютеров пятого поколения, которая базируется на высокопродуктивном языке логического параллельного программирования KL1. Хотя KL1 во многом основывается на Prolog и поддерживает режим параллельного вывода, он, тем не менее, ориентирован на конкретную компьютерную архитектуру, и поэтому не реализует в полной мере логику предикатов первого порядка.

Таким же ответвлением, как и KL1, является язык n-Prolog, для которого был разработан свой механизм вывода. Этот механизм позволяет автоматически и незаметно распознавать параллельные части программы Prolog, однако не позволяет полностью распараллелить процесс логического вывода.

Исходя из этого можно сделать вывод о том, что в настоящее время нет языков, которые в полной мере реализуют полностью распараллеленный логический вывод.

Система продукций, описываемая в данной работе, относится к классу конфлюэнтных реляционных продукций [1,2]. В конфлюэнтных системах продукций результат вычислений не зависит от порядка применения правил в процессе логического вывода. Это означает, что все правила являются независимыми друг от друга, т.е. система продукций обладает естественным параллелизмом и не требует никаких дополнительных языковых конструкций для написания параллельных программ.

Разрабатываемая система предназначена для параллельного программирования конфлюэнтных продукций и исполнения сгенерированной программы на многопроцессорной вычислительной машине.

Мультикомпьютер, на котором реализована система параллельного программирования, представляет собой Linux-кластер, состоящий из 16 узлов. Для организации взаимодействия параллельных процессов используется протокол MPI (реализация LAM). Прототип системы построен с использованием подхода «управляющий процесс - зависимый процесс», то есть, применительно к программному средству, объекты и их значения будут храниться в памяти, используемой управляющим процессом, а для передачи данных процессам-обработчикам управляющий процесс снимает копию памяти, где находятся данные. Результаты же обработки объектов, полученные от процесса-обработчика, сравниваются с оригинальными, хранящимися в памяти управляющего процесса, и дополняют их при необходимости.

3. Система декларативных конфлюэнтных продукций

Система декларативных конфлюэнтных продукций моделирует понятия предметной области (ПО) в виде индивидов и отношений. Множество правил логического вывода называется логическим модулем (ЛМ). Объект характеризуется своим именем, классом, определенностью и значением. Имя, класс, определенность задаются при описании объекта. Значение объекта определяется при вводе из файла либо в процессе выполнения модуля [2].

Объекты могут быть двух классов: «индивиды» и «отношения». Объекты класса «индивид» представляют индивиды ПО. Объекты класса «отношение» представляют отношения ПО.

C каждым объектом связан набор атрибутов, определяемый классом объекта. Набор атрибутов определяет область возможных значений и структуру значения объекта. Атрибутом объекта класса «индивид» является сорт объекта: «целый» либо «строковый». Областью возможных значений объекта сорта «целый» является множество целых чисел. Областью возможных значений объекта сорта «строка» являются все строки. Атрибутами объекта класса «отношение» являются число аргументов и сорта аргументов отношения: «целый» либо «строковый».

Элементы множества правил определяют взаимосвязи типа "если-то" между значениями объектов. Элементами множества правил являются правила rule вида

где n Î NAT, Q(X) - формула, U₁(X₁), …, U_n(X_n) - простые формулы, а X, X₁, …, X_n - множества переменных.

Формула Q(X), расположенная в правиле между словами если и то, называется условием правила. Формула U₁(X₁) & … & U_n(X_n), расположенная в правиле после слова то, называется следствием правила. Условие правила является логическим выражением, составленным из соотношений, положительных и отрицательных элементарных формул.

Конъюнктивным множителем следствия правила может быть соотношение, положительная и отрицательная элементарная формула.

Соотношением r является формула, составленная из двух термов, соединенных знаками отношения <, >, =, ¹, £, ³.

Положительная элементарная формула имеет вид nr(vt), где nr - предикатный символ, vt - вектор термов. В качестве предикатного символа может выступать либо имя объекта класса "отношение". Вектор термов составляется из термов t₁, t₂, …, t_nt, где nt Î NAT.

Отрицательная элементарная формула имеет вид ^ nr(vt), где nr - предикатный символ, vt - вектор термов.

Логическим выражением называется формула, построенная по следующим правилам:

а) если l - формула, то ^ l - формула (^ - операция отрицания),

б) если l1, l2 - формулы, то l1 "и" l2 - формула и l1 "или" l2 – формула,

Терм определяет способ вычисления значения. Терм может быть либо элементарным термом, либо выражением [2].

К элементарным термам относятся: строка, число, переменная.

Выражение составляется из элементарных термов tt₁, tt₂, …, tt_n(n Î NAT), соединенных знаками операций +, -, *, / и операций над строками: слияние строк, взятие подстроки, замена подстроки и др. Выражение, не содержащее переменных, будем называть выражением без переменных.

Так как система продукций, рассматриваемая в данной работе, является конфлюэнтной [2], и вычислительная система построена для многопроцессорной ЭВМ, можно использовать параллельные вычисления для обработки правил при всех существующих означиваниях.

В отличие от процесса логического вывод (ПЛВ), реализованного на однопроцессорном компьютере, где каждое правило обрабатывается одно за другим, многопроцессорная машина позволяет построить работу программной системы, реализующей ПЛВ, как набор процессов, выполняемых разными узлами компьютера. Одному из процессов предложена роль диспетчера, управляющего работой по подготовке правил для обработки, в то время как остальные процессы выполняют обработку каждого правила независимо друг от друга. Такое параллельное выполнение вычислений позволяет уменьшить время работы ПЛВ по сравнению с аналогичными вычислениями на однопроцессорной ЭВМ.

Управляющий процесс координирует работу с данными и правилами и организует запуск процессов-обработчиков. Первоначально управляющий процесс производит выборку правил базы правил и формирует множество активных правил. Затем определяется количество свободных процессов-обработчиков, которым и передаются данные, необходимые для обработки каждого правила из множества активных правил. Наконец, данные, полученные от каждого отработавшего процесса, синхронизируются с оригинальными данными. Это значит, что результат выполнения действий, описанных в следствии правила, добавляется к имеющимся данным, а само правило записывается в множество активных правил (МАП), если для него возможно появление новых означиваний (которые обычно появляются в том случае, когда текущее состояние ПЛВ расширяется новыми фактами).

Процесс-обработчик работает в режиме ожидания данных от управляющего процесса и ничего «не знает» о деятельности других процессов. Данные, которые он получает от управляющего процесса, несут информацию только об одном правиле и о тех объектах, которые используются в правиле. После получения данных проверяется условие применимости правила, и формируются действия, выполняемые в результате применения этого правила. Затем все выходные данные пересылаются обратно управляющему процессу.

Формальное описание распараллеленного процесса решения задачи.

П’’ – множество правил, выполненных зависимыми процессами.

q – текущее состояние процесса вывода (множество атомарных формул вида P(h), где P – термин предметной области, h – вектор скалярных констант).

q_-1(p) – множество просмотренных формул в q при всех предыдущих применениях правила p (p Î К, К – база правила), исключая данное.

q_-1_N(p) – новое множество просмотренных формул в q при всех предыдущих применениях правила p, включая данное.

q_N(p) – новое множество просмотренных формул в q при данном применении правила p.

B(P, q) = {P(h) | P(h) Î q} – множество формул вида P(h) из q.

A({P₁, …, P_l}, q, q₁) = (B(P₁, q) ´ … ´ B(P_l, q)) \ (B(P₁, q₁) ´ … ´ B(P_l, q₁)).

X({P₁(t₁), …, P_l(t_l)}) – множество переменных, входящих в формулы P₁(t₁), …, P_l(t_l).

l(x) º L(x, {P₁(t₁), …, P_k(t_k)}) – подстановка, которая формируется следующим образом. Пусть x = (P₁(h₁), …, P_k(h_k)) (P_i(h_i) Î q для i = 1..k), {x₁, …, x_m} = X({P₁(t₁), …, P_k(t_k)}). Пусть (a₁, …, a_m) – единственное решение системы уравнений

тогда положим l_(x) = {x₁/a₁, …, x_m/a_m}. Если система не имеет решения или оно не одно, то положим l = Æ.

ì{[S₁(u₁) | l(x)], …, [S_n(u_n) | l(x)]}, если l(x) ¹ Æ и [F(t) | l(x)] – истина,

СтартПроцесса(p, q) – операция производит запуск находящего в ожидании процесса, который будет выполнять правило p.

ПолучитьРезультат(p, M) – операция получает от отработавшего процесса результат применения правила p.

Опишем с помощью введенных обозначений процесс распараллеленного вывода. Для главного процесса P₀:

Формируем начальное МАП = {p | A(u(p), q, q_-1(p)) ¹ Æ}, где u(p) – множество формул из условия правила p. П’’ = Æ.

- если A(u(p’’), q, q_-1(p’’)) ¹ Æ, то МАП = МАП È {p’ | A(u(p’), q, q_-1(p’)) ¹ Æ};

Зависимый процесс P начинает работу при выполнении команды СтартПроцесса(p, q).

Пусть w₀ = q – начальное состояние процесса P.

w₁ = w₀ È M; M = îþResult(x, {P₁(t₁), …, P_l(t_l)}, {S₁(u₁), …, S_n(u_n)}, F(t)).

Таким образом, на первом шаге управляющий процесс P₀ производит следующие действия:

- имея набор данных v₀, формирует МАП: R₀ = {r₁, r₂, …, r_m};

- eсли R₀ ¹ Æ, то для каждого правила из R₀ выбирает свободный процесс p’ из П₀ и запускает его на наборе данных v’, где v’ – часть данных v_0,необходимая для применения соответствующего правила.

- затем производятся аналогичные действия по запуску свободных процессов для обработки правил из МАП до тех пор, пока не закончатся правила из МАП либо свободные процессы.

На каждом следующем шаге j P₀ проверяет наличие уже отработавших процессов и, в случае их существования, получает результаты работы. Затем p₀ производит обновление данных в связи с появлением новых. Далее управляющий процесс выполняет аналогичные действия для всех оставшихся процессов из множества отработавших процессов.

Далее на шаге j p₀ совершает такие же действия по формированию МАП, запуску процессов, которые были описаны выше.

Справедливо следующее утверждение: при одинаковых начальных данных конечное состояние параллельного процесса логического вывода совпадает с конечным состоянием последовательного процесса логического вывода (то есть результаты работы логического модуля в параллельном и последовательном вариантах одинаковы).

Запишем с помощью введенных обозначений правило вывода, реализованное в системе конфлюэнтных продукций РЕПРО на последовательной ЭВМ:

Формируем начальное МАП = {p | A(u(p), q, q_-1(p)) ¹ Æ}, где u(p) – множество формул из условия правила p.

M = îþResult(x, {P₁(t₁), …, P_m(t_m)}, {S₁(u₁), …, S_n(u_n)}, F(t));

- если A(u(p), q, q_-1(p)) ¹ Æ, то МАП = МАП È {p’ | A(u(p’), q, q_-1(p’)) ¹ Æ};

На основании вышеприведенной модели был реализован прототип системы, который был запущен на МВС-1000. Был проведен набор экспериментов, который показал, что прототип позволяет обрабатывать продукции параллельно, но затрачивает много времени на повторяющиеся вычисления. Для этого при разработке следующей версии прототипа использовали следующие оптимизации.

Оптимизация №1. При построении вычислений для каждого правила системой автоматически создавалась подпрограмма на алгоритмическом языке, где для поиска значений каждого объекта, входящего в условие правила, использовался цикл. Каждый цикл нового объекта является вложенным в цикл предыдущего объекта в условии правила. Таким образом, происходит исключение уже найденных значений из диапазона поиска.

Для того чтобы в этом случае избежать повторных просмотров области значений объектов при повторной активации некоторого правила, с каждым правилом связывается информация о том, какие части области значений были просмотрены ранее, т.е. для каждого правила каждое множество значений объектов делится на две части: «новую» и «старую». Если обозначать просмотр, выполняемый по новой части области значений функции либо отношения с именем fr_i через N(fr_i), по старой – О(fr_i), а по всей области значений – А(fr_i), через «*» - декартово произведение множеств, а через «+» - объединение множеств, то все новые допустимые значения подстановки λ могут быть получены в результате выполнения просмотров следующего множества:

Оптимизация №2. Как отмечалось выше, при работе управляющего процесса важную роль играет формирование множества активных правил, используя которое система распараллеливает обработку правил. Для того, что эффективно производить распараллеливание, множество активных правил формируется в ходе выполнения программы на основе зависимостей по данным. Для этого выполняются следующие шаги.

В первый момент формируется начальное множество активных правил, которое состоит из тех правил, для всех объектов которых существуют данные, вводимые из файла io.txt.

Затем, после обработки очередного правила происходит анализ объектов из следствия правила, для которых появились новые означивания. Если новые кортежи появились, то в множество активных правил заносим те правила, в условия которых входят объекты с новыми кортежами. Таким образом, при обработке правил учитываются связи между правилами, которые описываются информационным графом модуля правил: наличие дуги в графе, ведущей от одного правила к другому означает передачу данных от первого правила к другому. В первом правиле в следствии используется некоторый объект, значение которого вычисляется в процессе выполнения этого правила. Во втором правиле в условии присутствует такой же объект, который используется при вычислении истинности условия применимости правила.

Для получения оценки эффективности работы схемы распараллеливания с добавленными оптимизациями были проведены эксперименты.

В каждом эксперименте измерялось время работы сгенерированных программ для последовательной ЭВМ (Pentium III 800МГц, ОЗУ 256 Мб), а также для кластера на различных наборах данных. Следует отметить, что хотя последовательная машина и имеет такой же процессор, что и отдельный узел кластера, временные показатели на такой машине будут отличаться; и это вызвано различным программным обеспечением, установленным на компьютерах. Данные слова подтверждают приведенные ниже результаты экспериментов.

Целью экспериментов было исследование зависимости времени работы программы от количества входных объектов, от количества правил и количества доступных процессов.

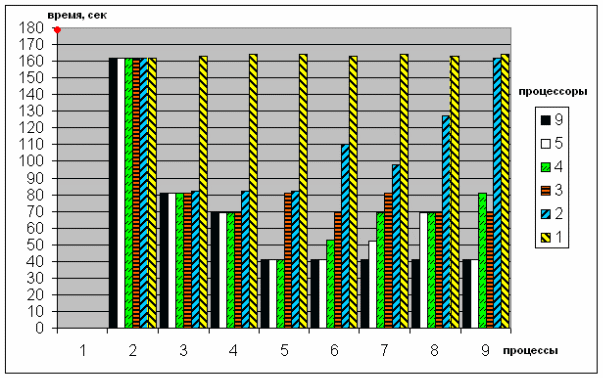
В описании результатов экспериментов приведено среднее время работы программных средств. На всех диаграммах время работы системы, реализованной для последовательной ЭВМ, показано точкой.

Приведем результаты эксперимента, в котором используется 8 правил.

Рис. 2. Диаграмма работы программного средства при обработке 8 правил

Приведем результаты эксперимента, в котором используется 6 правил.

Рис. 3. Диаграмма работы программного средства при обработке 6 правил

Анализ экспериментов. В экспериментах были использованы множества правил, пары которых не зависят друг от друга по данным и могут выполняться параллельно. Результаты экспериментов показали, что обработка данных правил на кластере дает выигрыш во времени по сравнению с вычислениями на однопроцессорной машине.

На основании экспериментальных данных можно высказать предположение, что если количество выделяемых для работы процессоров больше, чем количество процессов, то время работы программы не изменится по сравнению со временем работы программы при числе процессоров, равном числу процессов. Однако, если увеличивать количество процессов при неизменном количестве процессоров, время исполнения начинает увеличиваться. Особенно заметна данная тенденция при количестве процессоров, равном 2. При большем количестве процессов время увеличивается из-за того, что MPI пытается распределить обработку правил по свободным процессам, однако процессоры в это же время уже заняты обработкой других правил. Тем самым, процессорное время начинает распределяться между процессами и общая скорость вычислений понижается.

В одном из экспериментов использованы правила, данные в которых являются зависимыми, то есть каждое правило не может дать результатов до тех пор, пока не выполнятся другие правила. В таком случае обработка правил на параллельной машине не дает выигрыша, так как параллельной обработки правил достичь нельзя.

Следует отметить, что наиболее эффективной работа программы будет в том случае, когда задача, которую необходимо решить, описана в виде правил, имеющих мало зависимых друг от друга данных и обладающих способностью быть исполненными параллельно. При этом оптимальное количество процессов и процессоров следует задавать равным числу правил, способных выполняться параллельно.

В работе была рассмотрена система параллельного программирования для конфлюэнтных реляционных продукций. В ней результат вычислений не зависит от порядка применения правил в процессе логического вывода. Описанная схема распараллеливания для данной системы использует при вычислениях тот факт, что все правила являются независимыми друг от друга, т.е. система продукций обладает естественным параллелизмом. Оптимизация вычислений позволяет добиться лучшего времени выполнения системы.

Схема распараллеливания, рассмотренная выше, не является единственной для системы конфлюэнтных продукций. Одной из альтернативных схем организации процесса логического вывода является схема, в которой учитываются связи между правилами по передаче данных; эти связи отражаются в графе передачи данных. Если при учете связей между правилами может быть построена последовательность правил, тогда при организации работы на параллельной системе распараллеливается процесс выполнения одного правила. Если же в графе существует несколько ветвей, то распараллеливание состоит в параллельном выполнении веток. В дальнейшей работе предполагается исследовать все возможные схемы распараллеливания, получить оценки времени выполнения для каждой из схем и выбрать более оптимальную схему для реализации системы конфлюэнтных продукций на многопроцессорной ЭВМ.

1 Работа выполнена в рамках программы №17 фундаментальных исследований Президиума РАН на 2004 год № 10002-251/П-17/026-387/190504-301.