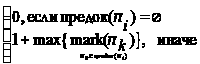УДК 004.8+004.032.24

И.Л. Артемьева, М.Б. Тютюнник

Институт автоматики и процессов управления ДВО РАН, г. Владивосток, Россия

artemeva@iacp.dvo.ru, michaelhuman@gmail.com

Методы управления распараллеливанием вычислений в системе конфлюэнтных продукций^*

Данная работа описывает исследования, целью которых является разработка системы параллельного программирования на основе декларативных продукций. В ней рассматривается набор схем распараллеливания вычислений логической программы и методы управления ими.

Введение

При разработке прикладных программ для многопроцессорных вычислительных комплексов (МВК) (в частности, для кластерных систем) используются либо специальные языки, имеющие средства задания параллельных процессов и организации их взаимодействия, либо традиционные языки программирования. Одним из классов языков, которые могут использоваться при создании прикладных программ для МВК, являются продукционные языки.

В системах конфлюэнтных продукций (КП) результат вычислений не зависит от порядка применения правил в процессе логического вывода (ЛВ). Это означает, что все правила являются независимыми друг от друга, т.е. язык для записи КП не требует никаких дополнительных языковых конструкций для написания параллельных программ. Задачу распределения вычислений по процессам решает языковой процессор продукционного языка.

При формировании объектной программы языковой процессор анализирует свойства исходной программы, множество ограничений, налагаемых вычислительной средой, а также свойства входных данных, определяемых пользователем, и выбирает наиболее применимую схему распараллеливания вычислений. Целью данной работы является описание условий, влияющих на выбор схемы, и методов управления схемами.

Группы схем распараллеливания

Программа, записанная на продукционном языке, имеет следующие компоненты: описание переменных, значения которых задают входные и выходные данные программы, продукционные правила, описывающие метод решения задачи. Программа может состоять из одного или нескольких модулей. Каждый из модулей решает свою подзадачу. Управление между модулями описывается средствами алгоритмического языка.

Языковой процессор представляет собой компилятор, преобразующий текст на продукционном языке в объектную программу на алгоритмическом языке высокого уровня. Объектная программа реализует процесс логического вывода, задаваемый продукционными правилами, и содержит обращения к модулям среды поддержки периода выполнения.

До генерации объектной программы языковой процессор строит информационный граф программы и анализирует его свойства. Информационным графом (ИГ) программы будем называть ориентированный цикличный граф, вершинами которого являются модули программы, а дуги обозначают информационные связи между модулями, то есть дуги связывают те модули, которые обмениваются между собой данными.

В свою очередь каждый модуль программы также описывается с помощью ориентированного цикличного графа.

Введем необходимые обозначения.

ПР = áМñ, ПР – логическая программа, М – множество модулей программы, М = <П>, П = {p₁, …, p_p}, П – множество правил программы.

p_i = áOñ, O = {o₁, …, o_o}, где O – множество объектов правила p_i.

Определим множество IF(p_i) = {o₁’, …, o_a’} – множество предикатных и функциональных символов условия правила p_i, множество THEN(p_i) = {o₁’’, …, o_b’’} – множество предикатных и функциональных символов следствия правила p_i, такие, что IF(p_i) È THEN(p_i) = O.

Правило p_j будем называть зависимым от правила p_i, если THEN(p_i)ÇIF(p_j)¹ Æ.

K(o_i) = {k₁, …, k_k}, где K(o_i) – множество кортежей объекта o_i.

GМ = (П, ED) – ориентированный цикличный граф программы, где П – множество вершин графа, причем каждая вершина соответствует правилу p программы, ED = {(p_i, p_j): THEN(p_i) Ç IF(p_j) ¹ Æ, i ¹ j} – множество дуг графа.

Информационным графом модуля (ИГМ) программы будем называть ориентированный цикличный граф GМ.

Таким образом, получается двухуровневый граф, верхний уровень которого представляет собой граф программы, состоящей из модулей, а нижний уровень описывает графы каждого модуля, состоящего из правил.

Введем следующие обозначения.

E(GМ) = {e₁, …, e_e}, e_i – предполагаемое время вычисления правила p_i, равно весу вершины p_i графа GМ.

ВПД(p_i, p_j) = d_ij * ВПДУ, где ВПДУ – время передачи данных от процесса, обрабатывающего правило p_i, процессу, обрабатывающему правило p_j.

max(e_i) = ВОК * m(К₁) * m(К₂) * … * m(К_k), k = m(O_i), где ВОК – время обработки одного кортежа, – максимальное время обработки правила p_i, равно времени выполнения полного перебора всех кортежей правила.

D(GМ) = {(d_ij): i ¹ j}, где d_ij – объем (количество кортежей) передаваемых данных от процесса, обрабатывающего правило p_i, процессу, обрабатывающему правило p_j, то есть вес дуги, соединяющей вершины p_i и p_j графа GМ.

max(time(GМ)) = max(E(GМ)) + time(D(GМ) * ВПДУ)), где time(GМ) – время вычисления всех правил П, описанных в GМ, time(D(GПР) * ВПДУ)), – время передачи всех данных между процессами, которые обрабатывали правила П.

Mark(GМ) = {(mark(p_i))} – множество меток для вершин графа GМ,
где mark(p_i) = .

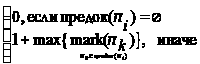Пар1(p_i) = {p_i, p_i1, …, p_iz}: mark(p_i) = mark(p_i1) = mark(p_i2) = … = mark(p_iz) – множество правил, которые можно начать выполнять параллельно с правилом p_i и друг с другом.

ПарМ(p_i) = {p_i, p_i1, …, p_iz}: "mark’Î{mark(p_i1), …, mark(p_iz)) mark(p_i) £ mark’ < < max(mark(потомок(p_i))) – множество правил, которые можно выполнять параллельно с правилом p_i (но не обязательно параллельно друг с другом).

Множество ПарМ(p_i) состоит из объединения Пар1(p_j) для всех p_jÎПарМ(p_i). При этом максимально возможное количество процессов, работающих параллельно с правилом p_i, равно максимальному количеству элементов в любом из множеств Пар1(p_j) плюс один процесс, выделяемый для p_i. Следовательно, число требуемых программе процессов не превышает максимального количества элементов из ПарМ(p_i) для всех правил, входящих в программу. Это условие действует лишь в том случае, когда процесс обрабатывает целое правило (а не кортежи по отдельности, например).

Множеством активных правил (МАП) будем называть набор правил, которые система может обработать на текущем шаге процесса логического вывода. Правила, входящие в МАП, имеют как минимум один кортеж для каждого объекта (отношения или функции), входящего в условие правила, и могут выполняться параллельно и независимо друг от друга. На каждом следующем шаге процесса логического вывода правило попадает в МАП в том случае, если появился новый кортеж для любого из объектов, входящих в условие правила.

Далее рассмотрим группы примеров схем распараллеливания процесса логического вывода.

Распараллеливания вычислений с использованием множества активных правил

Введем обозначения. Пусть П’ – множество правил, выполняемых зависимыми процессами; П’’ – множество правил, выполненных зависимыми процессами; p – правило логической программы; СтартПроцесса(p) – набор действий по запуску процесса для вычисления правила p; ПолучитьРезультат(p, M) – набор действий по приему вычисленных данных М правила p из отработавшего процесса; Синхронизировать (M) – набор действий по синхронизации данных, полученных из отработавшего процесса, с данными, хранящимися в управляющем процессе; Вычислить (p, М) – набор действий по вычислению правила p, то есть по поиску новых значений М объектов, входящих в следствие правила.

Опишем с помощью введенных обозначений процесс распараллеленного логического вывода.

Начало главного процесса; Сформировать МАП; П’ = Æ; П’’ = Æ;

Пока МАП ¹ Æ выполнить: выбрать p Î МАП; МАП = МАП \ {p};

СтартПроцесса(p); П’ = П’ È {p}; Конец_цикла;

Пока Ø(МАП = Æ и П’ = Æ) выполнить:

Если П’’ ¹ Æ, то ПолучитьРезультат(p’’, M); Синхронизировать (M); Сформировать МАП; П’’ = П’’ \ {p’’}; конец_условия;

Пока МАП ¹ Æ выполнить: выбрать p Î МАП; СтартПроцесса(p);

МАП = МАП \ {p}; П’ = П’ È {p}; конец_цикла;

конец_цикла; Конец главного процесса.

Зависимый процесс начинает обрабатывать правило при выполнении команды СтартПроцесса(p).

Начало зависимого процесса;

Вычислить(p, М); П’’ = П’’ È {p}; П’ = П’ \ {p};

Конец зависимого процесса.

Прокомментируем приведенные алгоритмы. Вначале управляющим процессом формируется МАП. Оно содержит те правила, для объектов которых в исходных данных заданы значения и которые не зависят по данным от других правил. Далее в цикле поочередно каждому правилу из МАП сопоставляется зависимый процесс. Управляющий процесс ждет результата выполнения хотя бы одного из зависимых процессов, после чего происходит обновление МАП: это множество пополняется теми правилами, для объектов которых появляются новые означивания. В случае пополнения МАП новыми правилами происходит передача этих правил свободным процессам для вычислений. При формировании МАП очередь отработавших процессов увеличивается, однако они не могут получить новых данных для обработки до тех пор, пока не передадут результаты в управляющий процесс. Программа завершает работу тогда, когда не останется зависимых процессов, обрабатывающих правила, и МАП будет пустым. В данной схеме дополнительные расходы связаны с организацией поддержки МАП. Схема применена в прототипе системы [1], ее исследования приведены в [2].

Вычисление правил с использованием информационного графа

При описании схемы будем предполагать, что количество доступных рабочих процессов равно максимальному количеству правил, которые можно вычислить параллельно.

Приведем алгоритм, который назначает каждому правилу соответствующий процесс. Построим вспомогательную таблицу, число строк которой равно трем, а число столбцов равно количеству правил (и количеству меток). В первой строке размещаются метки ИГ, упорядоченные по возрастанию слева направо, во второй строке – номера правил, соответствующие меткам, в третьей будем записывать номера процессов, которые назначим для выполнения правил.

Алгоритм № 1 назначения номеров процессов.

1. Берем из строки таблицы, содержащей множество меток, первую слева метку и назначаем ей первый доступный процесс, то есть производим запись в ячейку строки таблицы, содержащей записи о номерах процессов.

2. Берем следующую метку в ячейке справа от метки, выбранной в пункте 1.
   – если выбранная метка равна стоящей в ячейке слева, то назначаем следующий доступный процесс. Если все доступные процессы уже назначены, то тогда начинаем назначать процессы заново, начиная с первого процесса.
   – если эта метка больше стоящей слева, то назначаем тот же самый процесс, который назначен метке слева.

3. Выполняем шаг 2 до тех пор, пока не назначим процессы всем правилам.

В течение работы каждый процесс выполняет подпрограммы, соответствующие отдельному правилу и построенные на этапе трансляции [3]. Так как процессы работают каждый со своим участком памяти (ввиду специфики кластера), им необходимо пересылать друг другу результирующие данные и данные синхронизации.

Каждый процесс производит одинаковые действия по обработке правил. Это получение необходимых данных для каждого правила от управляющего или рабочих процессов, синхронизация полученных данных с уже имеющимися в наличии, вычисление правила и отправка результата работы зависимым правилам и процессам. При этом роль управляющего процесса сводится к начальной инициализации данных, запуску всех рабочих процессов и получению необходимых результатов вычисления правил.

Алгоритм № 2 работы процесса:

1. Принять входные данные для правил p₁, p₂, …, p_n от управляющего процесса.

2. Для каждого правила p₁, p₂, …, p_n выполнить шаги 3 – 10.

3. Если правило p_i зависит от правила, находящегося в этом процессе, то принять входные данные для правила p_i от правила, от которого зависит p_i.

4. Если правило p_i зависит от правила, находящегося в этом процессе, то синхро­низировать входные данные для правила p_i с входными данными от правила, от которого зависит p_i.

5. Если правило p_i зависит от правила, находящегося в другом процессе, то принять входные данные для правила p_i от процесса, обрабатывающего правило, от которого зависит p_i.

6. Если правило p_i зависит от правила, находящегося в другом процессе, то синхро­низировать данные для правила p_i с входными данными от процесса, обрабатывающего правило, от которого зависит p_i.

7. Начать обработку правила p_i.

8. Если от правила p_i зависит другое правило в этом процессе, то переслать результаты работы зависимому правилу.

9. Если от правила p_i зависит правило в другом процессе, то переслать результаты работы зависимому процессу.

10. Перейти на шаг 2.

11. Переслать необходимые результаты работы правил p₁, p₂, …, p_n в управляющий процесс.

Передача кортежей при неполном вычислении правила

В предыдущей схеме было жестко задано, что зависимое правило не может быть вычислено до тех пор, пока не вычислено правило, от которого оно зависит. В данной схеме такого ограничения нет – очередное правило ждет появления хотя бы одного кортежа – результата выполнения правила, от которого зависит, а не завершения работы всех правил-предков. Если каждый новый кортеж появляется в начале выполнения правил, то можно получить ситуацию, когда все правила обрабатываются параллельно вне зависимости от того, как они информационно связаны.

Каждая подпрограмма, описывающая обработку правила, будет состоять из трех частей. Первая часть отвечает за прием новых кортежей, вторая – за выполнение правила, третья – за передачу порожденных кортежей другим правилам.

Опишем более подробно процесс выполнения правила. Если перед выполнением правила все объекты из условия имеют значения (такое правило может быть корневым или входить в состав петли), то начинаем вычисление новых кортежей, являющихся результатом обработки правила. Как только в процессе вычисления появляется новый кортеж, отсылаем его в соответствующий процесс, обрабатывающий зависимое от данного кортежа правило. Если правило не корневое, то есть имеющее правило-предка, то после блока, использующего начальные данные для вычисления результата, выполняется прием нового кортежа значений от правил-предков. Когда приходит кортеж значений, эти данные обновляются с уже полученными данным процессом, и запускается вновь блок вычисления новых кортежей, являющихся результатом обработки правила. Каждый вновь полученный кортеж также отправляется в зависимые процессы. После вычисления кортежей вновь переходим к приему новых кортежей от правил-предков. В случае приема информации о завершении работы всех правил-предков, работу данной подпрограммы можно завершить (при этом необходимо учесть, входит ли правило, обрабатываемое подпрограммой, в состав петли).

Описанный выше процесс требует следующего: каждая подпрограмма по обработке отдельного правила должна быть запущена одновременно в отдельном процессе.

Если правил и соответствующих подпрограмм n штук, то тогда необходимо запустить n штук процессов по обработке правил. Однако запуск, например, 10 процессов на 2 физических процессорах можно считать неудачным решением, так как следует ожидать многочисленных задержек по системному обслуживанию данных процессов (если будем оперировать сотнями правил, то падение производи­тельности очевидно). В данном случае необходимо ввести регулирующую функцию, назначив ее управляющему процессу.

Функция будет состоять в том, чтобы управляющий процесс раздал правила (в по­рядке очередности, определяемой информационным графом) всем свободным рабочим процессам. Если количество правил больше количества доступных процессов, то в дан­ной ситуации все вновь вычисленные кортежи, которые необходимо переслать в еще не запущенные на обработку правила, будут пересылаться в управляющий процесс. Для этого заводится множество объектов без значений и эти объекты заполняются кортежами, присланными из работающих процессов. При этом каждый объект хранит номера правил, в которые необходимо будет переслать кортежи. Как только освобождается какой-то процесс и запускается новое правило, то все кортежи объекта, входящего в условие та­кого правила, пересылаются из управляющего процесса в зависимый, обрабатывающий новое правило. Если при этом правила-предки пересылали кортежи в управляющий про­цесс из-за того, что правило-потомок не было запущено, то таким правилам пересылается номер процесса, который начал обрабатывать зависимое правило. Тем самым происходит переключение пересылки кортежей не в управляющий процесс, а в зависимый.

Порядок выполнения правил, которого придерживается управляющий процесс, определяется на основе множества меток mark(GПР).

Из вышесказанного видно, что эффективность вычислений растет с увеличением количества доступных рабочих процессов, выделяемых без ущерба производительности (на системном уровне). Идеальным случаем является тот, в котором количество всех правил совпадает с количеством выделенных процессов.

Таким образом, видно, что когда работаем с кортежами в отдельных правилах, пересылая и принимая их в процессе вычисления правил, то более эффективно распоряжаемся предоставленной параллельностью. Такая эффективность работы не возможна в случае, когда работаем полностью с отдельным правилом.

Далее приведем алгоритмы работы управляющего и зависимых процессов с использованием схемы, распараллеливающей вычисления с помощью пересылки кортежей. Для этого введем условные обозначения.

N – количество правил.

N_f – количество свободных процессов.

М = {(1,0), (2,i), …, (N,i^M)} – множество номеров правил.

M_w – множество пар «(номер правила, номер процесса)», находящихся в обработке.

m(M_w) – количество элементов множества M_w.

P_f = {1, 2, …, N_f} – множество номеров свободных процессов.

P_w – множество номеров работающих процессов.

П_s(Q) – множество номеров правил, зависимых от объекта Q.

data(p) – данные для правила p: объекты и кортежи значений этих объектов, входящих в условие правила; данные о номере правила, зависящего от конкретного объекта (П_s(Q)).

G(M_w, i) – множество, сформированное из i-х элементов, входящих в состав пар, из которых состоит множество M_w. Например, M_w = {(1,2),(4,5)}, G(M, 1) = {1, 4}.

g(M_w, i, j) – функция возвращает значение второго, не-j-го элемента той пары из множества пар M_w, j-й элемент которой равен i. Например, M_w = {(1,2),(4,5)}, g(M, 4, 1) = 5.

ВычислитьКортеж(O) – возвращает каждый раз очередной вычисленный кортеж объекта O, входящего в следствие правила.

ОтправитьКортеж(q(O), p, r) – отправить кортеж q объекта O в процесс p, в котором обрабатывается правило, зависимое по O, причем r Î {0, 1}, r = 1 – операция ОтправитьКортеж() передает некоторое значение объекта, r = 0 – операция ОтправитьКортеж() передает пустое значение объекта и сообщает процессу-приемнику, что больше значений передаваться не будет, r = –1 – операция ОтправитьКортеж() передает пустое значение объекта процессу-приемнику и сообщает ему, что подпрограмма закончила вычисление. Если номер процесса равен 0, то это значит, что кортеж будет передаваться управляющему процессу.

ПолучитьКортеж(q(O), r, p) – получить кортеж q объекта O, переданный процессом p. Если при запуске операции ПолучитьКортеж() будет найдено хоть одно передаваемое значение объекта, то операция возвращает значение “true”, если ни одно из передаваемых значений объектов найдено не будет, операция возвратит значение “false”. r Î {0, 1}, причем если r = 1, то принятое значение объекта можно использовать дальше, если r = 0, то это значит, что правило-предок, обрабатываемое процессом p, больше не будет передавать данные и завершило работу.

Синхронизировать(q(O)) – синхронизировать кортеж, полученный от правила-предка с кортежами объекта О, входящего в условие правила.

СинхронизироватьУ(q(O), r) – синхронизировать кортеж, полученный от правила-предка с кортежами объекта О, входящего в условие правила.

СтартПроцесса(p, p, D); – номер правила, номер процесса, данные об объектах.

R_p – количество объектов, входящих в следствие правил-предков для правила p, от которых будут передаваться значения этих объектов.

ПолучитьМетки(M_w, R) – получить из управляющего процесса: M_w – множество пар меток правил и процессов, которые обрабатывают правила, R – число объектов, кортежи которых будут передаваться в правило.

ОтправитьМетки(M_w, i, R) – отправить из управляющего процесса: M_w – множество пар меток правил и процессов, которые обрабатывают правила; i – номер процесса, куда отправлять, R – число объектов, кортежи которых будут передаваться в правило.

ОпределитьФлаги(p) – функция возвращает количество объектов, для которых будут переданы кортежи в правило p из управляющего процесса.

Алгоритм работы управляющего процесса будет таким:

Начало;

M_w = Æ; P_f = {1, 2, …, N_f}; P_w = Æ; k = m(M_w);

Если N_f < k, то k = N_f;

В цикле от 1 до k выполнить:

выбрать p из (p, i) Î М; М = М \ {(p, i)};

выбрать p Î P_f; N_f = N_f – 1; P_f = P_f \ {p}; P_w = P_w È {p};

M_w = M_w È {(p, p)}; D = (data(p), R_p); СтартПроцесса(p, p, D);

конец_цикла;

В цикле по всем элементам i Î P_w выполнить: ОтправитьМетки(M_w, i, 0);

пока Ø(M = Æ и P_w = Æ) выполнить:

// Принимает кортежи

flag = 1;

Пока flag ¹ 0 выполнить:

y = ПолучитьКортеж(q(O), r, p);

Если y = “true” и r > –1, то

// Процесс p закончил передавать кортежи

СинхронизироватьУ(q(O), r);

иначе если y = “true” и r = –1, то

// Процесс p закончил работу

N_f = N_f + 1; P_w = P_w \ {p}; P_f = P_f È {p}; M_w = M_w \ {(g(M_w,p,2),p)};

иначе flag = 0;

конец_условия;

конец_цикла;

// Запуск новых процессов по обработке новых правил

k = m(M_w);

Если N_f < k, то k = N_f;

В цикле от 1 до к выполнить:

выбрать p из (p,i) Î М; М = М \ {(p,i)};

выбрать p Î P_f;

N_f = N_f – 1; P_f = P_f \ {p}; P_w = P_w È {p}; M_w = M_w È {(p,p)};

D = (data(p), R_p); СтартПроцесса(p, p, D);

конец_цикла;

В цикле по всем элементам i Î P_w выполнить:

R = ОпределитьФлаги(i);

ОтправитьМетки(M_w, i, R);

конец_цикла;

// Пересылка кортежей процессам

В цикле по всем элементам O Î {O₁,…, O_t} выполнить:

В цикле по всем элементам i Î П_s(О) выполнить:

Если i Î G(M_w,1), то

// Если зависимое правило обрабатывается

ОтправитьКортеж(q(O), g(M_w, i), 1);

конец_условия;

конец_цикла;

конец_цикла;

конец_цикла;

Конец.

Ниже приведем алгоритм работы зависимого процесса:

Начало;

M_w = Æ; fflags = R_p;

МЕТКА:

В цикле по значениям О₁

В цикле по значениям О₂

…

В цикле по значениям О_k

q(Q₁) = ВычислитьКортеж(Q₁);

…

q(Q_x) = ВычислитьКортеж(Q_x);

X = ПолучитьМетки(M_w’, R);

Если X = “true”, то

// Если появились новые зависимые правила,

// то надо передать информацию об этом нулевому процессу

В цикле по всем элементам Q Î {Q₁, …, Q_x} выполнить:

В цикле по всем элементам i Î П_s(Q) выполнить:

Если i Ï G(M_w, 1) и i Î G(M_w’, 1), то

ОтправитьКортеж(Æ, 0, 0);

конец_условия;

конец_цикла;

конец_цикла;

M_w = M_w’;

fflags = fflags + R;

конец_условия;

В цикле по всем элементам Q Î {Q₁, …, Q_x} выполнить:

В цикле по всем элементам i Î П_s(Q) выполнить:

Если i Î G(M_w, 1), то

ОтправитьКортеж(q(Q), g(M_w, i), 1);

иначе

ОтправитьКортеж(q(Q), 0, 1);

конец_условия;

конец_цикла;

конец_условия;

конец_цикла;

…

конец_цикла;

конец_цикла;

flag = 1;

Пока flag ¹ 0 выполнить:

y = ПолучитьКортеж(q(O), r, p);

Если y = “true” и r = 0, то fflags = fflags – 1;

иначе если y = “true” и r = 1, то Синхронизировать(q(O));

иначе flag = 0;

конец_условия;

конец_цикла;

Если fflags > 0, то

Goto МЕТКА;

иначе

// Отправляем информацию о завершении

В цикле по всем элементам Q Î {Q₁, …, Q_x} выполнить:

В цикле по всем элементам i Î П_s(Q) выполнить:

Если i Î G(M_w, 1), то

ОтправитьКортеж(Æ, g(M_w, i), 0);

конец_условия;

ОтправитьКортеж(Æ, 0, –1);

конец_цикла;

конец_цикла;

конец_условия;

Конец.

Применяя данную схему, можем запускать в параллельном режиме процесс, кото­рый будет обрабатывать зависящее по данным правило не тогда, когда правило-предок уже выполнилось, а когда от него станут поступать означивания для объектов, найденные в ходе вычислений. Таким образом, если зависимость по данным позволяет, можно запускать все правила в параллельном режиме по мере появления соответствующих означиваний. Отсюда следует, что время выполнения всех правил может быть меньше времени выполнения правил с использованием первой схемы.

Относительным недостатком второй схемы можно считать требовательность к количеству свободных процессов. В случае, когда количество правил значительно больше количества процессов, следует использовать механизм, который может управлять использованием первой схемы при вычислении всех правил программы и применять вторую схему для правил, для которых в ИГ возникают сложные в вычислительном плане участки.

Условия, влияющие на выбор схем

Как видно из приведенных обозначений, свойствами информационного графа являются количество его вершин, количество ветвей графа, которые можно обрабатывать в параллельном режиме и т.д.

Для выбора той или иной схемы распараллеливания процесса логического вывода необходимо знать не только свойства графа, но и архитектурные и системные ограничения, налагаемые вычислительной средой.

Ограничения могут быть следующими.

1. Количество доступных системных процессов. Если количество процессов больше или равно количеству правил в программе, то данный случай удобен для вычислений, так как можно заранее каждому процессу назначить на обработку конкретное правило. Если количество процессов меньше количества правил, то правила процессам назначаются динамически.

2. Время выполнения отдельного правила. При вычислении отдельного правила может возникнуть ситуация, когда это правило будет обрабатываться во много раз дольше, чем любое другое правило логической программы. В этом случае может возникнуть длительный простой системы в ожидании завершения вычислений данного правила. Одним из выходов является пересылка промежуточных результатов вычисления правила в другие процессы, обрабатывающие зависимые правила. Также следует добавить, что имеется возможность оценить максимальное время вычисления каждого правила до запуска системы. Такие оценки помогут заранее определить «тяжелые правила» и применить соответствующие схемы.

Для выбора схемы из третьей группы языковой процессор во время компиляции должен иметь информацию о свойствах входных данных программы. Эта информация может задавать максимальный размер данных для каждого используемого правилом объекта. Знание этой информации дает возможность вычислить условное время выполнения каждого правила и его фрагментов. При применении схемы третьей группы процессам сопоставляется код, соответствующий вычислениям, задаваемым фрагментами правил.

Литература

1. Артемьева И.Л., Тютюнник М.Б. Схемы распараллеливания вычислений для системы конфлюентных продукций // Информатика и системы управления. – 2005. – № 2. – С. 102-112.

2. Артемьева И.Л., Тютюнник М.Б. Методы распараллеливания вычислений для системы параллельного программирования на основе декларативных продукций // Труды II Междунар. конф. «Параллельные вычисления и задачи управления». – Москва: ИПУ РАН. – 2004. – С. 727-737.

3. Артемьева И.Л., Тютюнник М.Б. Прототип системы конфлюэнтных продукций для МВС-1000 // Информатика и системы управления. – 2004. – № 2 (8). – С. 133-144.

4. Матвеева Т.О., Чернойван К.Г. Экспериментальное исследование оптимизаций декларативных продукций: Препр. / Владивосток: ИАПУ ДВО РАН, 1994.