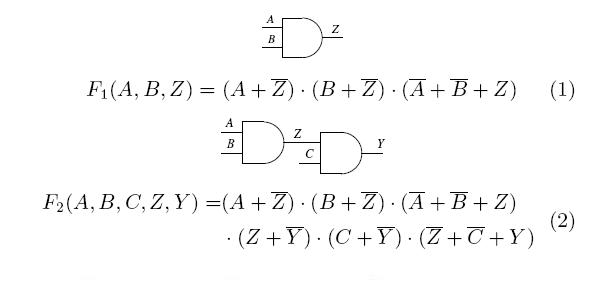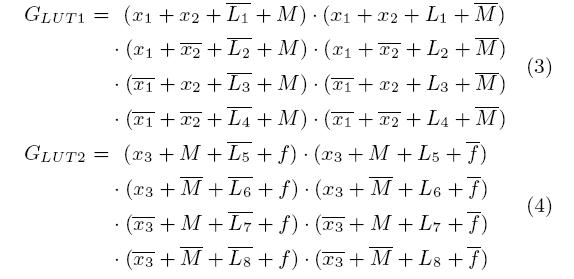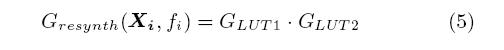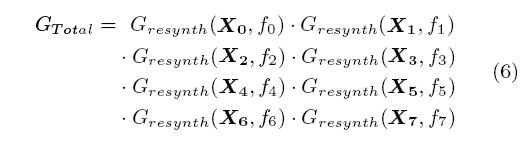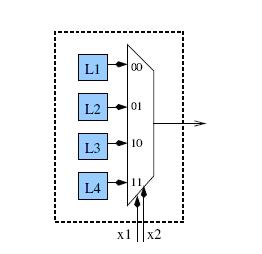
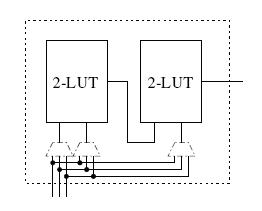
Технологическое картографирование FPGA: Исследование оптимальности.

Первоисточник

Резюме

Эта статья призвана определить оптимальность алгоритмов технического картографирования FPGA технологий. Мы разрабатываем алгоритм, основанный на технологии SAT (Boolean satis f ability), который позволяет преобразовать маленькую подсхему с минимально возможным использованием числа генераторов логических функций ( LUTs - Look Up Table ). Мы многократно многократно применяли эту технологию к маленьким частям схем, которые уже были преобразованы при помощи лучших алгоритмов картографирования FPGA .

Во большинстве случаях, оптимальное преобразование(картографирование) подсхем позволяло использовать меньшее количество LUT , по сравнению с исходным алгоритмом преобразования. Мы показываем, что для некоторых схем суммарное усовершенствование занимаемого пространства может достигать 67%.

Введение.

FPGAs (программируемая вентильная матрица) – реконфигурируемые интегральные схемы, характеризующиеся множеством программируемых логических блоков, окруженных конфигури­руемыми межсоединениями. Самые современные устройства FPGA содержат программируемые логические блоки, основанные на K- input просмотровых таблицах ( K - LUT ), каждый K - LUT содержит 2^ K конфигурируемых бит, с помощью которых реализуется любая K - input функция.

Рисунок 1 иллюстрирует общую структуру 2-х входового LUT .

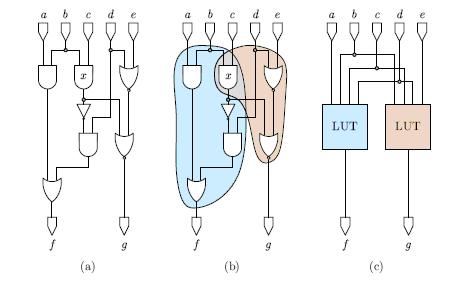
Число LUT -ов необходимое для реализации предоставленной схемы определяет размер и стоимость FPGA - based реализации. Поэтому одна из самых главных фаз автоматизированного проектирования FPGA – картографирование, которое переносит описание логической схемы на множество LUT элементов архитектуры FPGA .

Цель технологии картографирования - сократить используемое пространство, задержку, или комбинацию того и другого в сети программируемых логических блоков. В этой работе оцениваются современные технологии алгоритмов нанесения на карту с точки зрения оптимизации занимаемого пространства. Картографирование по временным параметрам в этой статье рассматриваться не будет.

Процесс технологического картографирования связывают с задачей о покрытии. Например, рассмотрим процесс составление схемы в LUT (Рисунок 2). Рисунок 2 a иллюстрирует начальную сеть на вентильном уровне, рисунок 2 b иллюстрирует возможное покрытие начальной сети с использованием 4- LUTs , и рисунок 2 c иллюстрирует уже покрытую сеть LUT . В предоставленной схеме, вентиль с меткой x покрывается обоими LUT , т.е. дублируется. Удивительно, но дублирование вентилей часто необходимо для минимизации области сетей LUT

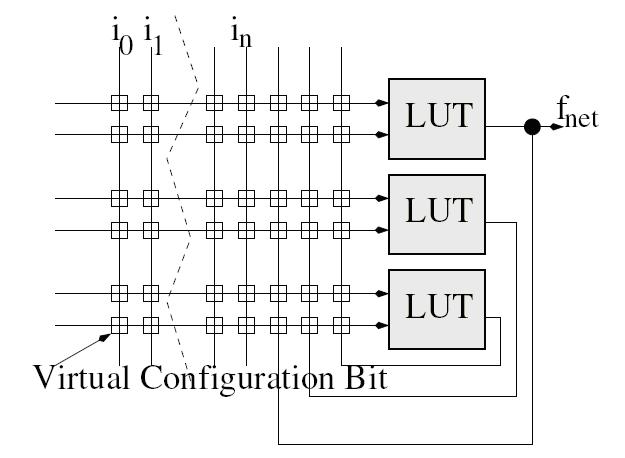
Фундаментальный вопрос, который мы спрашиваем в этой статье, это: на сколько может быть уменьшена область, для полученной сети LUT , созданной при помощи алгоритма технологического картографирования? Рассмотрим произвольную функцию f ( i 0; i 1; : : : ; in ).

Предположим, что мы стремимся определить, можно ли уменьшить область при использовании трех или меньше двухвходовых LUT . Эта задача может быть решена при рассмотрении конфигурируемой виртуальной сети (Con fi gurable Virtual Network CVN) (рисунок 3).

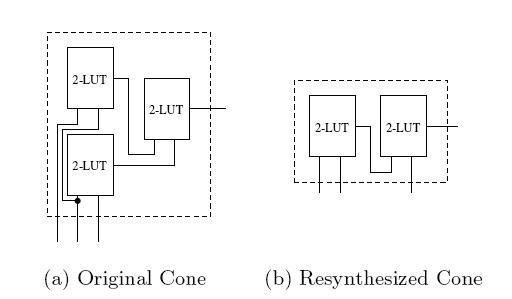
CVN состоит из входных линий соединенных с переменными i 0… in и трех 2-х входовых LUT . Поперечная связь позволяет входам LUT выбрать любую из входных или выходных линий другого LUT . Каждый “переключатель” на перекладине - конфигурируется виртуальным битом конфигурации. «0» - указывает что контакт разъединен, а «1» - связь присутствует. Очевидно, что можно перечислить каждую возможную схемную конфигурацию включающую в себя три 2-х входовых LUT манипулируя виртуальными битами конфигурации для поперечной связи также как и таблица истинности конфигураций битов каждого из 2-х входовых LUTs . Фактически, мы можем выразить выход fnet , как логическое выражение, включающее переменные i 0… in , виртуальные биты конфигурации V 1… Vm и конфигурационные биты таблицы истинности L 1… Lo . Получив эту формулу, мы задаем вопрос: существуют ли значения V 1… Vm и L 1… Lo такие, что функция fnet ( i 0; i 1; in ; V 1… Vm ; L 1… Lo ) бубет идентична функции f ( i 0; i 1; in ) для всех значений i 0… in ? Ответ на этот вопрос позволит дать технология SAT :

Получив логическое выражение в КНФ ( CNF ), где выражение состоит из произведения выражений и каждое выражение состоит из суммы переменных, ищем такое значение переменных таким образом, чтобы каждая переменная превращала выражение в “ 1” .

Сложность разрешения этой задачи экспоненциально возрастает с повышением числа переменных n виртуальной сети. Однако, мы показываем, что этот способ можно использовать только для повторного синтеза маленьких схем.

Получив оптимальный метод повторного синтеза для маленьких подсхем, мы без усилий многократно применяем эту технику к маленьким частям больших схем методом скользящего окна до тех пор, пока дальнейшее усовершенствование не может быть достигнуто.

Этот подход не гарантирует оптимальность при использовании больших схем, но это предоставляет нам некоторое указание свободной области при использовании первоначального картографирования.

Далее мы рассмотрим базовую литературу по управлению областью LUT , опишем оптимальный повторный синтез, основанный на SAT , опишем приложение из оптимального подхода повторного синтеза к сетям 4- LUT и предоставим набор результатов. Предоставим заключительные замечания и направления для будущей работы.

Повторный синтез области

Проводя ресинтез области, мы должны взять LUT схему и попытаться сократить число генераторов логических функций LUTs в схеме с сохранением ее первоначального функционирования.

Чем больше LUTs можно исключить, тем больше первоначальная схема будет отличаться от оптимальной конфигурации. Мы упоминали, что сокращение числа LUTs может быть достигнуто ресинтезом меньших подсхем с применением методики «скользящего окна» над большими схемами. Подсхемы, которые мы рассматриваем имеют форму конуса. Поэтому ресинтез нескольких конусов, должен сократить граф полной сети LUT .

Проблема повторного Синтеза

Определим, может ли n -возможный конус содержащий X N - LUTs быть повторно синтезирован в n -возможный конус содержащий X -1 N - LUTs или менее. Этого достигается формированием n - feasible FFC , содержащим меньшее количство LUTs , чем первоначальный конус, выражая FFC как логическое выражение КНФ. Потом, для КНФ выражения составляется таблица истинности переменных первоначального конуса. Если это выражение КНФ выполняется, повторный синтез к новому FFC возможен.

Для иллюстрации этого процесса рассмотрим рисунок 4. Базовый конус (4 a ) состоит из трех 2- LUTs которые реализуют функцию трех переменных. При такой реализации возможно повторно синтезировать 4 a в 4 b , для сохранения одного LUT . Чтобы определить, возможен ли повторный синтез от 4 a к 4 b , 4 b должен быть превращен в выражение КНФ. Как сказано ранее, если выражение истинно, то повторный синтез может быть возможен.

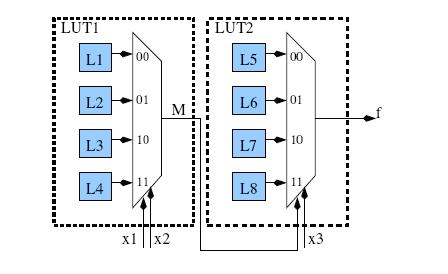
КНФ служит для выражения всех действительных векторов схемы. Например, рассмотрим рисунок 5. Выражение (1) будет удовлетворено, если и только если сигналы A , B , и Z , соответствуют функционированию AND вентиля (например ( A = 0;B = X ; Z =0), ( A = X ;B = 0; Z = 0) или ( A = 1;B = 1; Z = 1)). Таким же образом, выражение 2 будет удовлетворяться только для действительных векторов, например ( A = 1;B = 1; C = 0; Z = 1; Y = 0).

Для проверки повторного синтеза, мы сначала формируем КНФ. Потом, мы накладываем ограничения на входные и выходные переменные в КНФ согласно таблице истинности конуса. Наконец, мы проверяем возможность присваивания используя SAT решатель.

Например, давайте попытаемся спроецировать вторую функцию рисунка 5 на 2х входовой конус. Полагаем, что вход С является конфигурационным битом. Чтобы проверить, что 2х входовая функция f (1; 1)= 1 выполняется, мы определяем, выполняется ли условие F 2( A = 1; B = 1; C ; Z ; Y = 1). Очевидно, это выполняется при C = 1. Однако, это только показывает это f (1; 1)= 1 действительна. Для проверки имеет ли место повторный синтез в схеме выражение КНФ повторяется 2 n раз чтобы сформировать новое выражение КНФ, где n представляет размер конуса. Каждая копия стандартной схемы КНФ представляет один куб в таблице истинности конуса. Опять SAT решатель выполняет проверку новой формулы КНФ на возможность повторного синтеза конуса.

Возвращаясь к базовому примеру LUT (рисунок 4), рассмотрим следующие шаги иллюстрирующие, как происходит преобразование. Рисунок 6 - детальное представление рисунка 4 b с внутренними проводами и конфигурацией вентилей КНФ . В следующих шагах, f представляет собой функцию конуса для повторного синтеза, Xi представляет собой входной вектор x 1 x 2 x 3 = i , и fi = f ( Xi ).

Шаг 1 : Создание выражения КНФ для индивидуальных элементов в схеме повторного синтеза.

Шаг 2: Сформулируем схемное выражение КНФ из выражений (3) (4). Отметим, что выражение (5) зависит от входов схемы и выходов ( x 1 x 2, x 3, f ), внутреннего провода (M), и переменных конфигурации ( L 1- L 8).

Шаг 3: Копия выражения 5 и содержащия согласование входов и выходов для правильного функционирования функции f .

В выражении (6), конфигурируемые биты представляются переменными ( L 1-8) в каждом из Gresynth ( Xi , fi ). тогда как все другие сигналы - представлены уникальными переменными в каждом случае. Это гарантирует, что только одна конфигурация будет существовать для всех кубов таблицы истинности. Наконец, выражение (6) передается в решатель SAT , который вернет истинное значение, если конус соответствует повторному синтезу.

Для простоты, в предыдущем примере мы проигнорировали гибкость трассировки FPGA , которые позволяет входам LUT перемещаться. Это чрезвычайно важно с тех пор как возросло число функций представленных в структуре повторного синтеза. Например, рисунок 7 показывает, как функция от трех переменных может быть преобразована при помощи простой перестановки входов x 1 и x 2.

Распространив рисунок 7 ко всем входным перестановкам увеличивается число функций повторного синтеза представленных n !, где n - размер конуса повторного синтеза. Для того, чтобы представить взаимозаменяемые входы в КНФ, добавлены виртуальные мультиплексоры Рисунок 8. Они виртуальны в смысле, что их не существует в структуре повторного синтеза, но они служат для возможности изменять порядок входов в выражении КНФ.

Перевод на русский язык: Томах Д.В.