Finite state machine

From Wikipedia, the free encyclopedia
(March 2008)

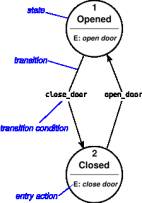
Fig.1 Example of a Finite State Machine

Конечный автомат

Википедия, свободная энциклопедия
(март 2008)

Перевод выполнен Выприцкой П.А. (июнь 2008)

Рис.1 Пример конечного автомата

A finite state machine (FSM) or finite state automaton (plural: automata) or simply a state machine, is a model of behavior composed of a finite number of states, transitions between those states, and actions. A finite state machine is an abstract model of a machine with a primitive internal memory.

Конечный Автомат (КА) или finite state automaton (мн.ч.: automata) или простой автомат - модель поведения, состоящая из конечного ряда состояний, переходов, между этими состояниями, и операций. Конечный автомат – это абстрактная модель механизма с примитивной оперативной памятью.

Concepts and vocabulary

A state stores information about the past, i.e. it reflects the input changes from the system start to the present moment. A transition indicates a state change and is described by a condition that would need to be fulfilled to enable the transition. An action is a description of an activity that is to be performed at a given moment. There are several action types:

Entry action
which is performed when entering the state
Exit action
which is performed when exiting the state
Input action
which is performed depending on present state and input conditions
Transition action
which is performed when performing a certain transition

Понятия и словарь

Текущее состояние автомата дает информацию о предыдущих, т.е. оно отражает входные изменения от системного запуска до текущего момента. Переход показывает изменение состояний и описывает условие, которое должно быть выполнено, чтобы осуществить переход. Операция - описание события, которое должно выполниться в текущий момент. Есть несколько типов операций:

Операция при входе
которая выполняется, на входе в состояние
Операция при выходе
которая выполняется, на выходе из состояния
Входная операция
которая выполняется в зависимости от входных условий состояния
Операция перехода
которая выполняется непосредственно при переходе

A FSM can be represented using a state diagram (or state transition diagram) as in figure 1 above. Besides this, several state transition table types are used. The most common representation is shown below: the combination of current state (B) and condition (Y) shows the next state (C). The complete actions information can be added only using footnotes. An FSM definition including the full actions information is possible using state tables (see also VFSM).

Конечный автомат может быть представлен как диаграмма состояний (или диаграмма переходов) как показано на рисунке 1. Кроме того, используется несколько типов таблиц переходов. Наиболее распространенная запись показана ниже: комбинация текущего состояния (B) и условия (Y) показывает следующее состояние (C). Полная информация об операциях может быть добавлена только используя сноски. Описание конечного автомата, включающее полную информацию об операциях, может быть представлено таблицами состояний.

In addition to their use in modeling reactive systems presented here, finite state automata are significant in many different areas, including electrical engineering, linguistics, computer science, philosophy, biology, mathematics, and logic. A complete survey of their applications is outside the scope of this article. Finite state machines are a class of automata studied in automata theory and the theory of computation. In computer science, finite state machines are widely used in modeling of application behavior, design of hardware digital systems, software engineering, compilers, network protocols, and the study of computation and languages.

Конечные автоматы используются не только в моделировании реагирующих систем, представленных здесь, но и во многих других областях, в том числе: электротехника, лингвистика, информатика, философия, биология, математика и логика. Полный обзор их применения не входит в состав этой статьи. КА - класс автоматов, изучаемых в теории автоматов и теории вычисления. В информатике конечные автоматы широко используются в моделировании поведения приложений, проектировании аппаратных цифровых систем, разработке программного обеспечения, компиляторов, сетевых протоколов, и изучении вычисления и языков.

Classification

There are two different groups: Acceptors/Recognizers and Transducers.

Acceptors and recognizers

Fig. 2 Acceptor FSM: parsing the word "nice"

Acceptors and recognizers (also sequence detectors) produce a binary output, saying either yes or no to answer whether the input is accepted by the machine or not. All states of the FSM are said to be either accepting or not accepting. At the time when all input is processed, if the current state is an accepting state, the input is accepted; otherwise it is rejected. As a rule the input are symbols (characters); actions are not used. The example in figure 2 shows a finite state machine which accepts the word "nice". In this FSM the only accepting state is number 7.

Классификация

Есть две различных группы: Приемник/Устройства распознавания и Преобразователи.

Приемники и устройства распознавания

Рис. 2 Распознающий конечный автомат: грамматический анализ слова "nice"

Преобразователи и устройства (также датчики) распознавания выдают бинарный ответ да или нет, принимает ли ввод машина или нет. Любое состояние конечного автомата говорит о принятии или непринятии условия. В тот момент, когда все входные данные обработаны, если текущее состояние – принимающее - ввод принят; иначе отвергнут. Как правило, если на входе символы, то операции не используются. Пример на рисунке 2 показывает конечный автомат, который принимает слово "nice". В этом конечном автомате принимающее состояние – состояние с номером 7.

The machine can also be described as defining a language, which would contain every word accepted by the machine but none of the rejected ones; we say then that the language is accepted by the machine. By definition, the languages accepted by FSMs are the regular languages - that is, a language is regular if there is some FSM that accepts it.

Автомат может также быть описан как язык, каждое слово которого принимается автоматом и ни одно не отвергается; тогда можно сказать, что язык принимается автоматом. По определению, языки, принимаемые конечными автоматами, - регулярные языки.

Start state

The start state is usually shown drawn with an arrow "pointing at it from nowhere" (Sipser (2006) p.34).

Accept state

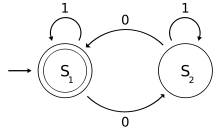
Fig. 3: A finite state machine that determines if a binary number has an odd or even number of 0s.

Начальное состояние

Начальное состояние обычно показывается со стрелкой, "направленной в него из ниоткуда" (Sipser (2006) p.34).

Состояние ввода

Рис. 3: КА определения четности количества 0 в двоичном числе.

An accept state (sometimes referred to as an accepting state) is a state at which the machine has successfully performed its procedure. It is usually represented by a double circle.

An example of an accepting state appears on the left in this diagram of a deterministic finite automaton (DFA) which determines if the binary input contains an even number of 0s.

S1 (which is also the start state) indicates the state at which an even number of 0s has been input and is therefore defined as an accepting state. This machine will give a correct end state if the binary number contains an even number of zeros including a string with no zeros. Examples of strings accepted by this DFA are epsilon (the empty string), 1, 11, 11..., 00, 010, 1010, 10110 and so on.

Состояние ввода (иногда понимается как принимающее состояние) - состояние, в котором машина успешно выполнила свою процедуру. Это обычно отображается двойным кругом.

Пример принимающего состояния показан слева в этой диаграмме Детерминированного Конечного Автомата (ДКА), который определяет содержит ли двоичное вводимое число очередной ряд 0.

S1 (которое является также начальным состоянием) указывает состояние, в котором ряд 0 были входными, и поэтому оно определяется как принимающее состояние. Этот автомат даст правильное конечное состояние, если двоичное число содержит четное число нолей, или в строке нет нулей. Примеры строк, принятых этим ДКА - эпсилон (пустая строка), 1, 11, 11..., 00, 010, 1010, 10110, и так далее.

Transducers

Transducers generate output based on a given input and/or a state using actions. They are used for control applications and in the field of computational linguistics. Here two types are distinguished:

Преобразователи

Преобразователи генерируют выходные данные и/или состояние по полученным входным данным используя операции. Они используются для контроля приложений и в сфере вычислительной лингвистики. Существует 2 выдающихся типа автоматов:

Moore machine

The FSM uses only entry actions, i.e. output depends only on the state. The advantage of the Moore model is a simplification of the behaviour. The example in figure 1 shows a Moore FSM of an elevator door. The state machine recognizes two commands: "command_open" and "command_close" which trigger state changes. The entry action (E:) in state "Opening" starts a motor opening the door, the entry action in state "Closing" starts a motor in the other direction closing the door. States "Opened" and "Closed" don't perform any actions. They signal to the outside world (e.g. to other state machines) the situation: "door is open" or "door is closed".

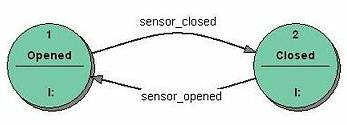
Fig. 4 Transducer FSM: Mealy model example

Автомат Мура

КА использует только операцию входа, т.е. выход зависит только от состояния. Преимущество модели Мура - упрощение поведения. Пример на рисунке 1 показывает КА Мура управления дверью лифта. КА распознает две команды: "command_open" и "command_close", и хранит установленные изменения. Операция (E:) входа в состояние "Opening" запускает двигатель, открывающий дверь, операция входа в состояние "Closing" запускает двигатель в другом направлении - закрытие двери. Состояния "Opened" и "Closed"не выполняют никаких действий. Они сигнализируют внешнему миру (например, к другим КА) положение: "дверь открыта" или "дверь закрыта".

Рис. 4 Преобразователь КА: пример модели Мили

Mealy machine

The FSM uses only input actions, i.e. output depends on input and state. The use of a Mealy FSM leads often to a reduction of the number of states. The example in figure 4 shows a Mealy FSM implementing the same behaviour as in the Moore example (the behaviour depends on the implemented FSM execution model and will work e.g. for virtual FSM but not for event driven FSM). There are two input actions (I:): "start motor to close the door if command_close arrives" and "start motor in the other direction to open the door if command_open arrives".

Автомат Мили

КА использует только входные операции, т.е. выход зависит от входа и состояния. Использование КА Мили часто приводит к сокращению числа состояний. Пример на рисунке 4 показывает КА Мили, осуществляющий то же поведение как в примере Мура (поведение зависит от реализации КА и будут работать например для виртуального КА, но не для случая управляемого КА). Есть два входных действия (I:): "запустите двигатель, чтобы закрыть дверь, если получено command_close" и " запустите двигатель в другом направлении, чтобы открыть дверь, если получено command_open".

In practice mixed models are often used.

More details about the differences and usage of Moore and Mealy models, including an executable example, can be found in the external technical note "Moore or Mealy model?"

A further distinction is between deterministic (DFA) and non-deterministic (NDFA, GNFA) automata. In deterministic automata, for each state there is exactly one transition for each possible input. In non-deterministic automata, there can be none or more than one transition from a given state for a given possible input. This distinction is relevant in practice, but not in theory, as there exists an algorithm which can transform any NDFA into an equivalent DFA, although this transformation typically significantly increases the complexity of the automaton.

The FSM with only one state is called a combinatorial FSM and uses only input actions. This concept is useful in cases where a number of FSM are required to work together, and where it is convenient to consider a purely combinatorial part as a form of FSM to suit the design tools.

На практике часто используются смешанные модели.

Больше деталей об отличиях и использовании моделей Мура и Мили, в том числе выполнимый пример, могут быть найдены во внешнем техническом примечании "Модель Мили или Мура?"

Дальше рассмотрим различия между детерминированными (ДКА) и недетерминированными (НДКА) автоматами. В детерминированных автоматах, для каждого состояния всегда есть только один переход для каждого возможного входного условия. В недетерминированных автоматах, может не быть вообще или быть более одного перехода из текущего состояния для каждого возможного входного условия. Это различие имеет смысл на практике, но не теоретически, так как существует алгоритм, преобразования любого НДКА в эквивалентный ДКА, хотя это преобразование обычно значительно увеличивает сложность автомата.

КА только с одним состоянием называются комбинаторным КА и используют только входные действия. Это понятие полезно в случаях, когда несколько КА должны работать совместно, и когда удобно рассматривать исключительно комбинаторную часть как форму КА, чтобы удовлетворять инструментам проекта.

FSM logic

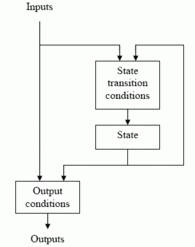
Fig. 5 FSM Logic

The next state and output of an FSM is a function of the input and of the current state. The FSM logic is shown in Figure 5.

Логика КА

Рис. 5 Логика КА

Следующее состояние и выход из КА являются функцией входа и текущего состояния. Логика КА показана на рисунке 5.

Mathematical model

Depending on the type there are several definitions. An acceptor finite-state machine is a quintuple (Σ,S,s0,δ,F), where:

Σ is the input alphabet (a finite, non-empty set of symbols).
S is a finite, non-empty set of states.
s0 is an initial state, an element of S. In a Nondeterministic finite state machine, s0 is a set of initial states.
δ is the state-transition function.
F is the set of final states, a (possibly empty) subset of S.

Математическая модель

В зависимости от типа есть несколько определений. КА приемник состоит из пяти частей (Σ,S,s0,δ,F), где:

Σ - входной алфавит (конечное, не пустое, множество символов).
S - конечное, не пустое, множество состояний.
s0 - начальное состояние, элемент множества S. В НДКА s0 - множество начальных состояний.
δ - функция перехода состояния.
F - множество конечных состояний, (может быть пустым) подмножество S.

A transducer finite-state machine is a sextuple (Σ,Γ,S,s0,δ,ω), where:

Σ is the input alphabet (a finite non empty set of symbols).
Γ is the output alphabet (a finite, non-empty set of symbols).
S is a finite, non-empty set of states.
s0 is the initial state, an element of S. In a Nondeterministic finite state machine, s0 is a set of initial states.
δ is the state-transition function.
ω is the output function.

КА преобразователь состоит из шести частей (Σ,Γ,S,s0,δ,ω), где:

Σ - входной алфавит (конечное, не пустое, множество символов).
Г - выходной алфавит (конечное, не пустое, множество символов).
S - конечное, не пустое, множество состояний.
s0 - начальное состояние, элемент множества S. В НДКА s0 - множество начальных состояний.
δ - функция перехода состояния.
ω - выходная функция.

If the output function is a function of a state and input alphabet () that definition corresponds to the Mealy model, and can be modelled as a Mealy machine. If the output function depends only on a state () that definition corresponds to the Moore model, and can be modelled as a Moore machine. A finite-state machine with no output function at all is known as a semiautomaton or transition system.

Если выходная функция является функцией состояний и входного алфавита, то это определение соответствует модели Мили, и может моделироваться как автомат Мили. Если выходная функция зависит только от состояния, то это определение соответствует модели Мура и может моделироваться как автомат Мура. КА без выходной функции вообще известна как полуавтомат или система переходов.

Optimization

Optimizing an FSM means finding the machine with the minimum number of states that performs the same function. One possibility is by using an Implication table or the Moore reduction procedure. Another possibility is bottom-up algorithm for Acyclic FSAs.

Оптимизация

Оптимизация КА подразумевает поиск автомата с минимальным числом состояний, выполняющего те же функции. Один из способов - это используя таблицу импликации или процедуру оптимизации Мура. Второй способ - восходящий алгоритм для Ациклического КА.

Implementation

In a digital circuit, an FSM may be built using a programmable logic device, a programmable logic controller, logic gates and flip flops or relays. More specifically, a hardware implementation requires a register to store state variables, a block of combinational logic which determines the state transition, and a second block of combinational logic that determines the output of an FSM. One of the classic hardware implementations is the Richard's Controller.

Реализация

Цифровая схема КА может быть сформирована, используя программируемое логическое устройство, программируемые логические контроллеры, логические защелки и триггеры или реле. Более подробно, аппаратная реализация требует регистр для хранения переменных состояний, блок комбинационной логики, который определяет изменение состояний, и второй блок комбинационной логики, который определяет выход из КА. Одна из классических аппаратных реализаций – Контроллер Ричарда.

Software applications

The following concepts are commonly used to build software applications with finite state machines:

event driven FSM
virtual FSM (VFSM)
Automata-Based Programming

ПО

Следующие понятия обычно используются для создания программного обеспечения с КА:

событийно управляемый КА
виртуальный КА (ВКА)
Программирование автоматов

History

This section does not cite any references or sources. (July 2007)

Starting in the 1970s, Leslie Lamport, an early leader within the distributed systems research community, used finite state machines as the basis for an algorithm he called state machine replication. In this approach, a deterministic computer program or service is replaced with a set of replicas that use some form of atomic broadcast to perform operations in a manner tolerant of failures.

История

В этой секции не цитируются никакие ссылки или источники. (Июль 2007)

Начиная с 1970-х, Лесли Лампорт, один из первых, кто начал исследования распределенных систем, использовал КА в качестве основы для алгоритма, который он вызывал автоматом дублирования. При таком подходе, определяющая компьютерная программа или служба заменяется набором точных копий, которые используют некоторую форму простейшей передачи, чтобы сделать выполнение операций устойчивым по отношению к сбоям.