| Биография | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание | ДонНТУ | Портал магистров ДонНТУ |
Источник: Материалы студенческой научно-практической конференции,посвященной Дню науки на кафедре прикладной математики и информатики, ДонНТУ, 2008.
Применение теории нечетких множеств к задачам анализа риска инвестиций
Зайцева А.С.
Донецкий национальный технический университет
Управление финансовыми активами преследует цель достижения определенного экономического эффекта в будущем времени. Будущее неясно, и управление протекает в условиях неопределенности относительно будущего состояния как самих финансовых активов, так и их экономического окружения. Неопределенность порождает риск неэффективного управления - такого, что намеченные цели управления не достигаются. Например, решение об инвестициях, первоначально признанное экономически обоснованным, может перестать быть таковым вследствие ухудшения рыночной конъюнктуры (снижение фактической выручки по сравнению с плановой, или рост затрат по сравнению с планом, или то и другое). Поэтому задача минимизации риска неэффективного управления финансами сводится к задаче всемерной борьбы с неопределенностью.
Исторически первым способом учета неопределенности было изобретение вероятностей. Успешное применение вероятностных методов в статистике конца XIX века (при исследовании массовых и статистически однородных демографических процессов) сделало методы теории вероятностей широко распространенными во всех сферах жизни, особенно с развитием технической кибернетики во второй половине XX века. Использование вероятностей при учете случайности, неопределенности, ожидаемости событий приобрело эксклюзивный характер. Наиболее оправданным такое применение оказалось там, где речь шла об однородных событиях массового характера, а именно - в теории массового обслуживания и в технической теории надежности.
Однако, начиная с 50-х годов, в академической науке появились работы, ставящие под сомнение тотальную применимость вероятностной теории к учету неопределенности. Авторы этих работ закономерно отмечали, что классическая вероятность аксиоматически определена как характеристика генеральной совокупности статистически однородных случайных событий. В том случае, если статистической однородности нет, то применение классических вероятностей в анализе оказывается незаконным.
Реакцией на эти вполне обоснованные замечания стали фундаментальные работы Сэвиджа, Пойа, Кайберга, Фишберна, де Финетти и других, где обосновывалось введение неклассических вероятностей, не имеющих частотного смысла, а выражающих познавательную активность исследователя случайных процессов или лица, вынужденного принимать решения в условиях дефицита информации. Так появились субъективные (аксиологические) вероятности.
Однако появление неклассических вероятностей не было единственной реакцией на возникшую проблему. Необходимо отметить также всплеск интереса к минимаксным подходам, а также зарождение теории нечетких множеств. Основы теории нечетких множеств заложены в фундаментальных работах Лофти Заде. Первоначальным замыслом этой теории было построить функциональное соответствие между нечеткими лингвистическими описаниями (типа “высокий”, “теплый” и т.д.) и специальными функциями, выражающими степень принадлежности значений измеряемых параметров (длины, температуры, веса и т.д.) упомянутым нечетким описаниям.
Впоследствии диапазон применимости теории нечетких множеств существенно расширился. Сам Заде определил нечеткие множества как инструмент построения теории возможностей. Следующим достижением теории нечетких множеств является введение в обиход так называемых нечетких чисел как нечетких подмножеств специализированного вида, соответствующих высказываниям типа “значение переменной примерно равно а”.
Прикладные результаты теории нечетких множеств не заставили себя ждать. Для примера: сегодня зарубежный рынок так называемых нечетких контроллеров (разновидность которых установлена даже в стиральных машинах широко рекламируемой марки LG) обладает емкостью в миллиарды долларов. Нечеткая логика, как модель человеческих мыслительных процессов, встроена в системы искусственного интеллекта и в автоматизированные средства поддержки принятия решений (в частности, в системы управления технологическими процессами).
В случае применения нечетких чисел к прогнозу параметров от ЛПР требуется не формировать точечные вероятностные оценки, а задавать расчетный коридор значений прогнозируемых параметров. Тогда ожидаемый эффект оценивается экспертом так же, как нечеткое число со своим расчетным разбросом (степенью нечеткости). Здесь возникают инженерные преимущества метода, основанного на нечеткостях, т.к. исследователь оперирует не косвенными оценками (куда относим и вероятности), а прямыми проектными данными о разбросе параметров, что есть хорошо известная практика интервального подхода к проектным оценкам.
Что же касается оценки риска принятия решения в условиях неопределенности, то вероятностные и нечетко-множественные методы предоставляют исследователю здесь примерно одинаковые возможности. Степень устойчивости решений верифицируется в ходе анализа чувствительности решения к колебаниям исходных данных, и эта устойчивость может оцениваться аналитически.
Инвестиционный проект предполагает планирование во времени трех основных денежных потоков: потока инвестиций, потока текущих (операционных) платежей и потока поступлений. Ни поток текущих платежей, ни поток поступлений не могут быть спланированы вполне точно, поскольку нет и не может быть полной определенности относительно будущего состояния рынка. Цена и объемы реализуемой продукции, цены на сырье и материалы и прочие денежно-стоимостные параметры среды по факту их осуществления в будущем могут сильно разниться с предполагаемыми плановыми значениями, которые оцениваются с позиций сегодняшнего дня.
Неустранимая информационная неопределенность влечет столь же неустранимый риск принятия инвестиционных решений. Всегда остается возможность того, что проект, признанный состоятельным, окажется de-facto убыточным, поскольку достигнутые в ходе инвестиционного процесса значения параметров отклонились от плановых, или же какие-либо факторы вообще не были учтены. Инвестор никогда не будет располагать всеобъемлющей оценкой риска, так как число разнообразий внешней среды всегда превышает управленческие возможности принимающего решения лица, и обязательно найдется слабоожидаемый сценарий развития событий (любая катастрофа, к примеру), который, будучи неучтен в проекте, тем не менее, может состояться и сорвать инвестиционный процесс. В то же время инвестор обязан прилагать усилия по повышению уровня своей осведомленности и пытаться измерять рискованность своих инвестиционных решений как на стадии разработки проекта, так и в ходе инвестиционного процесса.
В литературе по инвестиционному анализу хорошо известна формула чистой современной ценности инвестиций (NPV - Net Present Value). Возьмем один важный частный случай оценки NPV, который и будем использовать в дальнейшем рассмотрении:
1. Все инвестиционные поступления приходятся на начало инвестиционного процесса.
2. Оценка ликвидационной стоимости проекта производится post factum, по истечении срока жизни проекта.
Тогда соотношение для NPV имеет следующий вид:
,
где
I - стартовый объем инвестиций,
N - число плановых интервалов (периодов) инвестиционного процесса, соответствующих сроку жизни проекта,
D Vi - оборотное сальдо поступлений и платежей в i-ом периоде,
ri - ставка дисконтирования, выбранная для i-го периода с учетом оценок ожидаемой стоимости используемого в проекте капитала (например, ожидаемая ставка по долгосрочным кредитам),
C - ликвидационная стоимость чистых активов, сложившаяся в ходе инвестиционного процесса (в том числе остаточная стоимость основных средств на балансе предприятия).
Инвестиционный проект признается эффективным, когда NPV больше определенного проектного уровня G (в самом распространенном случае G = 0).
Замечания.
1. NPV оценивается в постоянных (реальных) ценах.
2. Ставка дисконтирования планируется такой, что период начислений процентов на привлеченный капитал совпадает с соответствующим периодом инвестиционного процесса.
3. (N+1
)-й интервал не относится к сроку жизни проекта, а выделен в модели для фиксации момента завершения денежных взаиморасчетов всех сторон в инвестиционном процессе (инвесторов, кредиторов и дебиторов) по кредитам, депозитам, дивидендам и т.д., когда итоговый финансовый результат проекта сделается однозначным.Если все параметры в формуле обладают “размытостью”, т.е. их точное планируемое значение неизвестно, тогда в качестве исходных данных уместно использовать так называемые треугольные нечеткие числа с функцией принадлежности следующего вида (рис. 1).
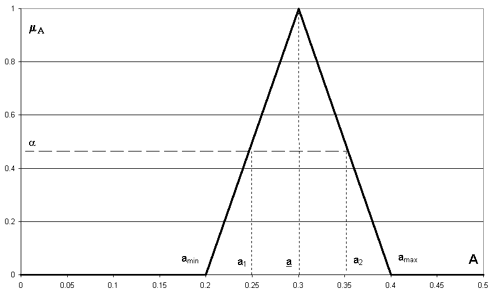
Рис. 1. Функция принадлежности треугольного нечеткого числа
АЭти числа моделируют высказывание следующего вида: “параметр А приблизительно равен 
и однозначно находится в диапазоне [amin, amax]”.
В общем случае под нечетким числом понимается нечеткое подмножество универсального множества действительных чисел, имеющее нормальную и выпуклую функцию принадлежности [6]. Такое описание позволяет разработчику инвестиционного проекта взять в качестве исходной информации интервал параметра
[amin, amax] и наиболее ожидаемое значение, и тогда соответствующее треугольное число 
построено. Далее будем называть параметры
значимыми точками треугольного нечеткого числа 
. Вообще говоря, выделение трех значимых точек исходных данных весьма распространено в инвестиционном анализе. Часто этим точкам сопоставляются субъективные вероятности реализации соответствующих (“пессимистического”, “нормального” и “оптимистического”) сценариев исходных данных.
Теперь можно задать следующий набор нечетких чисел для анализа эффективности проекта:
- инвестор не может точно оценить, каким объемом инвестиционных ресурсов он будет располагать на момент принятия решения;
- инвестор не может точно оценить стоимость капитала, используемого в проекте (например, соотношение собственных и заемных средств, а также процент по долгосрочным кредитам);
- инвестор прогнозирует диапазон изменения денежных результатов реализации проекта с учетом возможных колебаний цен на реализуемую продукцию, стоимости потребляемых ресурсов, условий налогообложения, влияния других факторов;
- инвестор нечетко представляет себе потенциальные условия будущей продажи действующего бизнеса или его ликвидации;
- инвестор нечетко представляет себе критерий, по которому проект может быть признан эффективным, или не до конца отдает себе отчет в том, что можно будет понимать под “эффективностью” на момент завершения инвестиционного процесса.
Замечания.
1. В том случае, если какой-либо из параметров
известен вполне точно или однозначно задан, то нечеткое число вырождается в действительное число А с выполнением условия
. При этом существо метода остается неизменным.
2. В отношении вида
. Инвестор, выбирая ожидаемую оценку 
, руководствуется, возможно, не только тактическими, но и стратегическими соображениями. Так, он может позволить проекту быть даже несколько убыточным, если этот проект диверсифицирует деятельность инвестора и повышает надежность его бизнеса. Как вариант: инвестор реализует демпинговый проект, компенсацией за временную убыточность станет захват рынка и сверхприбыль, но инвестор хочет отсечь сверхнормативные убытки на той стадии, когда рынок уже будет переделен в его пользу. Или наоборот: инвестор идет на повышенный риск во имя прироста средневзвешенной доходности своего бизнеса.
Таким образом, задача инвестиционного выбора в приведенной выше постановке есть процесс принятия решения в расплывчатых условиях, когда решение достигается слиянием целей и ограничений.
Чтобы преобразовать формулу расчета NPV к виду, пригодному для использования нечетких исходных данных, воспользуемся сегментным способом.
Часто оказывается возможным привести
к треугольному виду, ограничиваясь расчетами по значимым точкам нечетких чисел исходных данных. Это позволяет рассчитывать все ключевые параметры в оценке степени риска не приближенно, а на основе аналитических соотношений. Это будет показано на расчетном примере в конце настоящей работы.
Перейдем к оценке собственно риска инвестиций. На рис. 2 представлены функции принадлежности и критериального значения .
Рис. 2. Функции принадлежности
NPV и GТочкой пересечения этих двух функций принадлежности является точка с ординатой
a 1. Выберем произвольный уровень принадлежности a и определим соответствующие интервалы [NPV1, NPV2] и [G1, G2]. При a > a 1 NPV1 > G2, интервалы не пересекаются, и уверенность в том, что проект эффективен, стопроцентная, поэтому степень риска неэффективности инвестиций равна нулю. Уровень a 1 уместно назвать верхней границей зоны риска. При 0 £ a £ a 1 интервалы пересекаются. На рис. 3 показана заштрихованная зона неэффективных инвестиций, ограниченная прямыми G = G1, G = G2, NPV = NPV1, NPV = NPV2 и биссектрисой координатного угла G = NPV.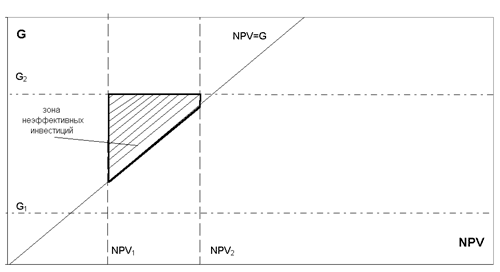
Рис. 3. Фазовое пространство
(NPN, G)Взаимные соотношения параметров
G1,2 и NPV1,2 дают следующий расчет для площади заштрихованной плоской фигуры:
Поскольку все реализации
(NPV, G) при заданном уровне принадлежности a равновозможны, то степень риска неэффективности проекта j (a ) есть геометрическая вероятность события попадания точки (NPV, G) в зону неэффективных инвестиций:
,
где
Sa оценивается по вышеуказанной формуле.Тогда итоговое значение степени риска неэффективности проекта:
Выводы
Подход, основанный на нечеткостях, преодолевает недостатки вероятностного и минимаксного подходов, связанные с учетом неопределенности. Во-первых, здесь формируется полный спектр возможных сценариев инвестиционного процесса. Во-вторых, решение принимается не на основе двух оценок эффективности проекта, а по всей совокупности оценок. В-третьих, ожидаемая эффективность проекта не является точечным показателем, а представляет собой поле интервальных значений со своим распределением ожиданий, характеризующимся функцией принадлежности соответствующего нечеткого числа. А взвешенная полная совокупность ожиданий позволяет оценить интегральную меру ожидания негативных результатов инвестиционного процесса, т.е. степень инвестиционного риска.