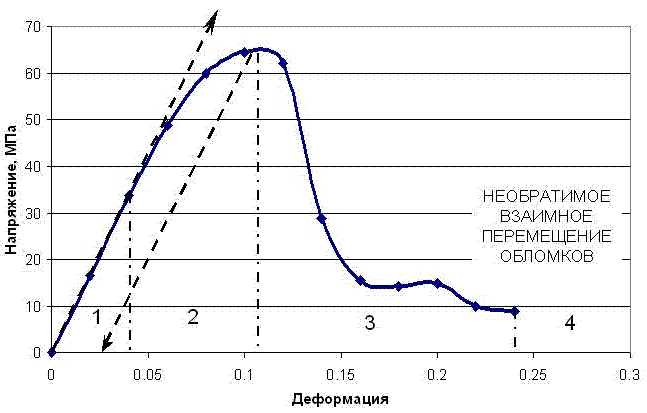
Рисунок 1 - Кривая деформирования участка массива горных пород с учетом всех основных нелинейных этапов
Источник: Методические указания по курсу "Материалознавство", 2005

Рисунок 1 - Кривая деформирования участка массива горных пород с учетом всех основных нелинейных этапов
На третьем этапе деформирования породы происходит резкое уменьшение напряжений при продолжающейся ее деформации. Этот этап называют запредельным, так как происходит исчерпание предела прочности породы. Типичным примером запредельного деформирования массива является отжим краевой части пласта.
Последним характерным этапом условного деформирования массива после его разрушения можно считать необратимое взаимное перемещение обломков. Такое перемещение происходит при обрушении кровли, перемещении закладки в выработанное пространство, уплотнении обрушенных пород и т.д. Важно отметить, что при решении практических задач горного дела четвертый этап перемещения обломков или частиц пород часто рассматривается как продолжение процесса необратимого деформирования массива в целом.Еще одним специфическим нелинейным деформированием обладают породы, склонные к ползучести во времени под действием постоянной нагрузки (рис. 2). Наиболее типичным примером временнoй ползучести горного массива является деформирование камер и потолочин месторождений соли без разрушения их сплошности.
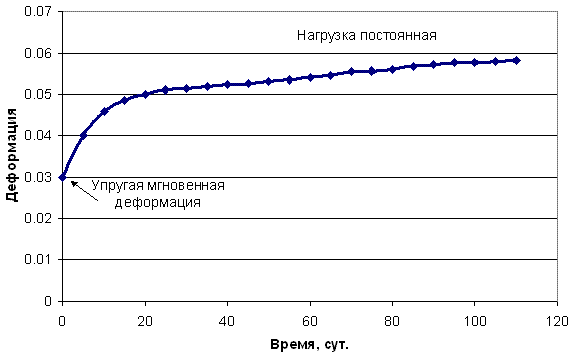
Рисунок 2 - Кривая ползучести горной породы как пример нелинейного ее деформирования
Следует отметить, что большинство нелинейных методов механики деформируемого тела основаны на вышеописанном алгоритме, который разработан для упругого механизма деформирования. Учет нелинейности осуществляется за счет искусственных приемов, некоторые из них описываются далее.
Основой для учета нелинейного дефомирования массива горных пород является его деформационная характеристика. Нелинейность деформирования массива на этапах 2 и 3 имитируют путем многократного или пошагового расчета напряжено-деформированного состояния при изменении модуля деформации рассматриваемого массива. На рис. 3 показан прием учета нелинейности деформирования, основанный на переменном модуле деформации. Смысл такого приема заключается в следующем. На начальном этапе расчета определяют напряжения и деформации во всех расчетных точках модели. Затем проверяют адекватность величин напряжений и деформаций по экспериментальной (или априорно заданной) деформационной кривой. В тех точках расчетной области, где соотношения между напряжениями и деформациями не ложатся на экспериментальную деформационную кривую, изменяют (как правило, уменьшают) модуль деформации таким образом, чтобы полученные напряжения соответствовали деформациям и пересчитывают все распределение напряжений в модели заново. В процессе приведения напряжений и деформаций в экспериментально установленное соответствие приходится заменять отрезок деформационной кривой прямым отрезком, который пересекает ее в точке, где наблюдается соответствие напряжений и деформаций. По этой причине такой подход получил название метода секущих модулей. Недостатком такого метода является необходимость пересчета всей матрицы жесткости в случае использования метода конечных элементов, что увеличивает время расчета. При применении других методов расчета необходимо пересчитывать характеристики, аналогичные тем, которые составляют матрицу жесткости в МКЭ. Кроме того, сходимость решения получить удается не всегда. Другими словами при каждом новом пересчете напряженного состояния модели расхождение между напряжениями и деформациями в тех точках, где предел упругости был превышен не только не уменьшается, но часто и растет.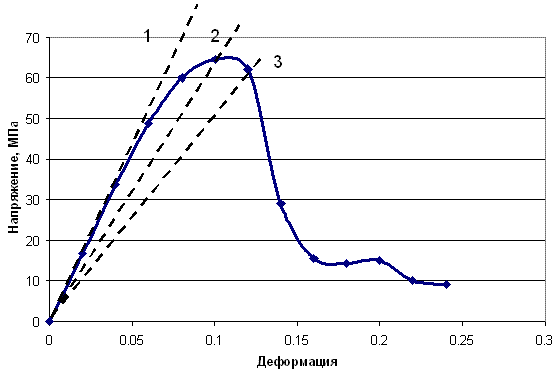
Рисунок 3 - Учет нелинейности деформирования породы методом переменных секущих модулей
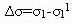 . В узел, где обнаружена такая невязка, вводят компоненты сил, пропорциональные полученной невязке с обратным знаком и тем самым приводят в соответствие величины напряжений и деформаций согласно экспериментальной нелинейной зависимости. Такой подход назван методом начальных напряжений. Поскольку такая корректировка производится в нескольких узлах сразу, сходимость решения достигается постепенно, в течение несколько итераций. Важно, что при этом матрица жесткости не пересчитывается, что ускоряет время решения задачи.
. В узел, где обнаружена такая невязка, вводят компоненты сил, пропорциональные полученной невязке с обратным знаком и тем самым приводят в соответствие величины напряжений и деформаций согласно экспериментальной нелинейной зависимости. Такой подход назван методом начальных напряжений. Поскольку такая корректировка производится в нескольких узлах сразу, сходимость решения достигается постепенно, в течение несколько итераций. Важно, что при этом матрица жесткости не пересчитывается, что ускоряет время решения задачи.
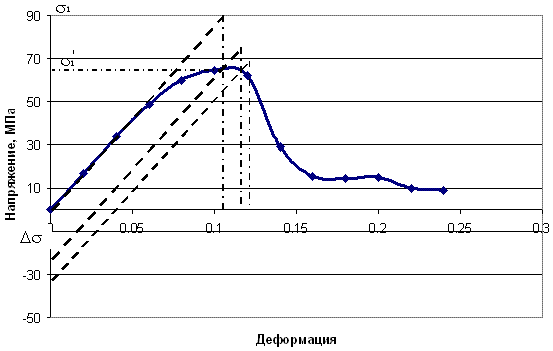
Рисунок 4 - Иллюстрация метода начальных напряжений, обслуживающего нелинейность деформационной характеристики
Существует большое количество приемов для учета нелинейного деформирования среды. Однако следует оговориться, что для моделирования процессов, протекающих на всех этапах, включая четвертый, необходимо применение принципиально иных методов.