 (1)
(1)
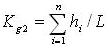 (2)
(2)
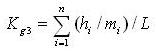 (3)
(3)
 (1)
(1)
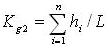 (2)
(2)
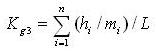 (3)
(3)
С целью изучения отношения между индексом ошибки туннеля и индексом ошибки рабочего места, мы используем двадцать пять образцов рабочих материалов взятых в горнодобывающем бюро регрессии Pingdingshan, чтобы провести по регрессии при степенной функции, экспоненциальной функции, обратном индексе, логарифмической функции, функции формы линии. В таблице 1 приведены наиболее достоверные результаты.
|
Индекс ошибки рабочего места |
Индекс ошибки туннеля |
Прогнозируемый индекс ошибки туннеля |
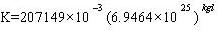 |
||
| (r=0.558) | ||
 |
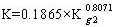 |
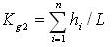 |
| (r=0.8661) | ||
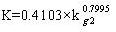 |
||
| (r=0.8378) |
|
Правило регрессионного анализа |
Уравнения регрессии |
Относительная предсказанная ошибка (в среднем три поверхности) |
| Наименьший квадрат | 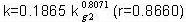 |
43.12% |
| Грубая регрессия | ||
| Нет выбора | 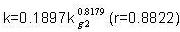 |
38.31% |
| Выбор из 1 |  |
34.39% |
| Выбор из 4 | 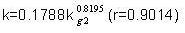 |
29.32% |
| Выбор из 7 | 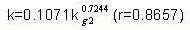 |
22.17% |
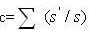 , s' - площадь тонкого пласта, s - площадь рабочей поверхности. Исследуя туннель, проводим измерение длины туннеля по тонкому угольному поясу и общей длины туннеля L. Предположим, что Kc=i/L,
, s' - площадь тонкого пласта, s - площадь рабочей поверхности. Исследуя туннель, проводим измерение длины туннеля по тонкому угольному поясу и общей длины туннеля L. Предположим, что Kc=i/L, 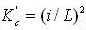 , тогда мы можем получить истинный индекс разрушения C в тонком пласту, строя статистическое отношение между C и Kc или C и K'c . Мы собрали двадцать пять образцов материалов рабочих поверхностей, их индексы разрушения в горнодобывающем бюро Pingdingshan. Проделан статистический и регрессионный прогноз отдельно для C - Kc и C - K'c. Списки результатов в таблице 3 и фактический результат прогноза таблица 4.
, тогда мы можем получить истинный индекс разрушения C в тонком пласту, строя статистическое отношение между C и Kc или C и K'c . Мы собрали двадцать пять образцов материалов рабочих поверхностей, их индексы разрушения в горнодобывающем бюро Pingdingshan. Проделан статистический и регрессионный прогноз отдельно для C - Kc и C - K'c. Списки результатов в таблице 3 и фактический результат прогноза таблица 4.
|
Правило регрессионного анализа |
Уравнения регрессии |
Относительная предсказанная ошибка (в среднем пять поверхностей) |
| Наименьший квадрат | 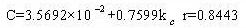 |
9.36% |
| Грубая регрессия | ||
| Нет выбора | 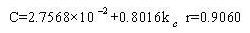 |
9.00% |
| Выбор из 3 | 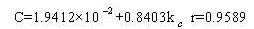 |
9.25% |
| Выбор из 4 | 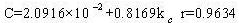 |
9.05% |
| Выбор из 6 |  |
9.61% |
|
Правило регрессионного анализа |
Уравнения регрессии |
Относительная предсказанная ошибка (в среднем пять поверхностей) |
| Наименьший квадрат | C=0.1189+0.9278K'c; r=0.8059 | 12.32% |
| Грубая регрессия | ||
| Нет выбора | C=0.1131+0.9936K'c; r=0.8482 | 12.02% |
| Выбор из 1 | C=0.1073+1.0911K'c; r=0.8906 | 11.85% |
| Выбор из 3 | C=0.1068+1.0938K'c; r=0.9192 | 11.82% |
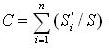 (4)
(4)
После исследований вокруг рабочей поверхности туннеля, имеют место изменения высоты кровли по длине туннеля. Непосредственно для частичных сгибов можно выбрать, сгиб, который исчезает в рабочей поверхности, тогда можно получать результаты в туннеле длиной L и высотой h и сгиб, который проходит через оценивание. Согласно вышеупомянутому статистическому отношению для установленных S' и L и h, извлекают индекс разрушения сгиба С. Согласно Da Zhuang шестнадцать образцов материалов шахтных рабочих поверхностей, получают S' и L и h, большинство из которых превосходят статистические отношения, см. таблицу 5 и таблицу 6.
|
Правило регрессионного анализа |
Уравнения регрессии |
Относительная предсказанная ошибка (в среднем четыре поверхности) |
| Наименьший квадрат | S' =-2207.198+71.428L+79.638h r=0.768 | 36.07% |
| Грубая регрессия | ||
| Нет выбора | S' =-2306.141+70.924L+86.969h r=0.77 | 35.29% |
| Выбор из 2 | S' =-6709.664+70.068L+237.477h r=0.768 | 26.77% |
| Выбор из 3 | S' =-10776.3+77.478L+307.437h r=0.768 | 28.80% |
|
Правило регрессионного анализа |
Наименьший квадрат; Уравнения регрессии |
Относительная предсказанная ошибка (в среднем четыре поверхности |
| x=L | S' =-812.622+70.463x; r=0.768 | 37.03% |
| x=Lh | S' =10497+2.570x; r=0.771 | 28.70% |
| x=L | S' =10370.52+7.394?10x; r=0.683 | 24.95% |
| x=L | S' =1221.295+118.128x r=0.768 | 25.29% |
S'=-10776.3+77.478L+307.437h (5)
S'=10497.52+2.57(Lh) (6)
[1] Wang Yunjia, Jiao Baowen. Оптимальная форма рабочей ошибки вида поврежденного коэффициента и его статистическое предсказание. Угольная геология и исследования, 1996,(2): 23-27(на китайском языке)
[2] Wang Yunjia, Huang bolu. Исследования по применению статистики в горной промышленности. Разработки всемирной угольной технологии, 1993, (8):31-35(на китайском языке)
[3] Wu Liangcai. Исследование оценки условия и предсказания вида индекса рабочего производства в горной промышленности. Тезисы. Пекин: китайский университет горной промышленности и технологии, 1995(на китайском языке)
[4] Wang Rongxin. Математическая статистика. Xi’an: Xi’an Jiaotong Университетская пресса, 1989 (на китайском языке)